Анализ вариационных рядов, показатели дифференциации и концентрации

Вопросы:
Показатели дифференциации:
Децильный коэффициент
Фондовый коэффициент
2. Показатели концентрации:
Коэффициент Герфиндаля
Коэффициент Джини
Коэффициент Лоренца

При необходимости более подробного изучения структуры вариационного ряда, рассчитываются показатели, аналогичные медиане.
Для этого вариационный ряд делится на большее число групп, равных по числу единиц в каждой группе.
Квартильные группы –
4 группы по 25% единиц в каждой группе
Квинтильные группы –
5 групп по 20 % единиц в каждой группе
Децильные группы –
10 групп по 10% единиц в каждой группе

Децили – это максимальные значения признака
в соответствующих децильных группах:
Д1 – первый дециль (значение признака у 10%-ой единицы)
Д2 – второй дециль (значение признака у 20%-ой единицы)
…
…
…
Д9 – девятый дециль (значение признака у 90%-ой единицы)
Д10 – десятый дециль (значение признака у 100%-ой единицы), максимальное значение признака в данном вариационном ряду.

Децильный коэффициент дифференциации (КД)

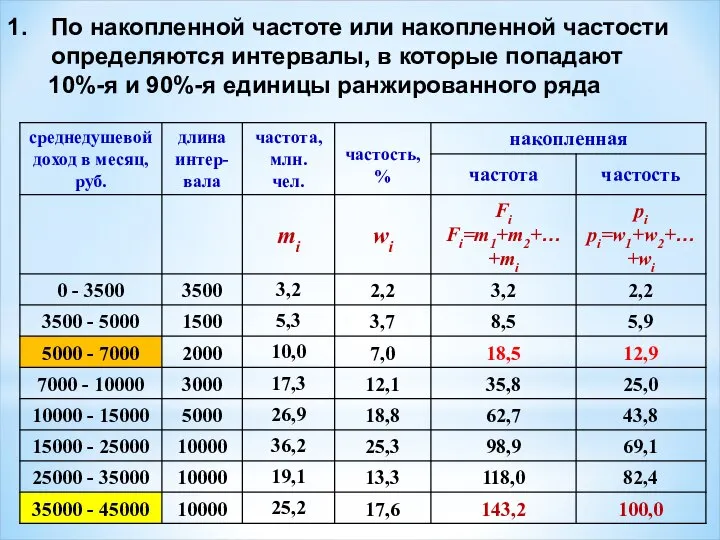
По накопленной частоте или накопленной частости определяются интервалы, в которые попадают 10%-я и 90%-я единицы ранжированного ряда

2. Рассчитывается Д9 – девятый дециль (значение признака
у 90%-й единицы)
где xk-1 – нижняя граница интервала, содержащего девятый дециль;
Δxk – длина интервала, содержащего девятый дециль;
Fk-1 (pk-1) – частота (частость), накопленная до интервала, содержащего девятый дециль;
mk (wk) – частота (частость) интервала, содержащего девятый дециль.

3. Рассчитывается Д1 – первый дециль (значение признака
у 10%-й единицы)
где xk-1 – нижняя граница интервала, содержащего первый дециль;
Δxk – длина интервала, содержащего первый дециль;
Fk-1 (pk-1) – частота (частость), накопленная до интервала, содержащего первый дециль;
mk (wk) – частота (частость) интервала, содержащего первый дециль.

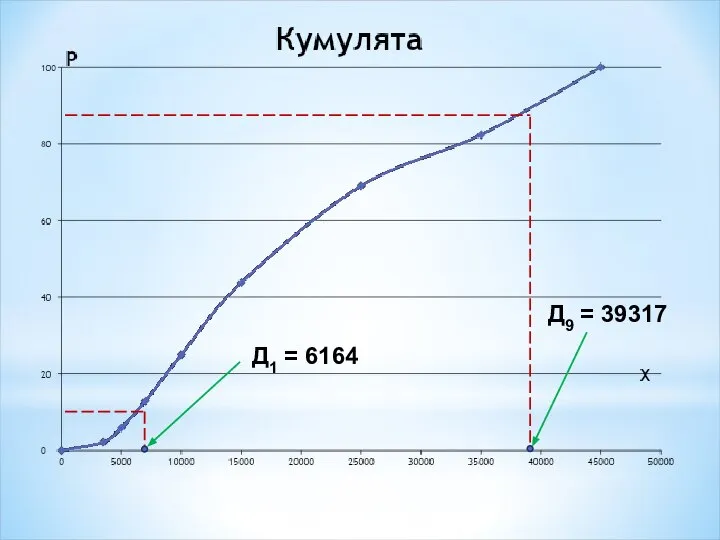
Д9 = 39317
Д1 = 6164

Показывает, во сколько раз
значение признака 90%-й единицы (девятый дециль - Д9) больше
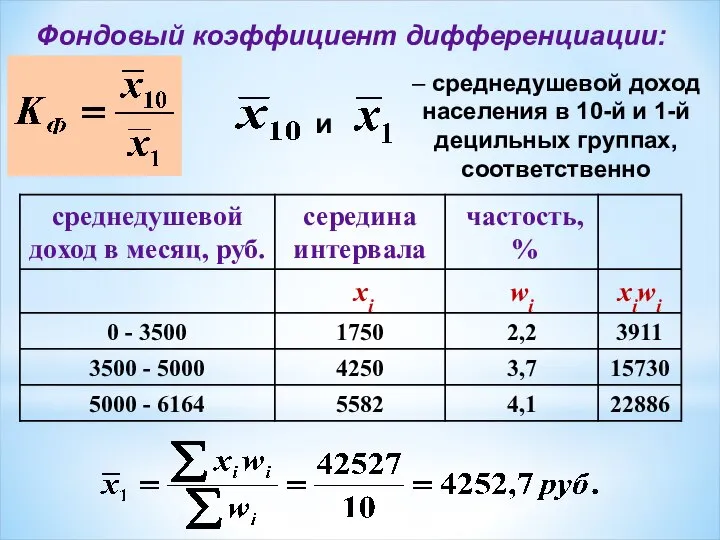
значения признака 10%-й единицы (первого дециля Д1)

и
– среднедушевой доход населения в 10-й и 1-й децильных группах, соответственно
Фондовый коэффициент дифференциации:

Фондовый коэффициент показывает во сколько раз среднее значение признака в десятой децильной группе больше среднего значения признака в первой децильной группе

ПОКАЗАТЕЛИ
КОНЦЕНТРАЦИИ

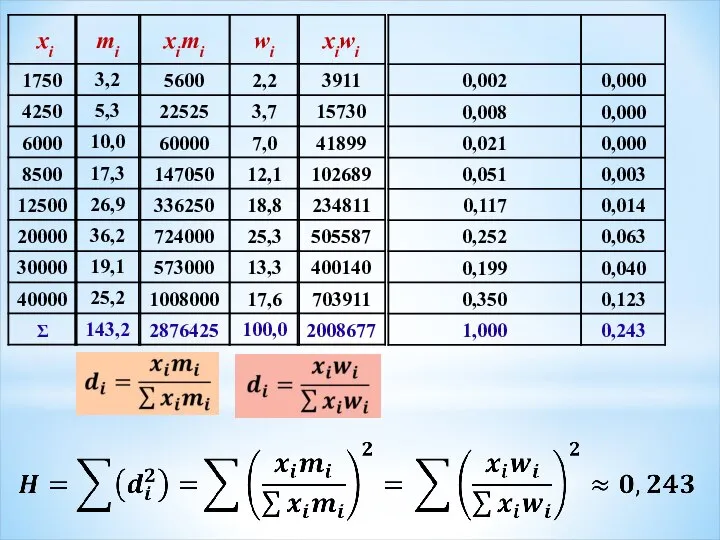
Коэффициент Герфиндаля:
Определяется как сумма квадратов долей изучаемого признака выделенных групп
в общей сумме признака

Рассмотрим случай крайне неравномерного распределения признака по группам:

Пределы изменения
коэффициента Герфиндаля
Отличие фактического значения коэффициента Герфиндаля (H) от возможного
в данном ряду минимального значения (Hmin)
указывает на наличие доминирующих групп в этом ряду.
Близость коэффициента Герфиндаля (H) к 1
характеризует неравномерность распределения изучаемого признака по выделенным группам.

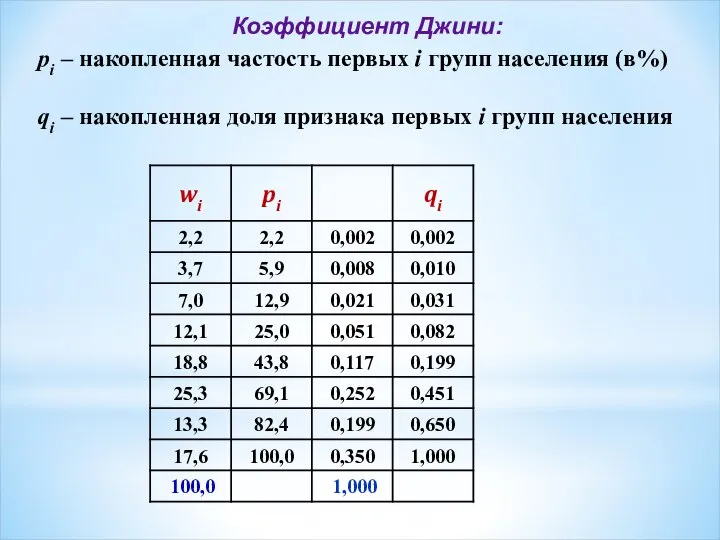
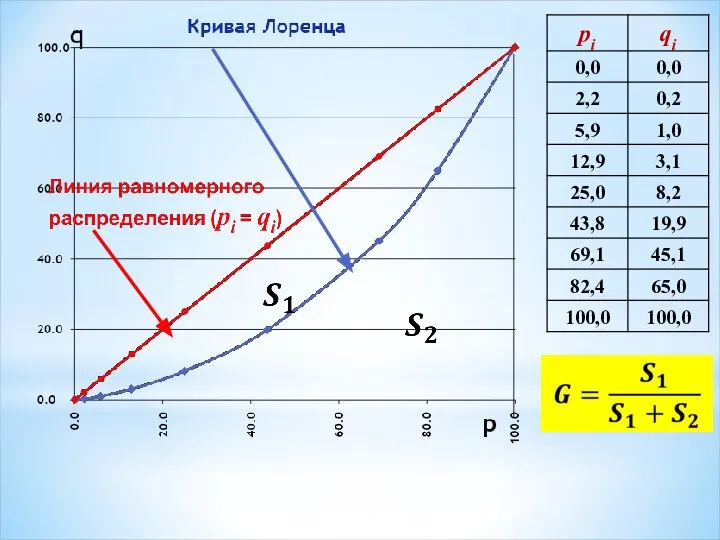
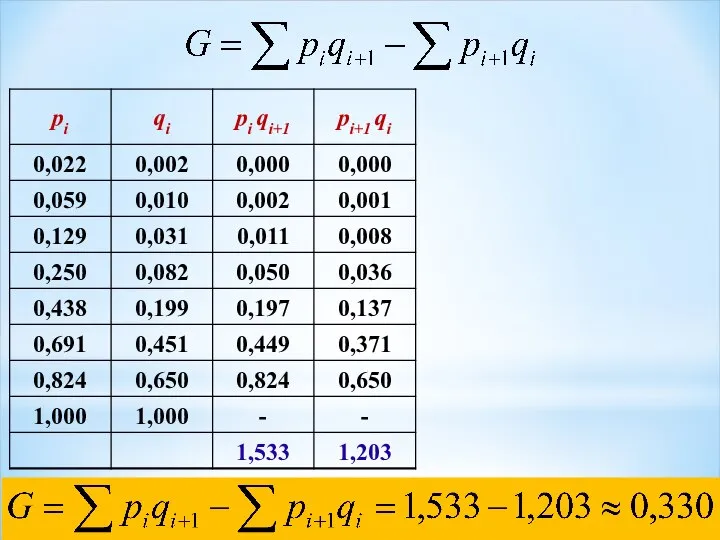
Коэффициент Джини:
pi – накопленная частость первых i групп населения (в%)
qi – накопленная доля признака первых i групп населения

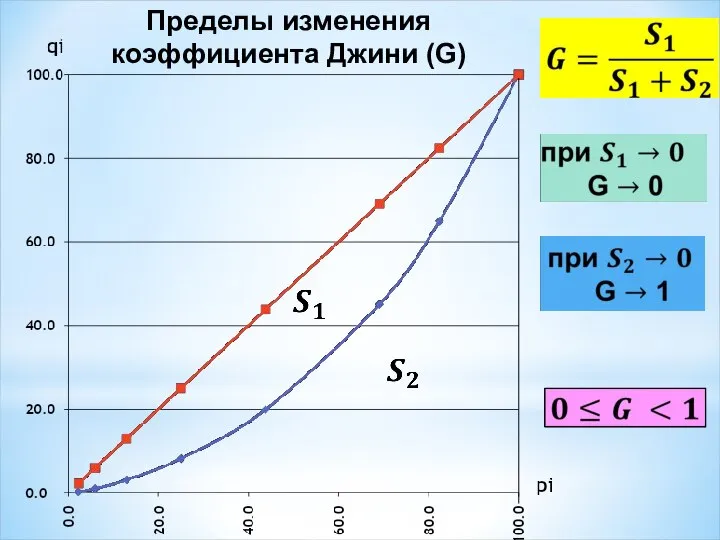
Пределы изменения
коэффициента Джини (G)

*Допускается расчет
коэффициента Джини в процентах

Величина коэффициента Джини (G) характеризует степень концентрации изучаемого признака у единиц наблюдения в выделенных группах.

Коэффициент Лоренца
Допускается расчет
коэффициента Лоренца в %