Признак перпендикулярности двух плоскостей

перпендикулярные плоскости
Сегодня на уроке:
признак перпендикулярности двух плоскостей

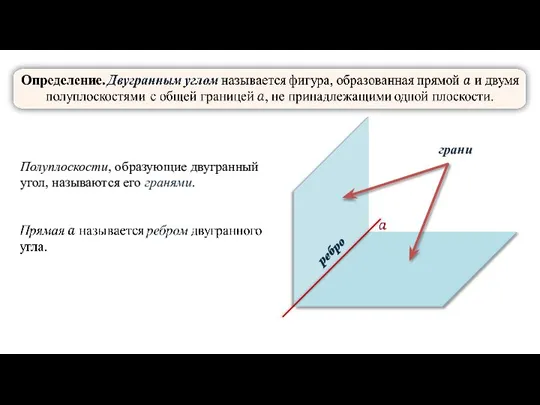
Полуплоскости, образующие двугранный угол, называются его гранями.
грани
ребро

Определение. Углом между пересекающимися плоскостями называется угол между прямыми, проведенными в плоскостях перпендикулярно их линии пересечения через некоторую точку.

Если в пространстве пересекаются две плоскости, то они образуют
четыре двугранных угла с общим ребром.
Если известен один из этих двугранных углов, то можно найти и другие три двугранных угла.

Взаимно перпендикулярные плоскости

Теорема (Признак перпендикулярности двух плоскостей).
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Доказательство.
Теорема доказана.

Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
Доказательство.
Что и требовалось доказать.

Следствие. Прямая, проведенная в одной из двух перпендикулярных плоскостей перпендикулярно прямой, по которой они пересекаются, перпендикулярна другой плоскости.
Доказательство.
Что и требовалось доказать.

Доказательство.
Что и требовалось доказать.