Содержание
- 2. БИНАРНЫЕ ОТНОШЕНИЯ в Z: 8>5 – истинно; 5>10 – ложно На множестве точек плоскости: Можно сказать,
- 3. БИНАРНЫЕ ОТНОШЕНИЯ На множестве X определено бинарное отношение, если задано подмножество R декартова произведения X×X Бинарное
- 4. Способы задания бинарного отношения 1. Перечисление элементов: R={(1,1),(2,2),(6,6),(1,2),(1,6),(2,6)} определено на множестве X={1,2,6} 2. Бинарное отношение -
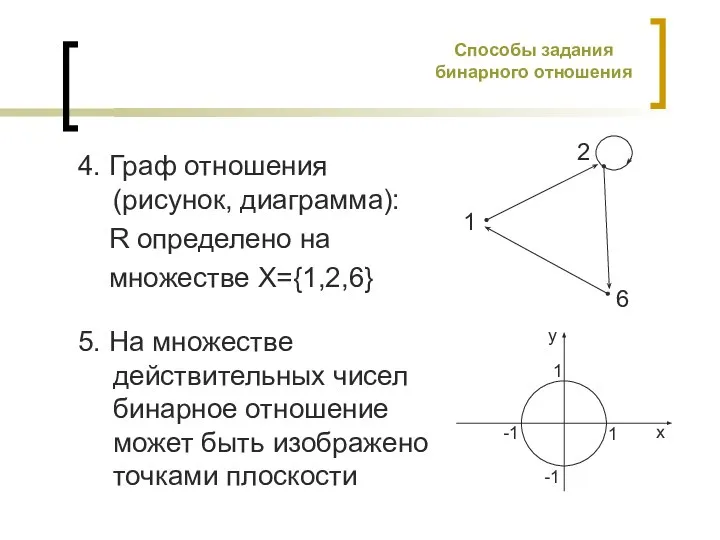
- 5. Способы задания бинарного отношения 4. Граф отношения (рисунок, диаграмма): R определено на множестве X={1,2,6} 5. На
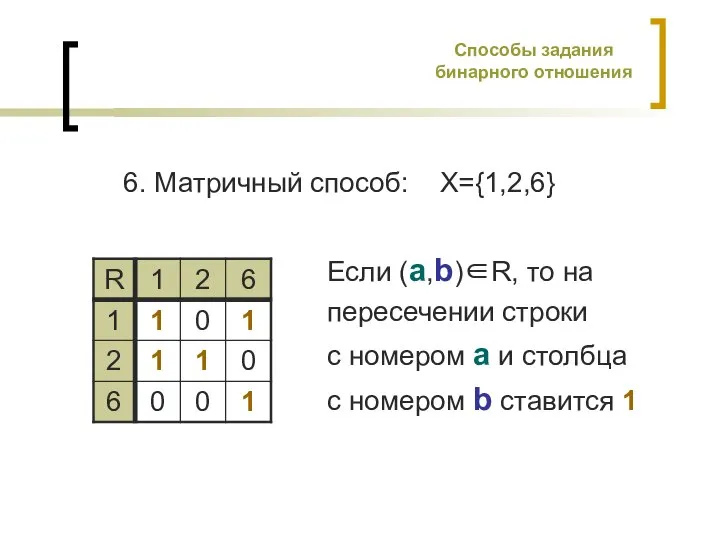
- 6. 6. Матричный способ: X={1,2,6} Если (a,b)∈R, то на пересечении строки с номером a и столбца с
- 7. Свойства бинарного отношения R - бинарное отношение, определенное на множестве X 1. R рефлексивно, если ∀x∈X
- 8. Свойства бинарного отношения R - бинарное отношение, определенное на множестве X 3. R транзитивно, если ∀x,y,z∈X
- 9. R - бинарное отношение, определенное на множестве X 6. R линейно, если ∀x,y∈X [ (x,y)∈R V
- 10. Отношение порядка Отношение частичного порядка – рефлексивное, транзитивное и антисимметричное бинарное отношение R1 = { (x,y)∈Z×Z
- 11. Частично упорядоченное множество A≠∅ – ЧУМ Частично упорядоченное множество – множество, на котором задано отношение частичного
- 12. Частично упорядоченное множество Элемент a∈A частично упорядоченного множества называется наибольшим элементом, если ∀x∈A x ≤ a
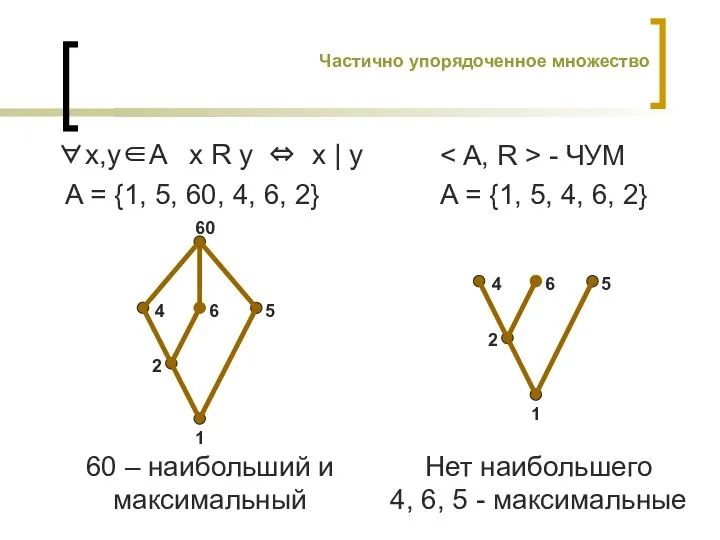
- 13. A = {1, 5, 60, 4, 6, 2} ∀x,y∈A x R y ⇔ x | y
- 14. Отношение эквивалентности Отношение эквивалентности – рефлексивное, симметричное и транзитивное бинарное отношение R1 = { (x,y)∈Z×Z |
- 15. УПРАЖНЕНИЕ Докажите: ∀m∈Z m>1 R = { (x,y)∈Z×Z | (x-y) кратно m } – отношение эквивалентности
- 16. Классы эквивалентности Семейство { Xk | k∈K, Xk⊆X } образует разбиение множества X на классы Xk,
- 17. Классы эквивалентности Всякому разбиению множества X на классы Xk отвечает бинарное отношение R, задаваемое следующим образом:
- 18. Пусть ~ – отношение эквивалентности, заданное на X, и a∈X Класс Ka эквивалентности ~ c порождающим
- 19. Свойства классов эквивалентности Пусть ~ – отношение эквивалентности, заданное на X 1) Любой класс Ka не
- 20. Свойства классов эквивалентности Пусть ~ – отношение эквивалентности, заданное на X 4) Элементы из разных классов
- 21. ТЕОРЕМА Всякое отношение эквивалентности, заданное на множестве X, определяет разбиение множества X на классы эквивалентности Доказательство:
- 22. Доказательство ТЕОРЕМЫ Следовательно, { Xk | k∈K, Xk⊆X } образует разбиение множества X на классы Xk
- 23. Фактор-множество Фактор-множеством множества X по отношению эквивалентности R называется множество, каждый элемент которого является одним из
- 25. Скачать презентацию



















 Геометрический конструктор: Развивающая игра Танграм
Геометрический конструктор: Развивающая игра Танграм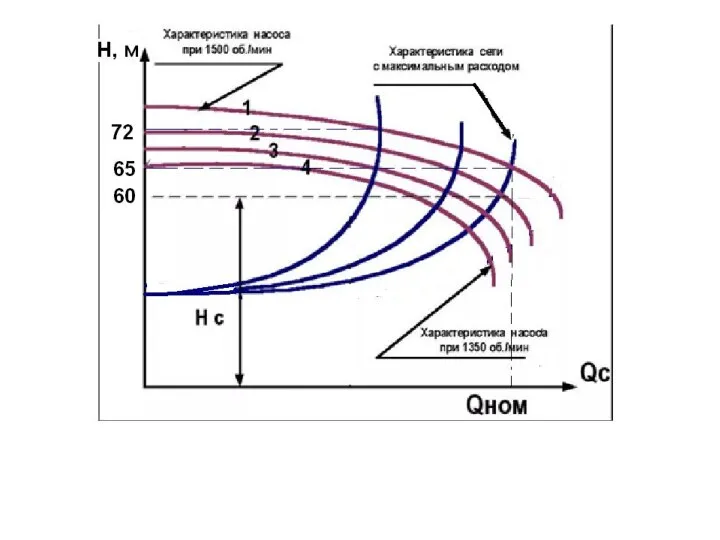 Модель частотно-регулируемого привода. (Тема 8)
Модель частотно-регулируемого привода. (Тема 8) Веселый счет. Викторина
Веселый счет. Викторина Производная сложной функции
Производная сложной функции Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Обобщение и систематизация знаний и умений по теме Взаимное расположение прямых в пространстве. Параллельные прямые
Обобщение и систематизация знаний и умений по теме Взаимное расположение прямых в пространстве. Параллельные прямые Мир в поверхности цилиндра
Мир в поверхности цилиндра Сложение чисел с разными знаками
Сложение чисел с разными знаками Многоугольники. Их формы
Многоугольники. Их формы Синус, косинус, тангенс и котангенс
Синус, косинус, тангенс и котангенс Развёртка куба
Развёртка куба Математика в танце
Математика в танце Линейное уравнение с одной переменной (7 класс)
Линейное уравнение с одной переменной (7 класс) Прямоугольник. Квадрат. Периметр многоугольника
Прямоугольник. Квадрат. Периметр многоугольника Естественный отбор. Бинарный урок по биологии и математике (часть 3)
Естественный отбор. Бинарный урок по биологии и математике (часть 3) Понятие обыкновенной дроби. Упражнения
Понятие обыкновенной дроби. Упражнения Урок математики. 1 класс
Урок математики. 1 класс Ответы для самопроверки
Ответы для самопроверки Квадратный корень и его свойства
Квадратный корень и его свойства Математика в кинематографии
Математика в кинематографии Решение задач на готовых чертежах. Геометрия. 9 класс
Решение задач на готовых чертежах. Геометрия. 9 класс Презентация на тему Окружность и круг (5 класс)
Презентация на тему Окружность и круг (5 класс)  Работа над ошибками
Работа над ошибками Алгоритм вычисления площади с помощью палетки
Алгоритм вычисления площади с помощью палетки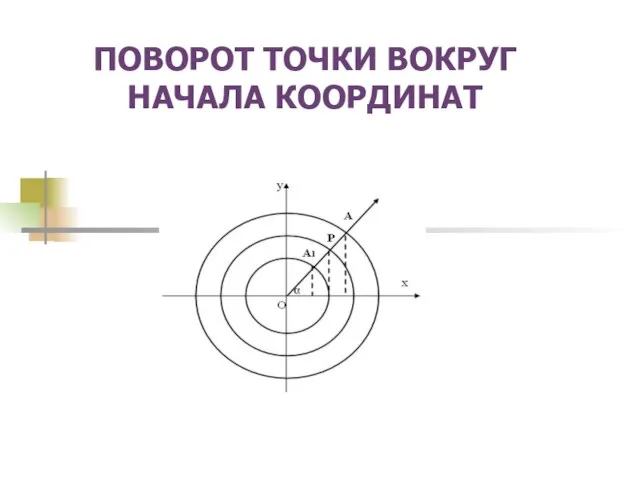 ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Презентация на тему Параллелепипед (9 класс)
Презентация на тему Параллелепипед (9 класс)  Алгоритм фронта волны
Алгоритм фронта волны Числовая последовательность. Арифметическая прогрессия и геометрическая прогрессия
Числовая последовательность. Арифметическая прогрессия и геометрическая прогрессия