Буквенная запись свойств действий над числами

16.11.20
алгебра

Цели урока:
повторить свойства действий над числами;
научиться записывать их с использованием букв;
совершенствовать вычислительные навыки;
применять свойства действий над числами для нахождения площадей фигур.

«Алгебра есть не что иное, как математический язык, приспособленный для обозначения отношений между величинами.»
Исаак Ньютон
(1606—1642)
английский физик, математик,
механик и астроном

120 + 157 =
157 + 120 =
0,27 + 1,52 =
1,52 + 0,27 =
277
277
1,79
1,79
9
9
1. Переместительное свойство сложения:
для любых a и b
a + b = b + a
От перестановки слагаемых сумма не меняется.

-20
-20
31
31
2. Переместительное свойство умножения:
для любых a и b
a * b = b * a
От перестановки множителей произведение не меняется.

Вычислите удобным для вас способом
(115 + 3,71) + 1,29 =
115 + (3,71 + 1,29)= 120
для любых a, b и c
(a + b) + с = a + (b + c) = a + b +c
3. Сочетательное свойство сложения:
Чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.

4. Сочетательное свойство умножения:
для любых a, b и c
(a * b)*c = a*(b*c) = abc
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

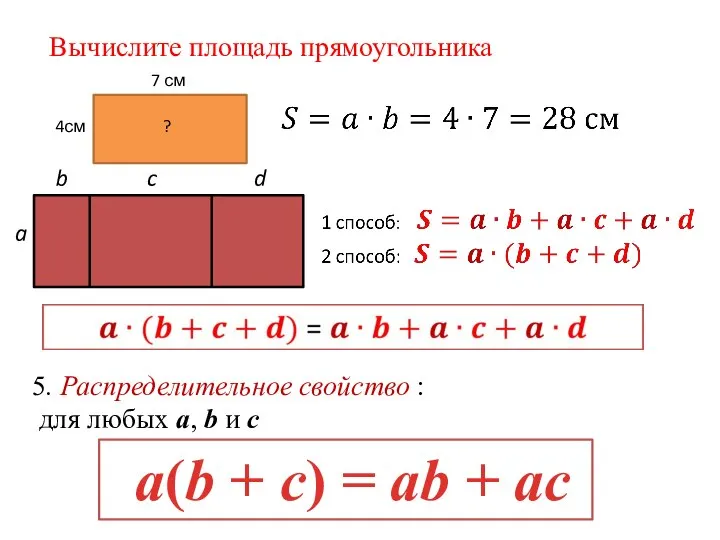
Вычислите площадь прямоугольника
5. Распределительное свойство :
для любых a, b и c a(b + c) = ab + ac

256 + (100 – 2) = (256 + 100) – 2 = 356 – 2 = 354.
a + (b – c) = (a + b) – c.
б) 138 + (100 +6) = (138 + 100) + 6 = 238 + 6 = 244.
a + (b +c) = (a + b) +c.
в) 87 – (50 – 1) = (87 – 50) +1 = 37 +1 = 38.
a – (b – c) = (a – b) + c.
г) (100 – 6) – 61 = (100 – 61) – 6 = 39 – 6 = 33.
(a – b) – c = (a –c) – b.

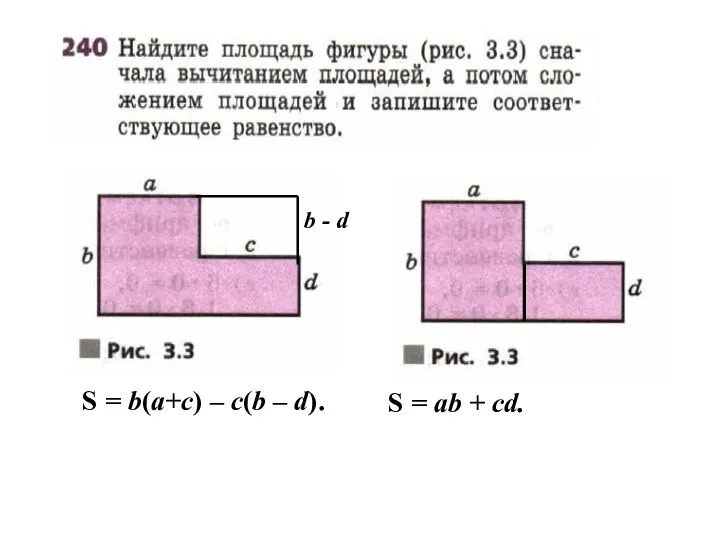
b - d
S = b(a+c) – c(b – d).
S = ab + cd.

Домашнее задание
1. Прочитайте с.73-75 учебника.
2.Назовите и запишите в буквенном виде в тетрадь основные свойства сложения и умножения чисел (1-5)
3. Какие вычислительные приемы рассмотрены в примерах 1 и 2(стр. 74) ?
Назовите и запишите соответствующие равенства с помощью букв.
4.Выполните номера 240(из презентации) и 241 в тетради.