Содержание
- 2. Матрицы
- 3. Матрицей размерности m x n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. где
- 4. Матрица, все элементы которой равны нулю, называется нулевой и обозначается через О.
- 5. Единичная матрица Е – это диагональная матрица, в которой все элементы главной диагонали равны единице, т.е.
- 6. Пример
- 7. Пример
- 8. Пример Вычислить 4А - 3B, если Решение: 4А - 3B = 4А + (-3)B
- 9. 4. Умножение матриц Опр. 17. Произведение матрицы А на матрицу В, определено тогда и только тогда,
- 10. Найти произведение матриц АB и BA Решение: Произведение матриц АB существует, т.к. матрица А имеет размерность
- 11. ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ
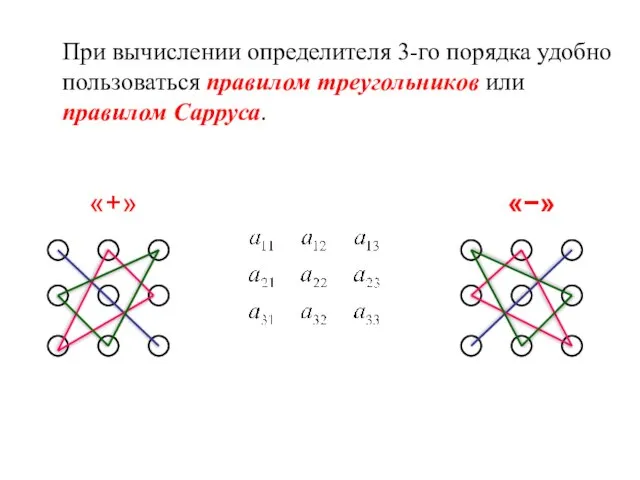
- 12. При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников или правилом Сарруса. «+» «−»
- 13. Пример Вычислить определители матриц:
- 14. Опр.2. Минором элемента aij матрицы n-го порядка A называется определитель матрицы (n-1)-го порядка, полученный из матрицы
- 15. Пример. Найти миноры M11, M32, M43
- 16. Опр.4. Алгебраическим дополнением элемента аij матрицы n-го порядка А называется число, равное (-1)i+jMij и обозначаемое символом
- 17. Определитель n-го порядка матрицы Аn равен сумме произведений элементов любой строки (или столбца) на их соответствующие
- 18. Пример По 2-ой строке:
- 19. Пример По 3-му столбцу:
- 20. Определитель n-го порядка треугольной матрицы равен произведению элементов главной диагонали. Определитель n-го порядка единичной матрицы E
- 21. Ранг матрицы
- 22. Элементарными преобразования матрицы называются : Транспонирование (замена строк столбцами) Перестановка строк и столбцов. Умножение некоторой строки
- 23. Теорема о ранге матрицы
- 24. ОБРАТНАЯ МАТРИЦА
- 25. Опр. 1. Матрица А-1 называется обратной для квадратной матрицы А, если АА-1 = А-1А = Е
- 26. Всякая невырожденная матрица Аn имеет обратную матрицу А-1, причем где Аij – алгебраические дополнения элементов aij
- 27. Пример Найти матрицу, обратную к данной: Решение: Т.к. |А|=-2≠0, то матрица А – невырожденная и имеет
- 28. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 29. Опр. Системой m линейных уравнений с n неизвестными (СЛУ) называется система уравнений где x1, x2, …
- 30. Опр. Матрица А составленная из коэффициентов СЛУ называется основной матрицей системы.
- 31. Опр. Матрицы X и B называются матрицы-столбцы неизвестных и свободных членов.
- 32. Матричная форма записи СЛУ:
- 33. Пример. Записать в матричной форме
- 34. Решение Обозначим Следовательно, имеем AX = B.
- 35. Рассмотрим частный случай неоднородной системы, когда m=n, т.е. систему вида Определитель |А| основной матрицы системы В
- 36. Пример. Решить систему
- 37. Решение. т.е. исходная система трех неоднородных линейных уравнений с тремя неизвестными имеет единственное решение. Найдем единственное
- 39. Следовательно, обратная матрица равна
- 40. Найдем теперь решение системы
- 41. Проверка
- 42. Правило Крамера Согласно правилу Крамера, если |A| ≠ 0, то единственное решение СЛУ вычисляется по следующим
- 43. Найдем теперь решение системы по правилу Крамера
- 44. МЕТОД ГАУССА
- 45. Элементарными называются следующие преобразования системы: Перестановка местами двух уравнений системы. Умножение некоторого уравнения системы на число,
- 47. Скачать презентацию



































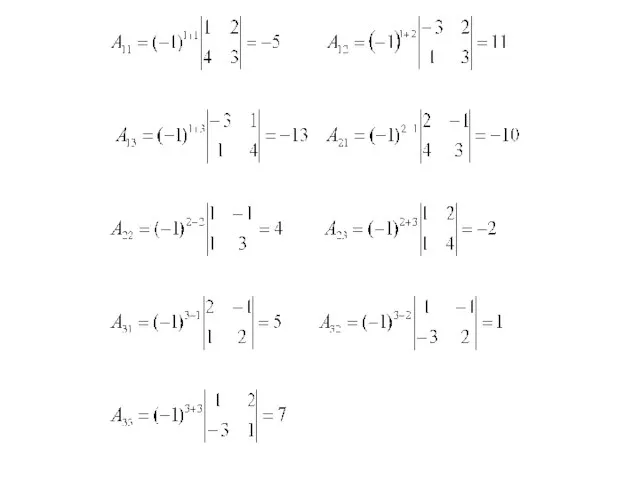







 Примеры арифметических операций
Примеры арифметических операций Презентация по математике "Праздник чисел «5 плюс »" -
Презентация по математике "Праздник чисел «5 плюс »" -  Презентация на тему Построение сечений тетраэдра
Презентация на тему Построение сечений тетраэдра  Арифметическая прогрессия
Арифметическая прогрессия Золотое сечение
Золотое сечение Игра Жизнь Conway's Game of Life
Игра Жизнь Conway's Game of Life Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Круглые тела
Круглые тела Функція реакції
Функція реакції Построение треугольника
Построение треугольника Двугранный угол
Двугранный угол Тройные и многократные интегралы
Тройные и многократные интегралы Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Значение логического выражения (тема № 3)
Значение логического выражения (тема № 3) Таблица умножения трёх
Таблица умножения трёх Приближенные вычисления
Приближенные вычисления Производная сложной функции
Производная сложной функции 20b
20b Параллелепипед. Виды параллелепипедов
Параллелепипед. Виды параллелепипедов Разделительное свойство умножения
Разделительное свойство умножения Дискриминантный анализ
Дискриминантный анализ Пропорции. Проценты
Пропорции. Проценты Компьютерный и интеллектуальный анализ данных. Теория вероятностей
Компьютерный и интеллектуальный анализ данных. Теория вероятностей Интерактивный тренажёр Весёлый счёт. Математика 1 класс
Интерактивный тренажёр Весёлый счёт. Математика 1 класс Тела вращения
Тела вращения Логика. Задания
Логика. Задания Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира параллельность прямых и плоскостей 10
параллельность прямых и плоскостей 10