Содержание
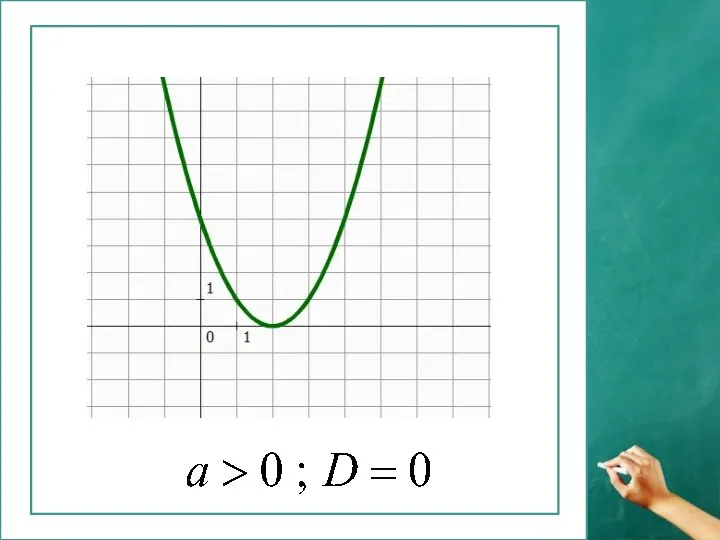
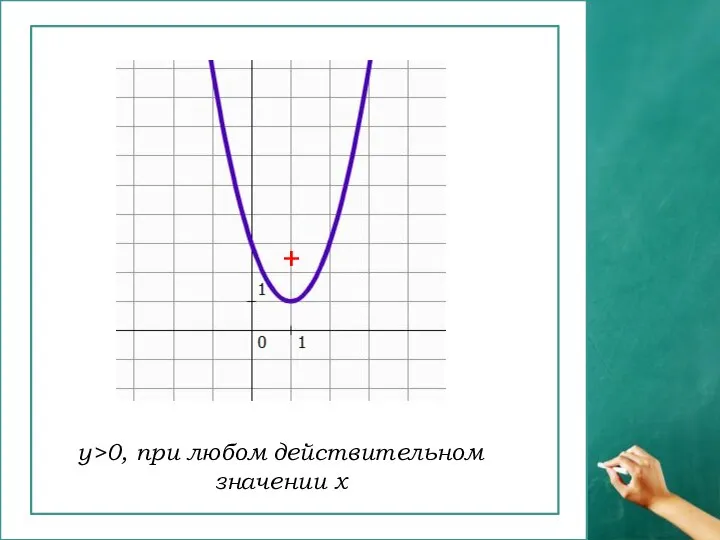
- 9. у>0, при любом действительном значении х +
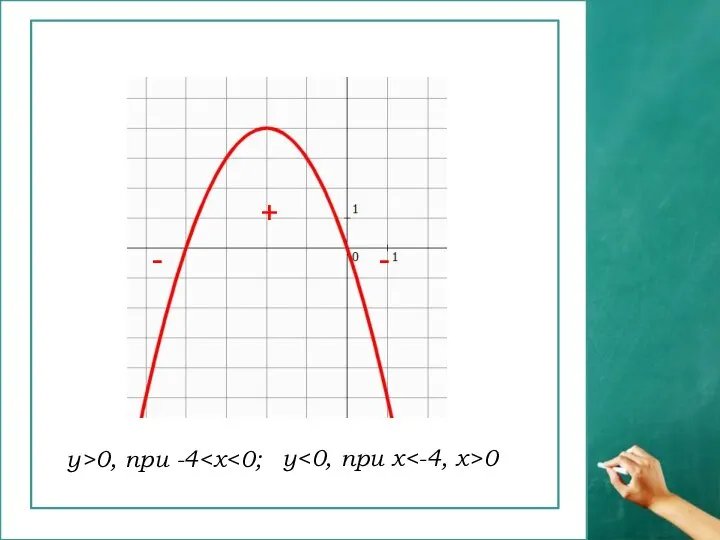
- 10. у>0, при -4 y 0 + - -
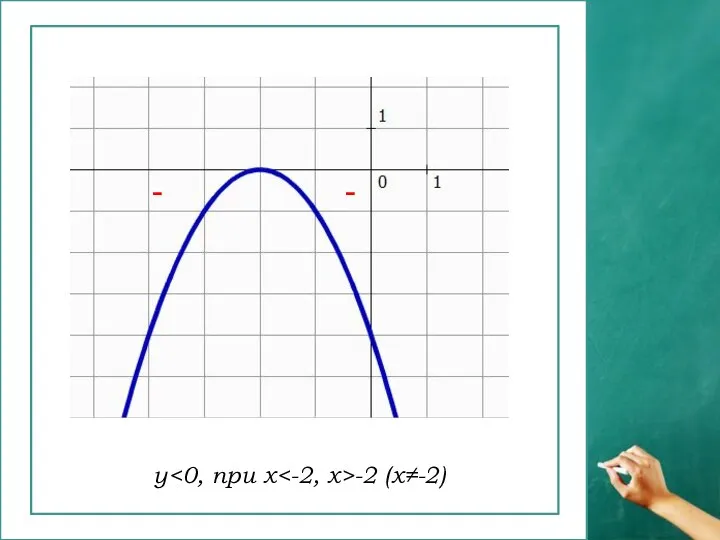
- 11. y -2 (х≠-2) - -
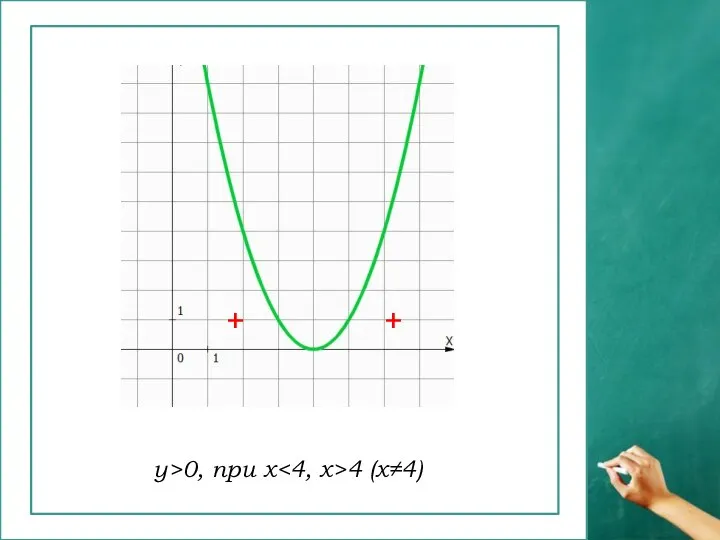
- 12. у>0, при x 4 (х≠4) + +
- 14. Решение квадратного неравенства с помощью графика квадратичной функции 18 марта 2014 год Цель: научиться решать квадратные
- 15. Алгоритм решения квадратного неравенства с помощью графика квадратичной функции: 1. Приведите неравенство к виду 2. Рассмотрите
- 16. h - высота подъема тела над землей, h0 - начальная высота тела над землей, V0 -
- 17. Задача: Мотоциклист совершает прыжок через 10 установленных в ряд автобусов. Длина ряда 40 м. До какой
- 18. Задача из открытого банка ЕГЭ: Модель камнеметательной машины, выстреливает камни под определенным углом к горизонту с
- 20. Скачать презентацию

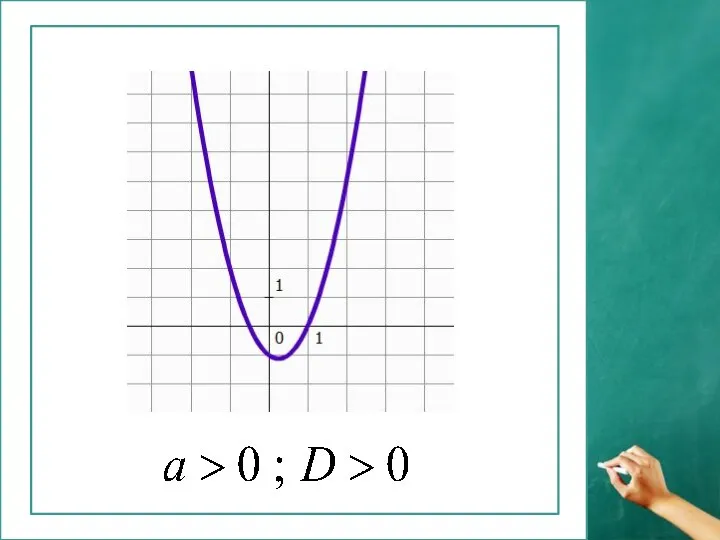
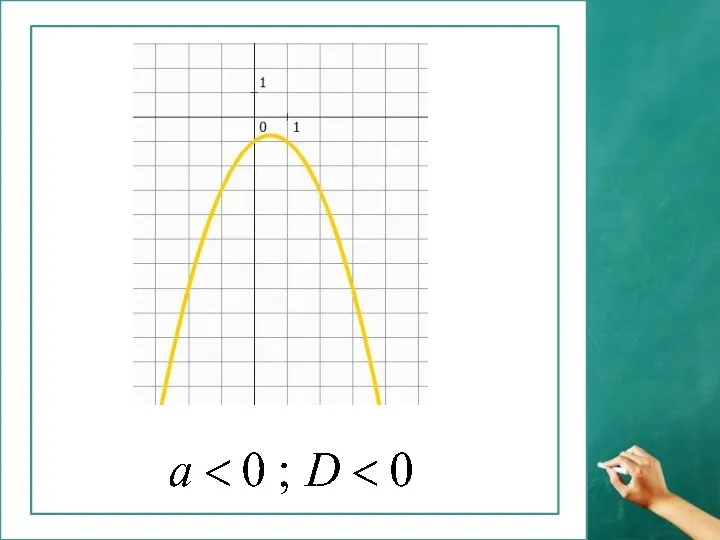
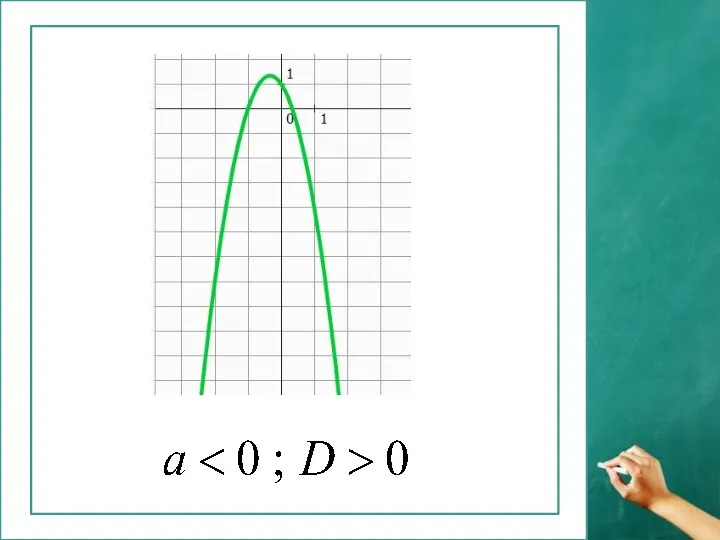

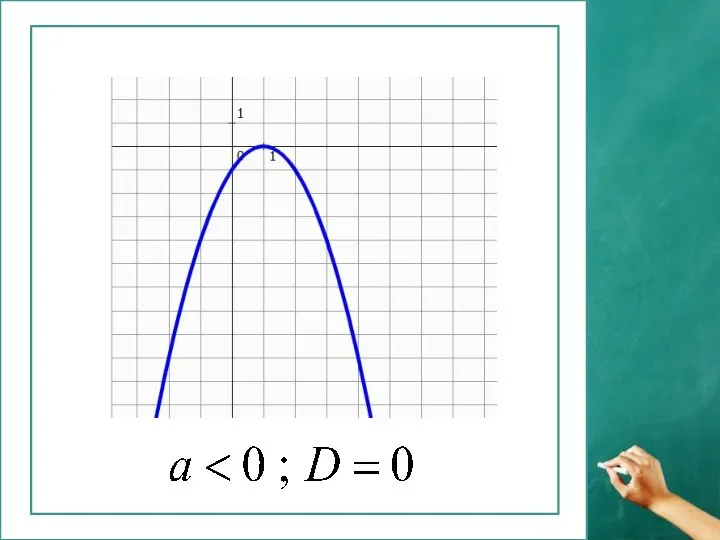
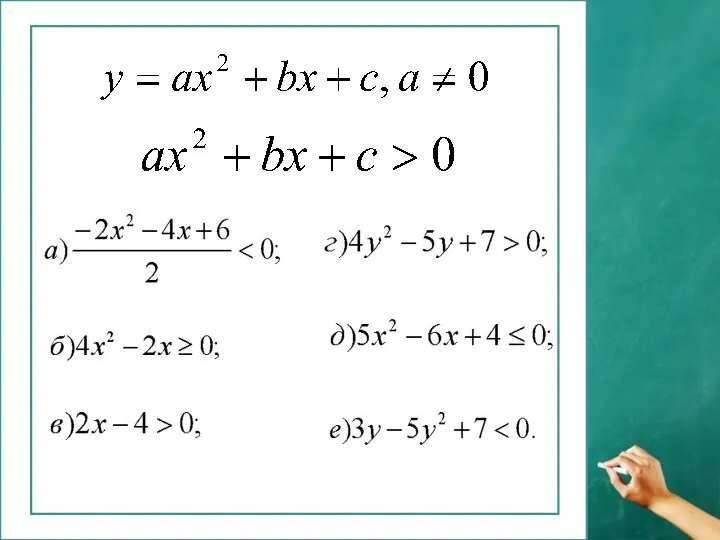





 Презентация на тему Прямоугольная система координат
Презентация на тему Прямоугольная система координат  Логические элементы
Логические элементы Страничка для любознательных
Страничка для любознательных Единица измерения объёма жидкости-литр
Единица измерения объёма жидкости-литр Религия Байеса
Религия Байеса Вычисление статистических характеристик случайных величин
Вычисление статистических характеристик случайных величин Геометрические приложения двойных интегралов
Геометрические приложения двойных интегралов Решение иррациональных уравнений
Решение иррациональных уравнений Возведение степени в степень
Возведение степени в степень Задачи с величинами цена, количество, стоимость
Задачи с величинами цена, количество, стоимость Подготовка к ЕГЭ. Разбор типовых заданий В9 (производная,интеграл)
Подготовка к ЕГЭ. Разбор типовых заданий В9 (производная,интеграл) Векторная алгебра
Векторная алгебра Обыкновенные дроб
Обыкновенные дроб Свойство параллельности
Свойство параллельности Свойства логарифмов положительного числа
Свойства логарифмов положительного числа Задачи по геометрии
Задачи по геометрии Парная регрессия: линейный анализ
Парная регрессия: линейный анализ Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспортир
Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспортир Многогранники в нашей жизни
Многогранники в нашей жизни Решение задач на применение признаков подобия
Решение задач на применение признаков подобия Решение систем уравнений графическим и аналитическим способом
Решение систем уравнений графическим и аналитическим способом Многогранники. Тетраэдр
Многогранники. Тетраэдр Функция. Предел функции. (часть 1)
Функция. Предел функции. (часть 1) Теорема Пифагора
Теорема Пифагора Великие математики
Великие математики Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Окружность и круг. Задачи
Окружность и круг. Задачи