Содержание
- 2. Цели: 1. Расширить и углубить знания о прогрессиях; 2. Организация деятельности учащихся по изучению нахождения суммы
- 3. а) Какая числовая последовательность называется геометрической прогрессией? б) Что называется знаменателем геометрической прогрессии? в) Как задается
- 4. Среди последовательностей распознать арифметическую прогрессию и геометрическую прогрессию, а также вставить пропущенное число:
- 5. Договор. Я обязуюсь ежедневно в течении 30 дней приносить вам по 100000 рублей. А вы обязуетесь
- 6. -Ребята, кто может сформулировать тему нашего сегодняшнего урока?
- 7. Тема: «Геометрическая прогрессия. Сумма n- первых членов геометрической прогрессии».
- 8. Дано: (bn) – геометрическая прогрессия b1= 1, q=2 Найти S30 Решение: S30=1+2+4+8+16+…=1073741823 коп = 10737418,23 руб.
- 9. Неудобно и громоздко! Проблема: нельзя ли решить эту задачу проще? Можно. Но для этого нужно познакомиться
- 10. МЫ С ТОБОЮ ТАК ПОХОЖИ
- 24. На первую клетку шахматной доски положить одно зерно, на вторую – в два раза больше, т.е.
- 25. Дано: (bn) – геометрическая прогрессия b1=1, q = 2, n = 64. Найти: S64 Решение 1)
- 26. Индусский царь не в состоянии был выдать Сете обещанную награду. Если бы царю удалось засеять пшеницей
- 27. Формула суммы n первых членов геометрической прогрессии, в которой q ≠ 0
- 28. Решим задачи (вместе) а) Дано: (bn)- геометрическая прогрессия. b1=8, q=1/2. Найти: S5. б) Дано: (bn)- геометрическая
- 29. Самостоятельная работа 1. Найти сумму 5 первых членов геометрической прогрессии, в которой b1=4, q=2. 2. Найти
- 30. Рефлексия 1. Я запомнил, что… 2. Что было легко? 3. Что было трудно? 4. Оцените свою
- 32. Скачать презентацию




























 Параллельные прямые
Параллельные прямые Диаграммы и графики. 6 класс
Диаграммы и графики. 6 класс Математика в нашей жизни
Математика в нашей жизни Скалярное произведение векторов. Задачи
Скалярное произведение векторов. Задачи Понятие цилиндра и конуса
Понятие цилиндра и конуса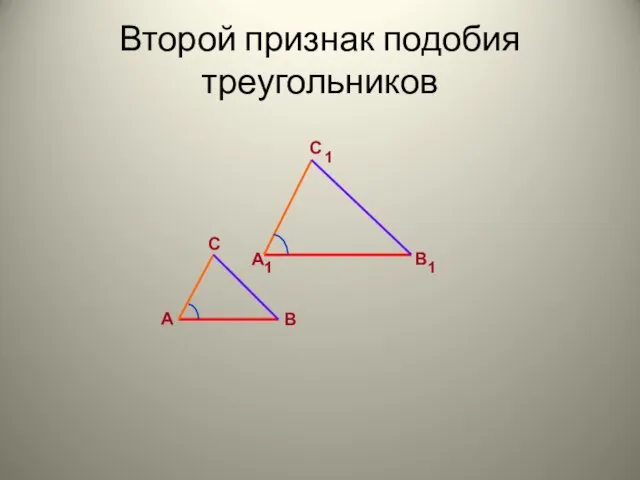 Второй признак подобия треугольников
Второй признак подобия треугольников Несократимые дроби
Несократимые дроби Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Основы математической статистики
Основы математической статистики Различные виды тестирования при изучении темы Десятичные дроби
Различные виды тестирования при изучении темы Десятичные дроби Математика в лицах
Математика в лицах Раскрытие скобок
Раскрытие скобок Когда выполнение одного условия обеспечивает выполнение другого
Когда выполнение одного условия обеспечивает выполнение другого Устная полянка
Устная полянка Логарифмическая линия в ЕГЭ
Логарифмическая линия в ЕГЭ Справочный материал. 9 класс
Справочный материал. 9 класс Математика. Задания на лето. Часть 4
Математика. Задания на лето. Часть 4 Определенный и неопред интеграл. Тема 8
Определенный и неопред интеграл. Тема 8 Методы многокритериальной оптимизации
Методы многокритериальной оптимизации Михаил Васильевич Ломоносов. Умножение и деление степеней с натуральными показателями
Михаил Васильевич Ломоносов. Умножение и деление степеней с натуральными показателями Проверочная работа. 5 класс
Проверочная работа. 5 класс Нахождение числа по его части. (6 класс. Тест №15)
Нахождение числа по его части. (6 класс. Тест №15) Степени с рациональными показателями, их свойства
Степени с рациональными показателями, их свойства Модель плоскости
Модель плоскости Математический турнир Умники и умницы
Математический турнир Умники и умницы Геометрический и физический смысл производной, вычисление производной. 11 класс
Геометрический и физический смысл производной, вычисление производной. 11 класс Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ  Powtórzenie do klasówki
Powtórzenie do klasówki