Булева алгебра

Перейдем к обозначениям, принятым в булевой записи

Дж. Буль –основатель логики
Операция, заданная на некотором множестве, называется бинарной, если она действует на два элемента этого множества и её результатом является элемент этого же множества.
Операция, заданная на некотором множестве, называется унитарной, если она действует на один элемент множества и её результатом является элемент этого же множества.
Булева алгебра есть множество В, содержащее специальные элементы 1 и 0, на котором заданы бинарные операции +

Для всех x, y, z из В должны выполняться аксиомы

1 – единичный элемент (единица),
0 – нулевой элемент (ноль),
– дополнение х.

Теорема. Для всех элементов х и у булевой алгебры выполняются соотношения:

Доказательство:

Доказательство:

Теорема. (Закон единственности дополнения) Дополнение произвольного элемента х булевой алгебры единственным образом определяется его свойствами:
Доказательство:

Доказательство:

Теорема. Для всех элементов х и у булевой алгебры имеют место соотношения:

Доказательство (а):
х – дополнение х’ . В соответствии с законом единственности дополнения

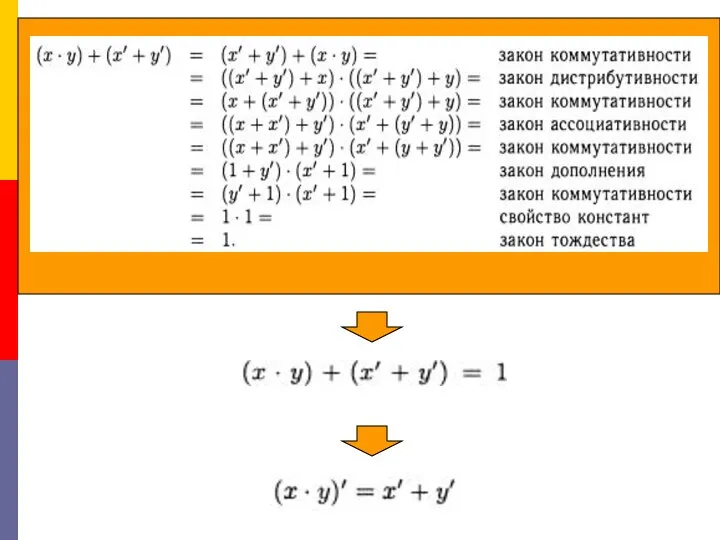
Каждая теорема обладает двойственностью.
Замена
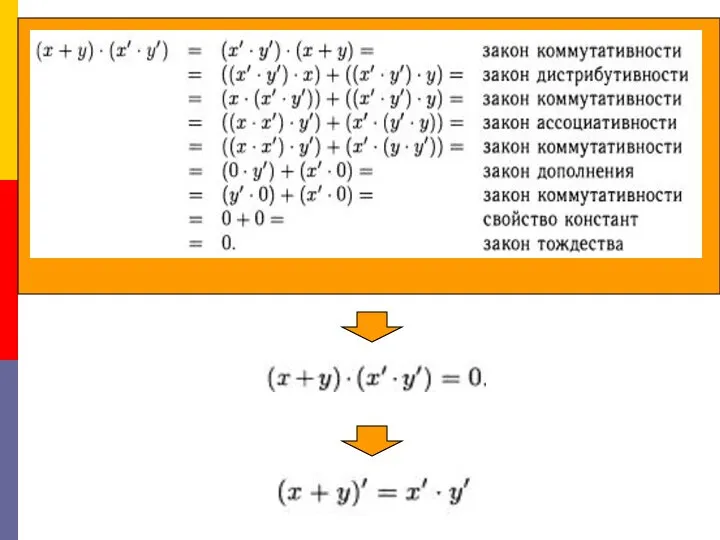
Первый закон де Моргана

Второй закон де Моргана

Подмножества произвольного множества А образуют булеву алгебру

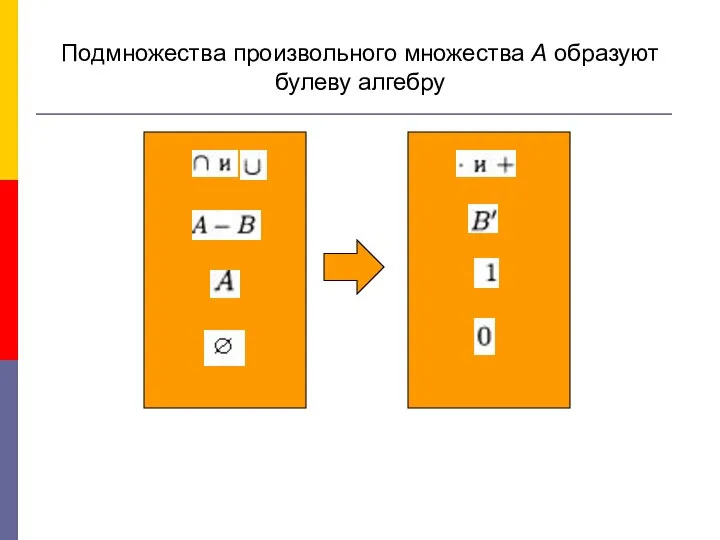
Теорема. Нулевой элемент 0 и единичный элемент 1 определены своими свойствами единственным образом.
Определение. Множество называется коконечным, если его дополнение конечно.
Теорема. Пусть универсальное множество U есть множество всех конечных и всех коконечных подмножеств множества положительных целых чисел. Подмножество U вместе с операциями объединения, пересечения и дополнения образуют булеву алгебру.