Содержание
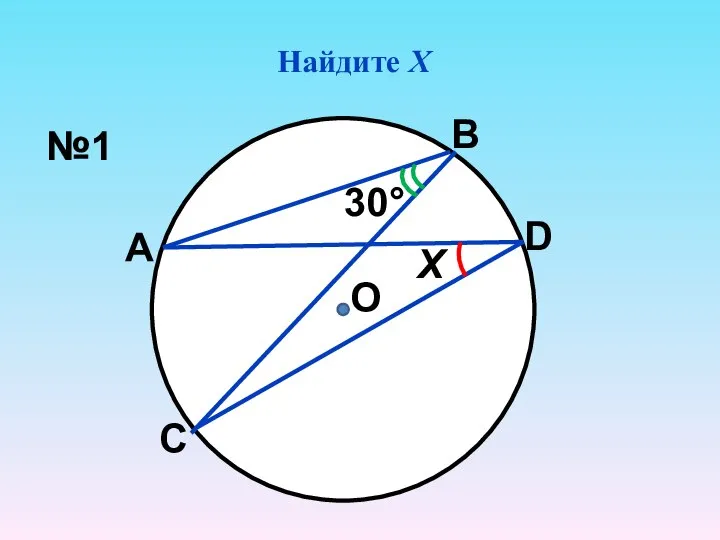
- 2. Найдите Х О 30° Х №1 А В С D
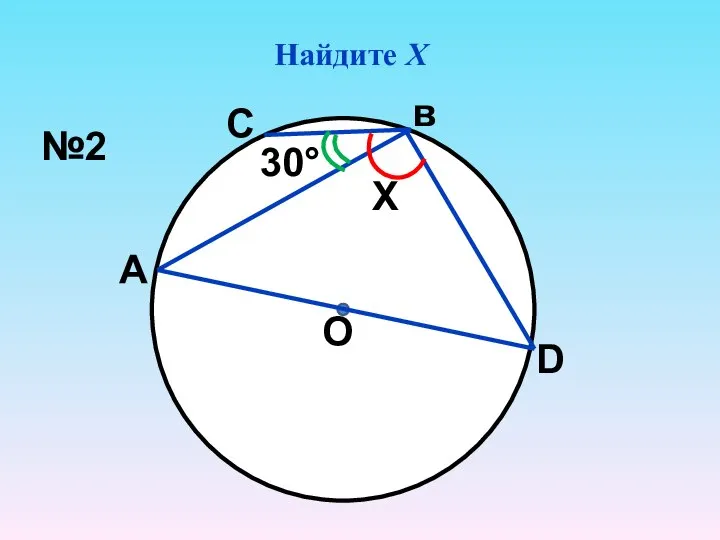
- 3. Найдите Х О 30° Х А С в D №2
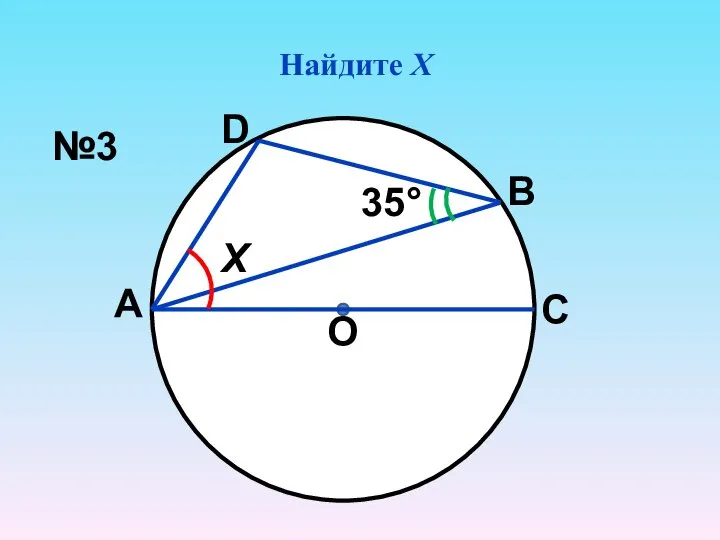
- 4. Найдите Х О 35° Х А С В D №3
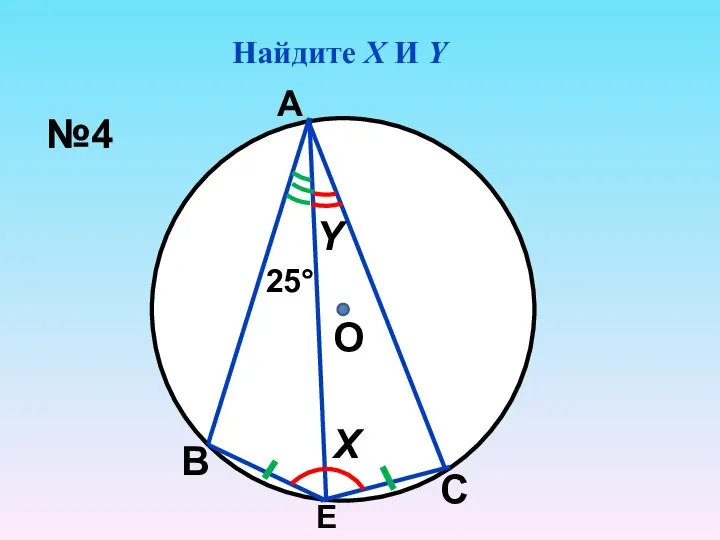
- 5. Найдите Х И Y О Х Y 25° А В С Е №4
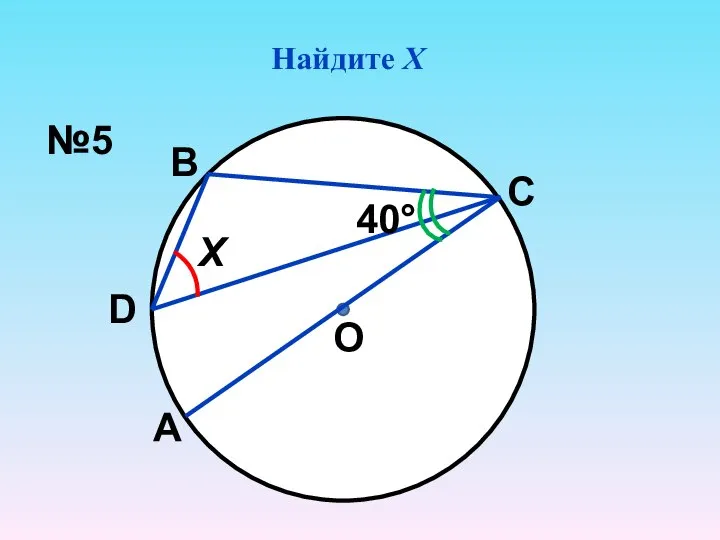
- 6. Найдите Х Х О 40° А D В С №5
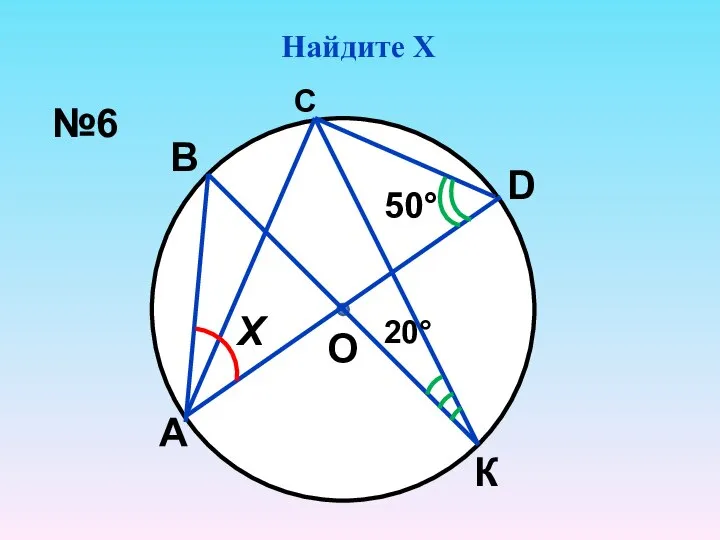
- 7. Найдите Х В К А D О С Х 50° 20° №6
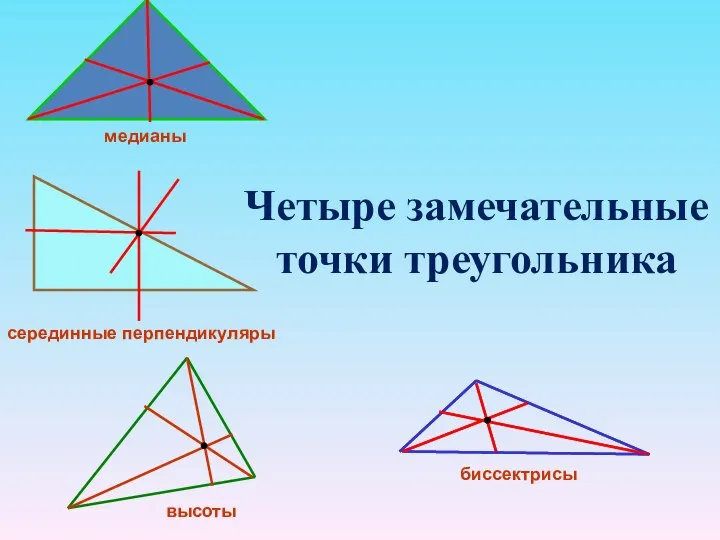
- 8. Четыре замечательные точки треугольника высоты биссектрисы серединные перпендикуляры медианы
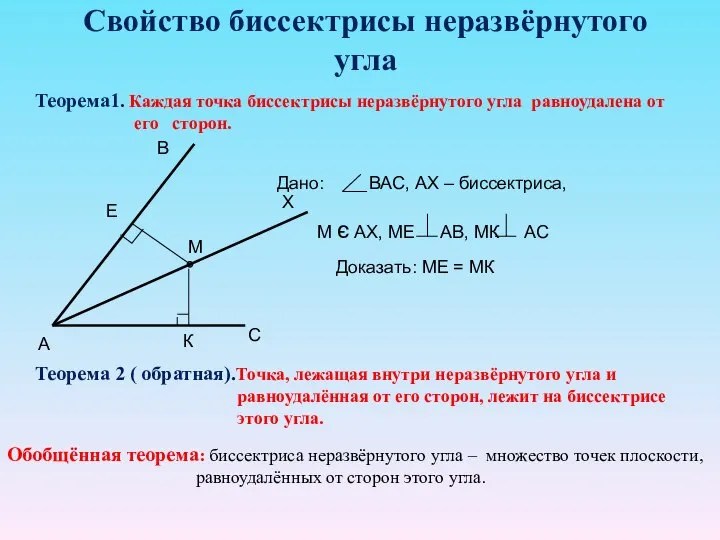
- 9. Свойство биссектрисы неразвёрнутого угла Теорема1. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Доказать: МЕ
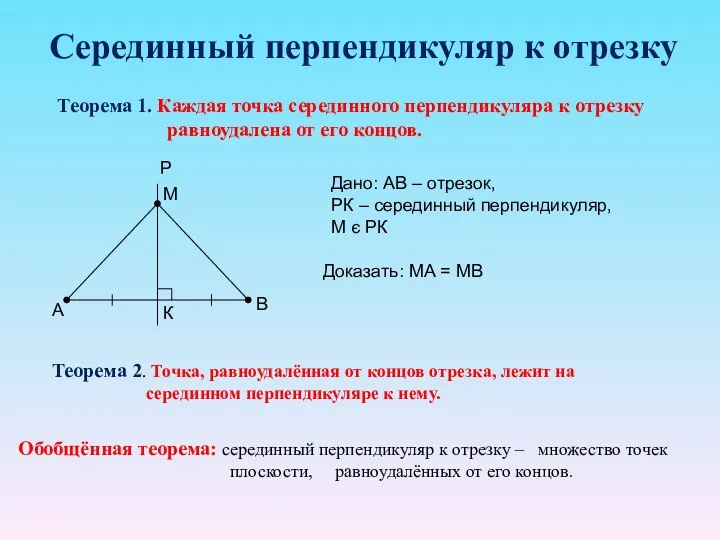
- 10. Серединный перпендикуляр к отрезку Теорема 1. Каждая точка серединного перпендикуляра к отрезку равноудалена от его концов.
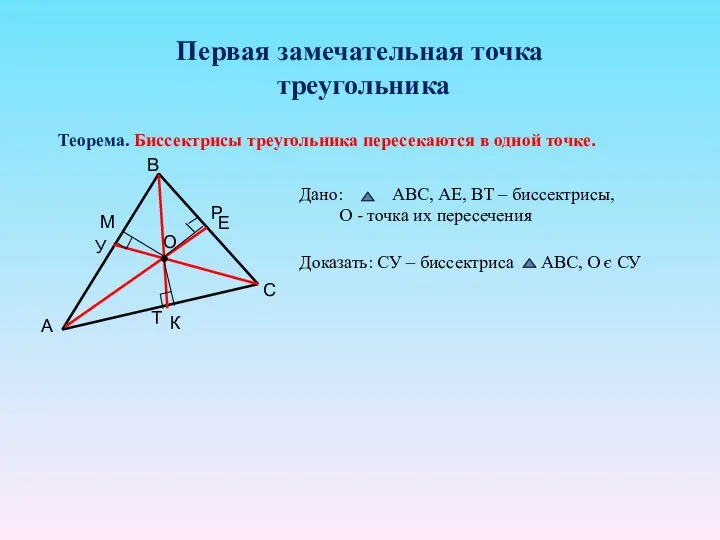
- 11. Первая замечательная точка треугольника Теорема. Биссектрисы треугольника пересекаются в одной точке.
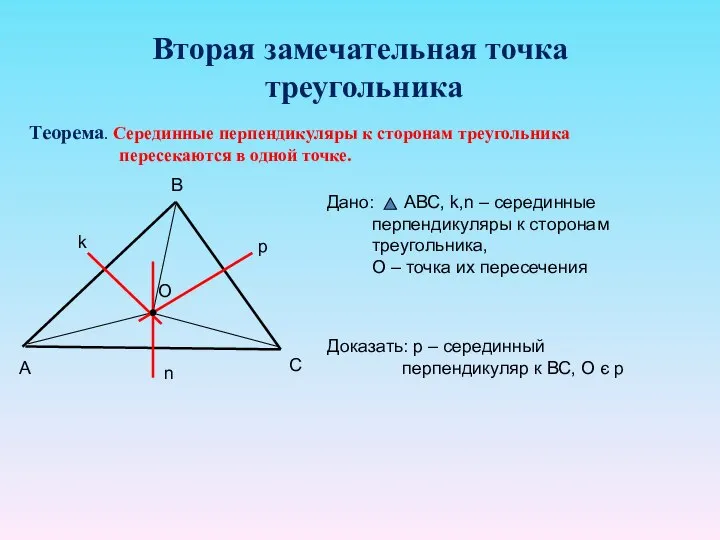
- 12. Вторая замечательная точка треугольника Теорема. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Доказать: р
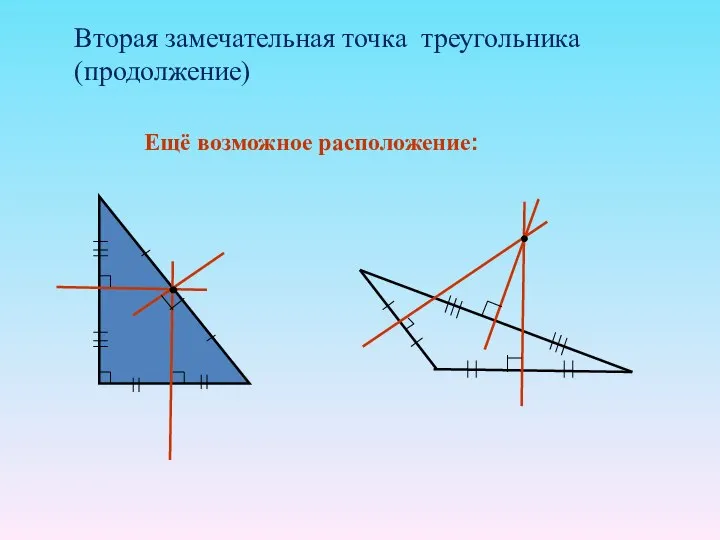
- 13. Вторая замечательная точка треугольника (продолжение) Ещё возможное расположение:
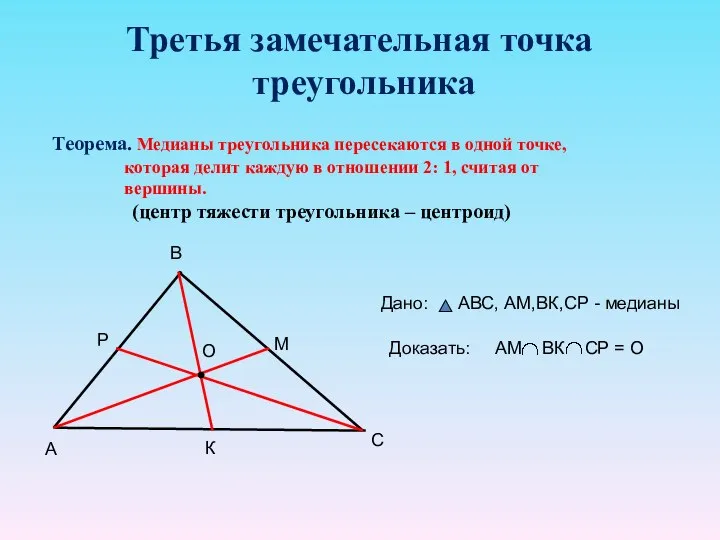
- 14. Третья замечательная точка треугольника Теорема. Медианы треугольника пересекаются в одной точке, которая делит каждую в отношении
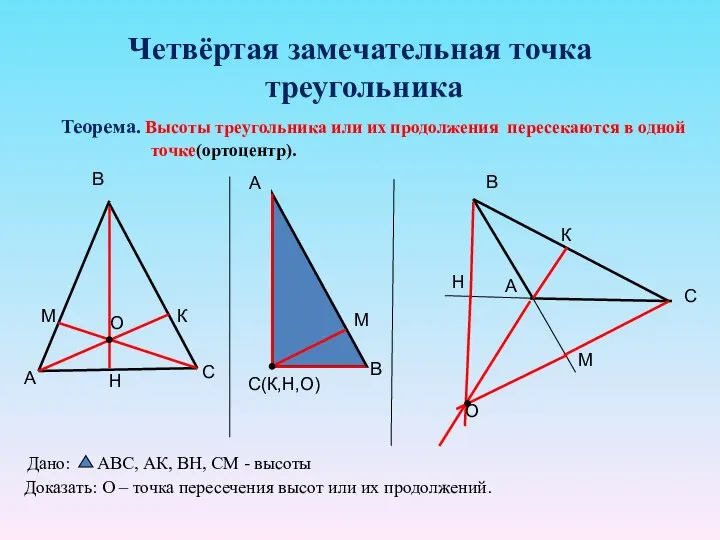
- 15. Четвёртая замечательная точка треугольника Теорема. Высоты треугольника или их продолжения пересекаются в одной точке(ортоцентр).
- 17. Скачать презентацию
 Смежные и вертикальные углы. Решение задач
Смежные и вертикальные углы. Решение задач Угол. Виды углов. Как образовалась эта фигура?
Угол. Виды углов. Как образовалась эта фигура? Живые числа (старшая группа, образовательная область познание)
Живые числа (старшая группа, образовательная область познание) Решение практико - ориентированных задач. Задачи про форматы листов
Решение практико - ориентированных задач. Задачи про форматы листов Вычисление интегралов средствами MathCad
Вычисление интегралов средствами MathCad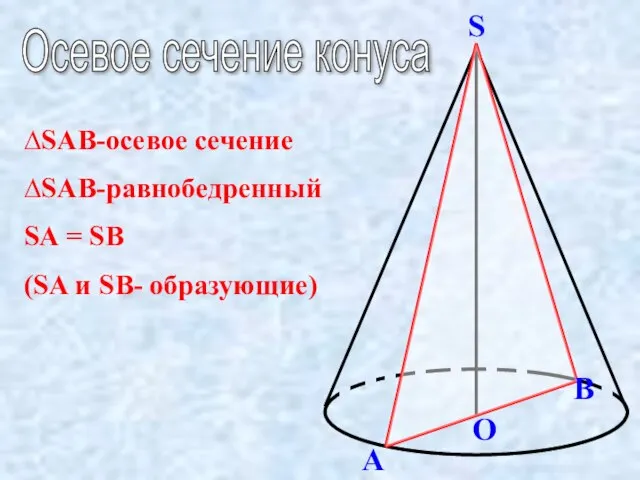 Осевое сечение конуса и цилиндра
Осевое сечение конуса и цилиндра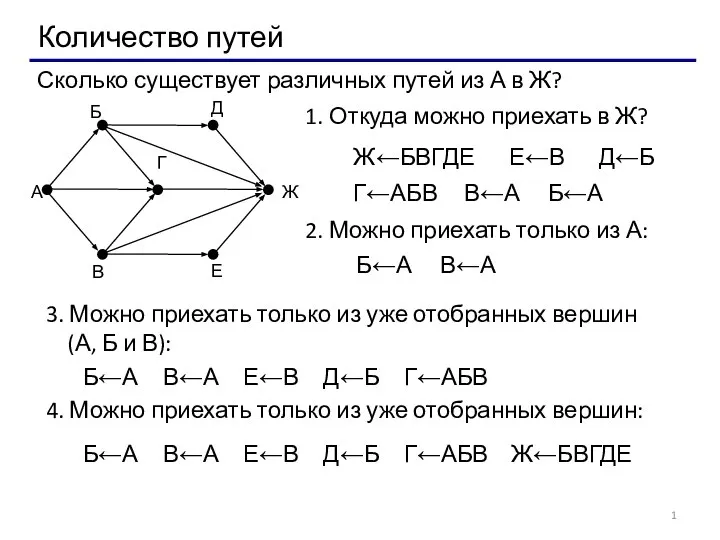 Количество путей из пункта А в Ж
Количество путей из пункта А в Ж Решение логарифмических уравнений
Решение логарифмических уравнений Прямопропорциональные величины
Прямопропорциональные величины Двугранный угол. Угол между плоскостями
Двугранный угол. Угол между плоскостями Математический марафон. Интеллектуальная игра
Математический марафон. Интеллектуальная игра Задача 6.15 из сборника задач к начальному курсу эконометрики
Задача 6.15 из сборника задач к начальному курсу эконометрики Определение общего числа единиц (десятков, сотен) в числе. 3 класс
Определение общего числа единиц (десятков, сотен) в числе. 3 класс Презентация на тему Игра "О, счастливчик, юный математик"
Презентация на тему Игра "О, счастливчик, юный математик"  ug_skal
ug_skal Задание 3(профиль) 8 (база)
Задание 3(профиль) 8 (база) Корень уравнения
Корень уравнения Путешествие в звездную математическую страну
Путешествие в звездную математическую страну Виды треугольников
Виды треугольников Четные и нечетные функции. 10 класс
Четные и нечетные функции. 10 класс Таблица сложения
Таблица сложения 04_8класс_Эталоны контроля качества продуктов труда. Измерительные приборы
04_8класс_Эталоны контроля качества продуктов труда. Измерительные приборы Загадки и тайны треугольника
Загадки и тайны треугольника Хочу все знать. Ломаные числа
Хочу все знать. Ломаные числа Решение квадратного уравнения в общем виде
Решение квадратного уравнения в общем виде Презентация на тему РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ  Презентация на тему Решение показательных уравнений 11 класс
Презентация на тему Решение показательных уравнений 11 класс