Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника

Выполните тест
https://edu.skysmart.ru/student/pimevekuke

Перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на этой прямой. Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

Теорема (о перпендикуляре к прямой).
В
А
Дано:
Доказать:
1) Существование перпенди-куляра к а.
Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
С
А∉ ВС.
2) Единственность такого перпендикуляра.

I. Существование перпендикуляра.

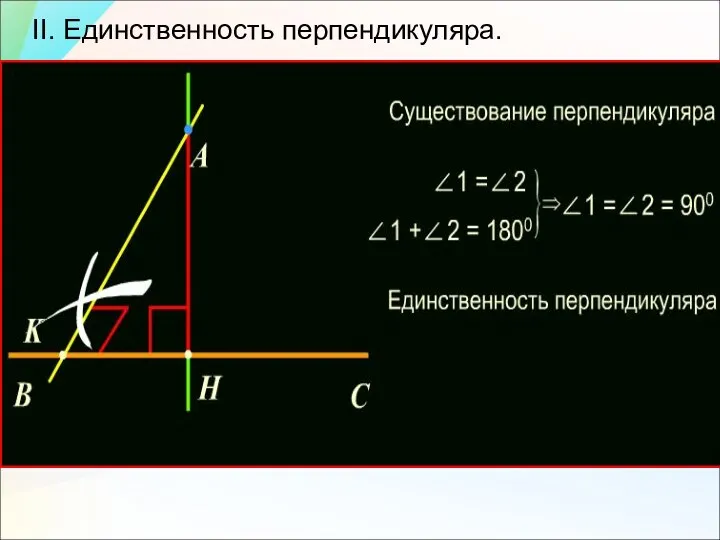
II. Единственность перпендикуляра.

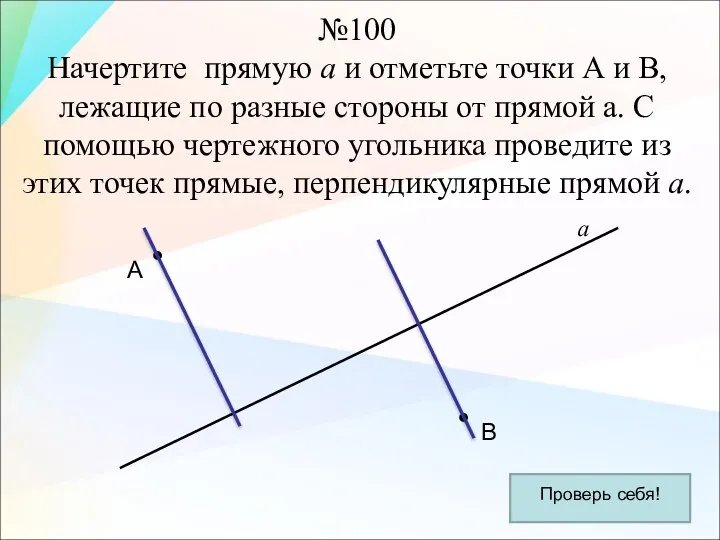
№100
Начертите прямую а и отметьте точки А и В, лежащие по разные стороны от прямой а. С помощью чертежного угольника проведите из этих точек прямые, перпендикулярные прямой а.
.
.
А
В
а

Медианы, биссектрисы
и высоты треугольника

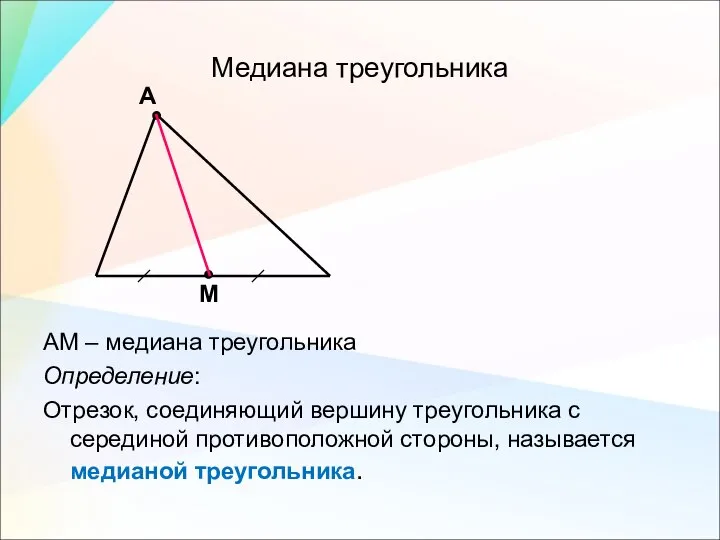
Медиана треугольника
АМ – медиана треугольника
Определение:
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
.
.
А
М

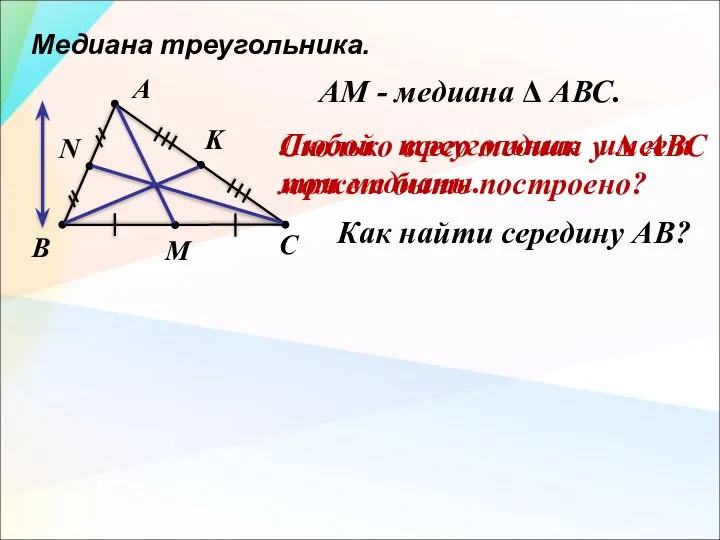
Медиана треугольника.
А
АМ - медиана Δ АВС.
В
С
М
Сколько всего медиан у Δ АВС может быть построено?
Любой треугольник имеет три медианы.
Как найти середину АВ?
N
K

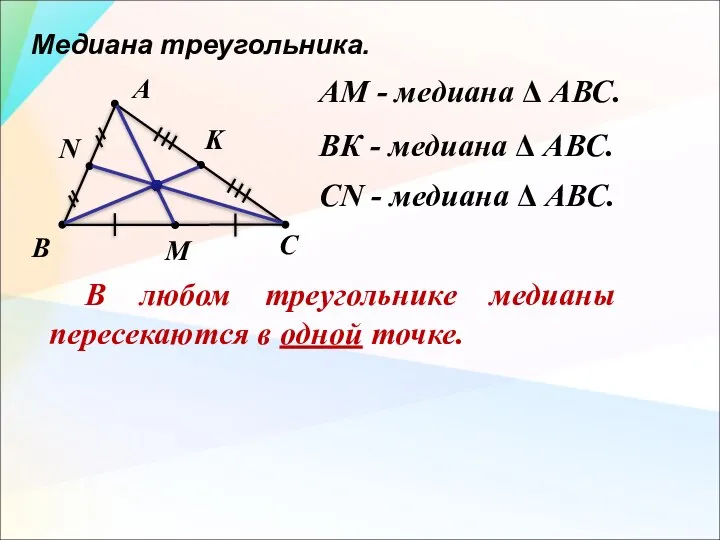
Медиана треугольника.
А
АМ - медиана Δ АВС.
В
С
М
N
K
ВК - медиана Δ АВС.
CN - медиана Δ АВС.
В любом треугольнике медианы пересекаются в одной точке.

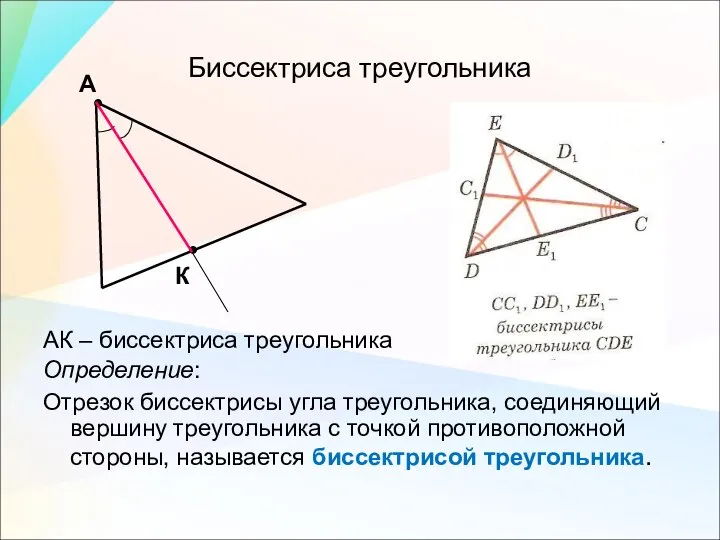
Биссектриса треугольника
АК – биссектриса треугольника
Определение:
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
.
.
А
К

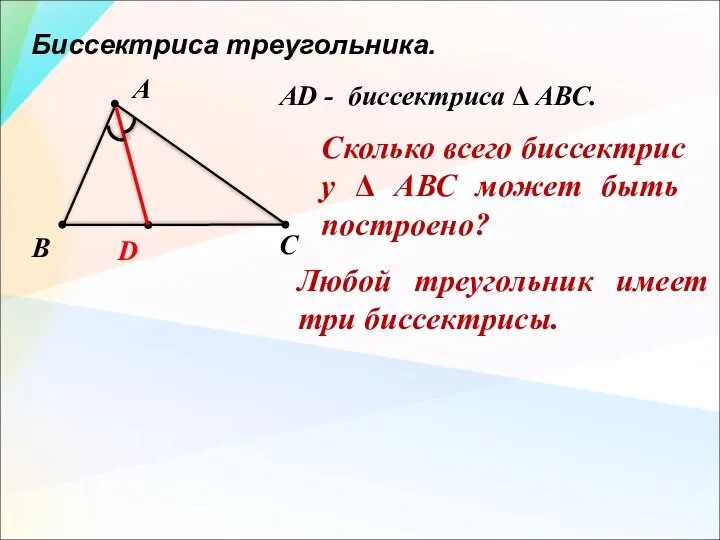
Биссектриса треугольника.
А
В
С
D
Любой треугольник имеет три биссектрисы.
Сколько всего биссектрис у Δ АВС может быть построено?
AD - биссектриса Δ АВС.

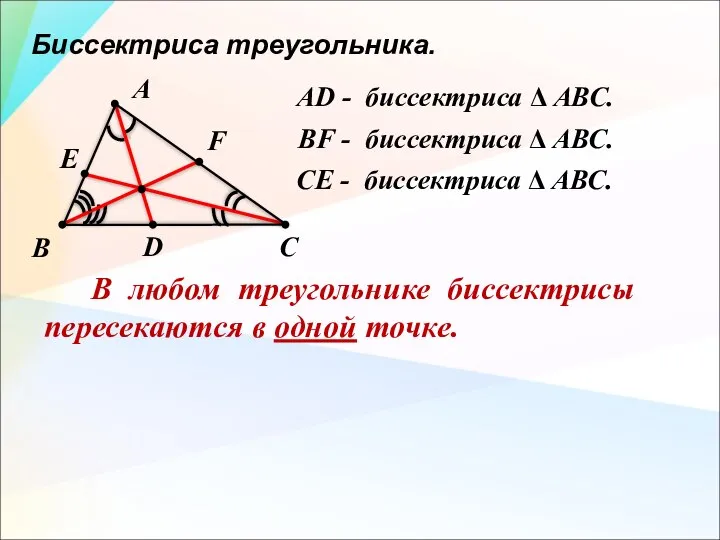
Биссектриса треугольника.
А
В
С
D
AD - биссектриса Δ АВС.
В любом треугольнике биссектрисы пересекаются в одной точке.
E
F
BF - биссектриса Δ АВС.
CE - биссектриса Δ АВС.

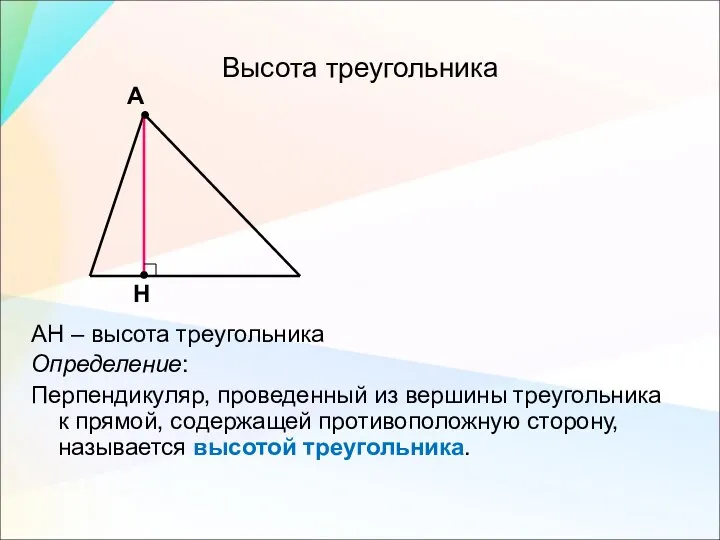
Высота треугольника
АН – высота треугольника
Определение:
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
.
.
А
Н

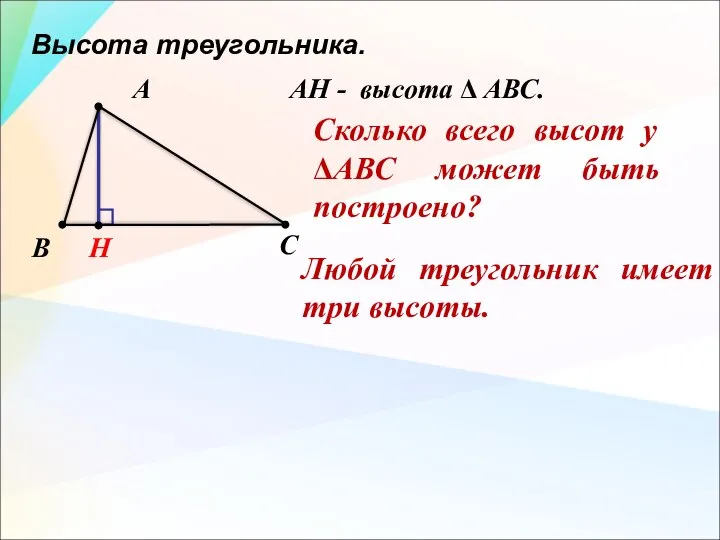
Высота треугольника.
А
В
С
Н
AН - высота Δ АВС.
Любой треугольник имеет три высоты.
Сколько всего высот у ΔАВС может быть построено?

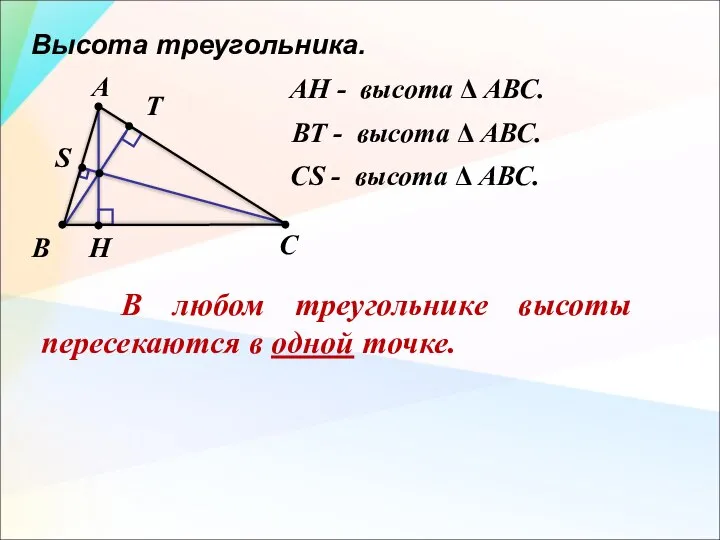
Высота треугольника.
А
В
С
Н
AН - высота Δ АВС.
S
T
ВТ - высота Δ АВС.
CS - высота Δ АВС.
В любом треугольнике высоты пересекаются в одной точке.

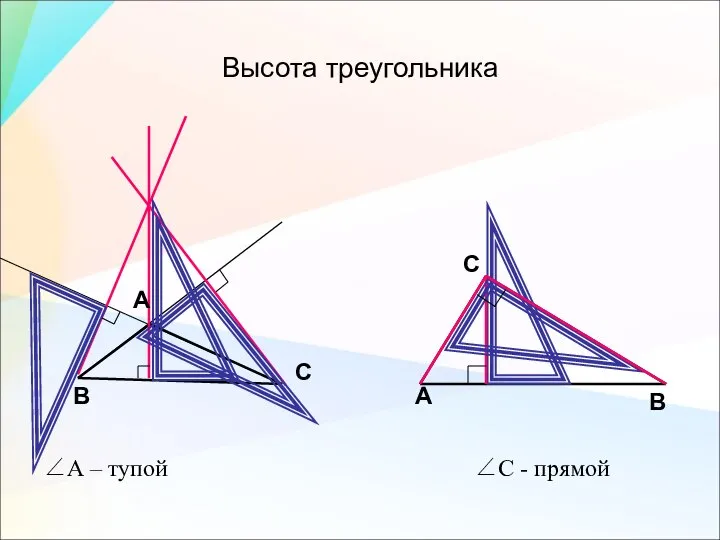
Высота треугольника
∠А – тупой ∠С - прямой
А
В
С
А
В
С

Решение задач

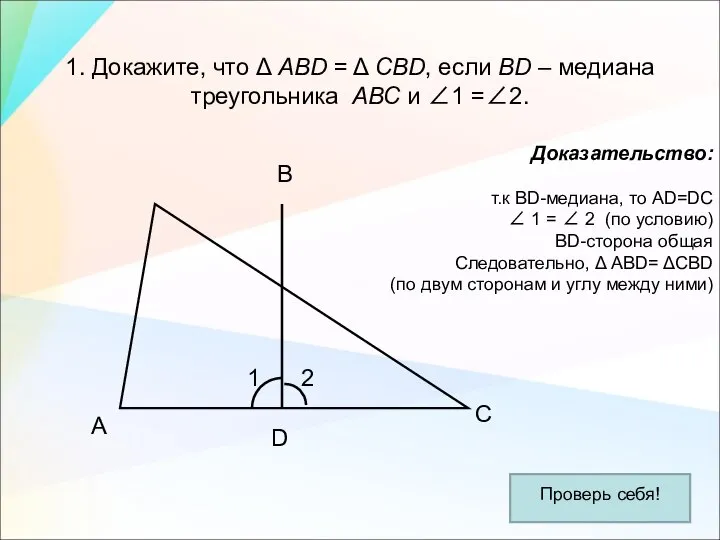
1. Докажите, что Δ АВD = Δ СВD, если ВD – медиана треугольника АВС и ∠1 =∠2.
А
D
С
В
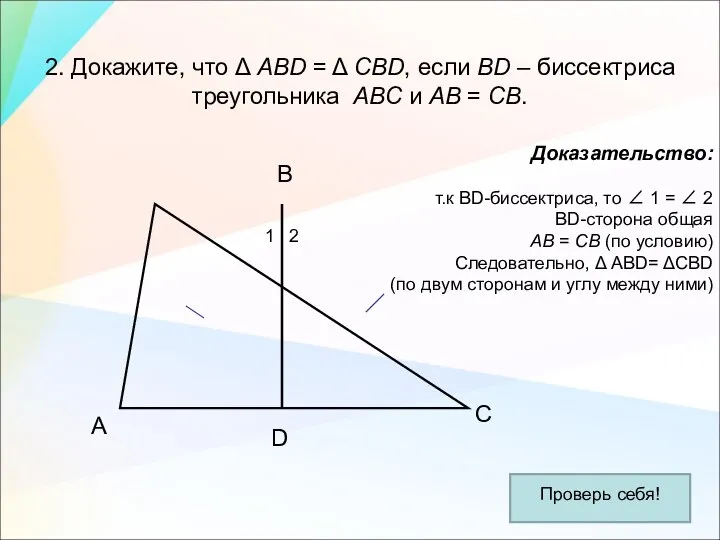
2
1

2. Докажите, что Δ АВD = Δ СВD, если ВD – биссектриса треугольника АВС и АВ = СВ.
А
D
С
В

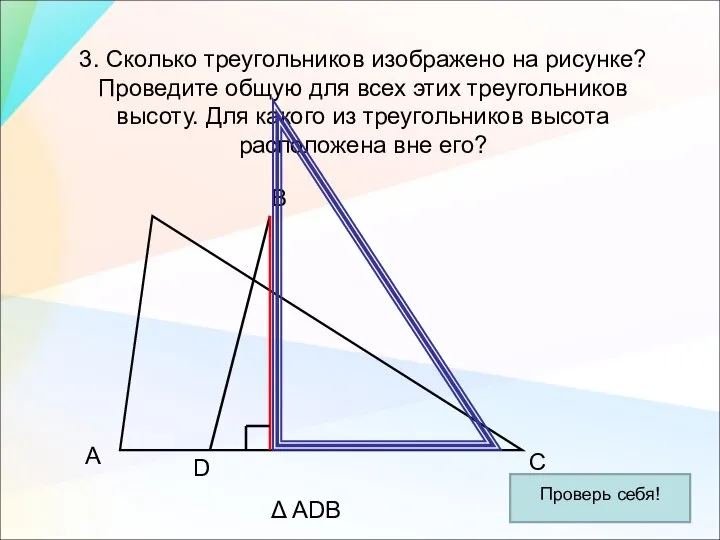
3. Сколько треугольников изображено на рисунке? Проведите общую для всех этих треугольников высоту. Для какого из треугольников высота расположена вне его?
D
В
А
С
Δ ADB

Домашнее задание
Начертите треугольник. С помощью масштабной линейки отметьте середины сторон и проведите медианы треугольника.
Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.
Начертите треугольник ABC с тремя острыми углами и треугольник MNP, у которого угол M тупой. С помощью чертежного треугольника проведите высоты каждого треугольника
Медиана AD треугольника ABC продолжена за точку D на отрезок DE, равный AD, и точка E соединена с точкой C.
-Докажите, что ΔABD= ΔECD.
-Найдите ∠ACE, если ∠ACD=56 , ∠ABD=40 .

Спасибо за работу

нет