Понятие множества

Понятие множества
Множество – это неопределяемое понятие.
Множество это объединение, совокупность, собрание объектов, объединённых общими свойствами.
Примеры:
Множество дней недели
Множество студентов в группе 1Н

Понятие элементов множества
Элементы множества – объекты, составляющие данное множество.
Примеры:
Множество – «множество дней недели».
Элемент множества – «вторник».
Не является элементом этого множества – «март».
А={1,2,3,4,5,6,7}, А∈5, А∉9.

Классификация множеств по количеству элементов
Конечные множества
Пример: А- «множество месяцев года», n(А)=12
Бесконечные множества
Пример: N – «множество натуральных чисел»
Пустые множества
Пример: В – «множество натуральных корней уравнения 3х+5=0», В={∅}, n(В)=0

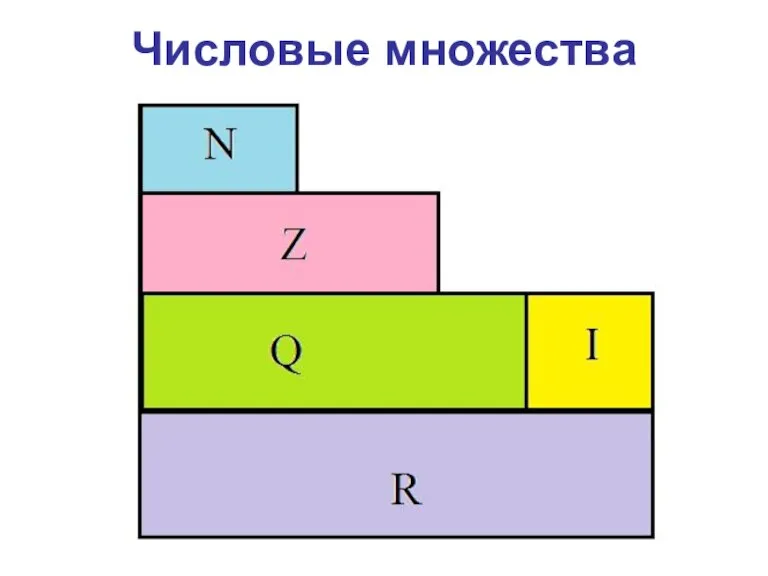
Числовые множества
N – множество натуральных чисел (1, 2, 3,…, 24,…, 57,…, 343564,…)
Z – множество целых чисел (…, -2, -1, 0, 1,2,…)
Q – множество рациональных чисел (…; - 4,6;…;⅔;…; 5; 6,7; …)
I – множество иррациональных чисел ( )
R – множество действительных чисел

Числовые множества

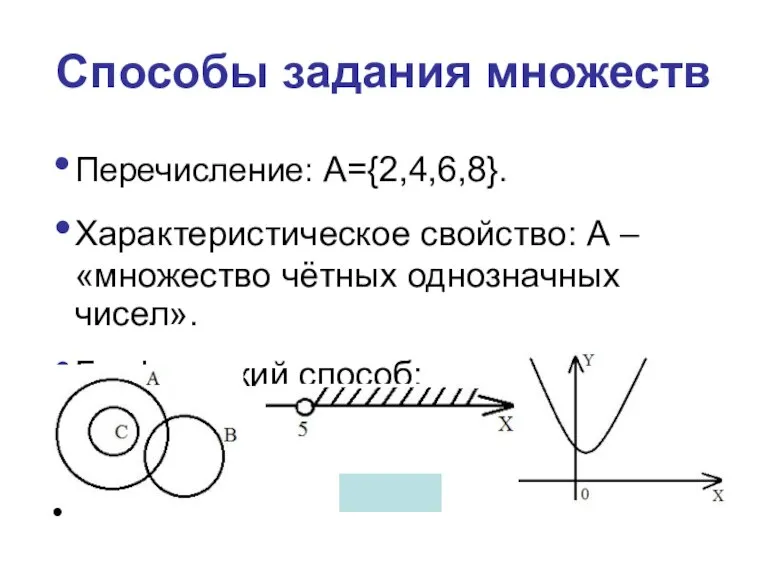
Способы задания множеств
Задать множество – это значит найти способ, позволяющий определить, принадлежит элемент данному множеству или не принадлежит.

Перечисление: А={2,4,6,8}.
Характеристическое свойство: А – «множество чётных однозначных чисел».
Графический способ:
Способы задания множеств