Содержание
- 2. Цели: 1. Рассмотреть правила нахождения суммы, разности векторов, заданных координатами, умножения их на число; показать применения
- 3. План работы: Установи соответствие. Подготовительный этап – повторение основных понятий; Слайд 4 Рассмотреть правило нахождения суммы,
- 4. Установите соответствие Любая точка пространства может рассматриваться как … вектор Вектором Коллинеарными Сонапрвленными и противоположно направленными
- 5. Сумма векторов. Правило треугольника Суммой векторов и называется вектор Правило треугольника. Для любых трех точек А,
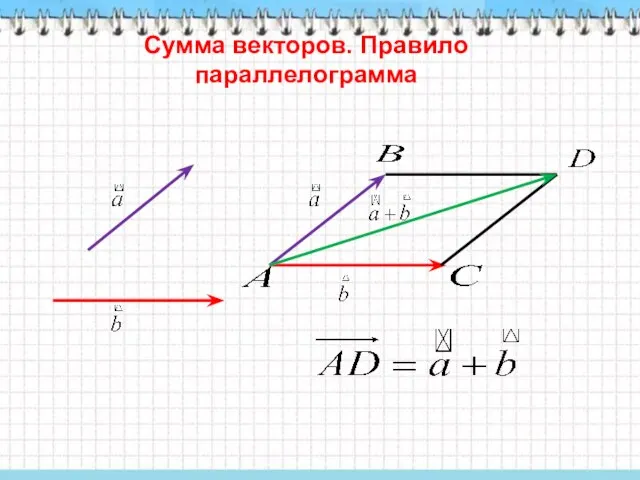
- 6. Сумма векторов. Правило параллелограмма
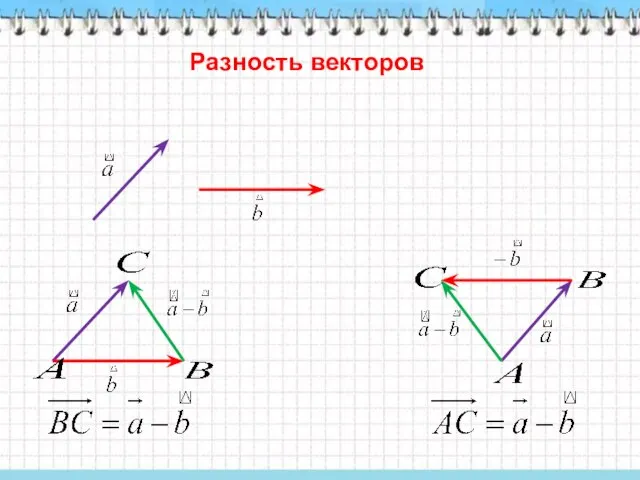
- 7. Разность векторов
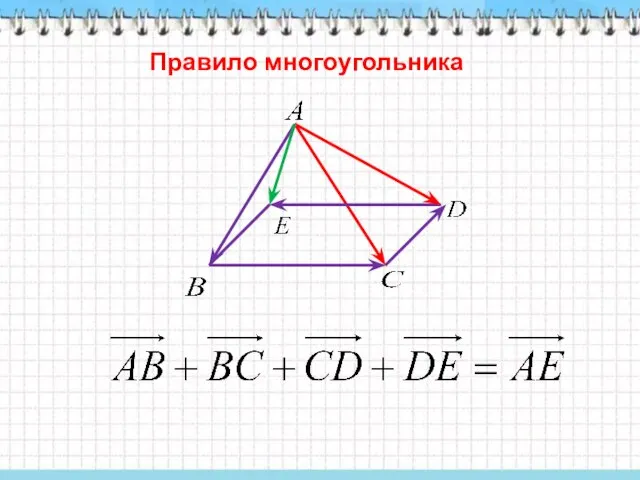
- 8. Правило многоугольника
- 9. Произведение вектора на число Произведением вектора на число называется вектор Абсолютная величина вектора равна ,а направление
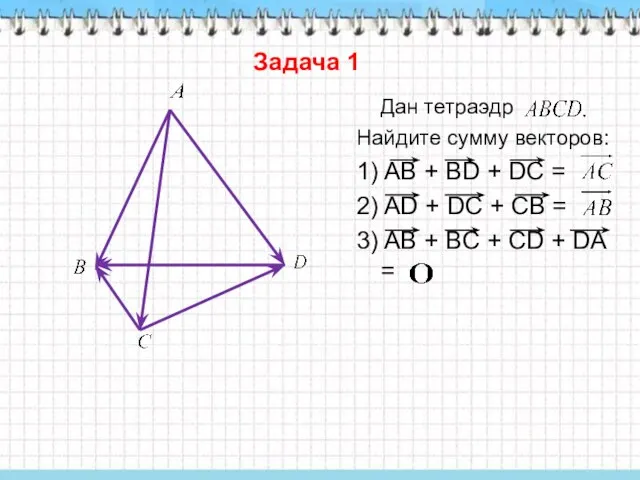
- 10. Задача 1 Дан тетраэдр Найдите сумму векторов: 1) AB + BD + DC = 2) AD
- 11. Задача 2 Дано: A (2;1;4), В (3;0;-1), С (1;-2;0). Найдите: 2 + 3 .
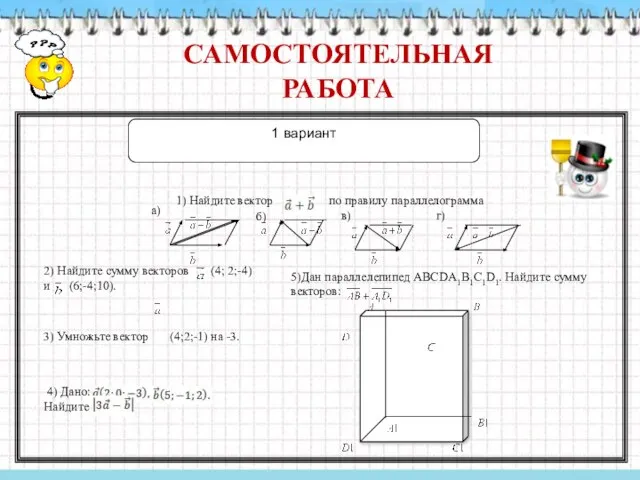
- 12. САМОСТОЯТЕЛЬНАЯ РАБОТА 1 вариант б) 1) Найдите вектор по правилу параллелограмма в) а) г) 2) Найдите
- 13. САМОСТОЯТЕЛЬНАЯ РАБОТА ОТВЕТЫ 1 вариант а. а +b (10; -2; 6). -3a (-12; -6; 3). .
- 15. Скачать презентацию







 Решение задач по теме Теорема Пифагора
Решение задач по теме Теорема Пифагора Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Путь и перемещение
Путь и перемещение Основные сведения о матрицах. Операции над матрицами
Основные сведения о матрицах. Операции над матрицами Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах
Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 Делители числа
Делители числа Золотое сечение
Золотое сечение Найдите производную функции. Практическая работа
Найдите производную функции. Практическая работа Число Пи
Число Пи Движение
Движение Способ группировки
Способ группировки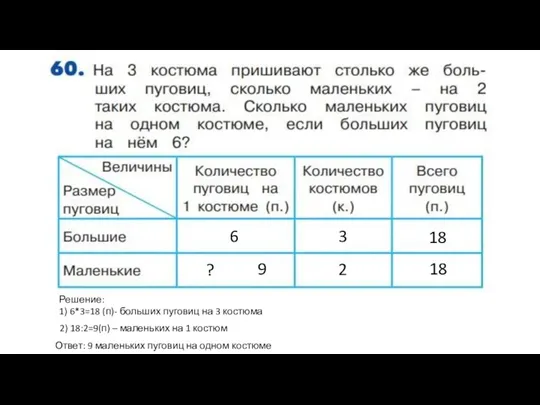 Задача о костюмах
Задача о костюмах Л11 Производная функции
Л11 Производная функции Задачи. Самостоятельная работа
Задачи. Самостоятельная работа Частное целых чисел. 6 класс
Частное целых чисел. 6 класс Исчисление высказываний
Исчисление высказываний Сложение чисел с переходом через десяток в пределах 20
Сложение чисел с переходом через десяток в пределах 20 Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 Умножение одночлена на многочлен
Умножение одночлена на многочлен Площади поверхностей и объёмы тел вращения
Площади поверхностей и объёмы тел вращения Октаэдр
Октаэдр В мире цветов и плодов. Интегрированный урок биологии и математики
В мире цветов и плодов. Интегрированный урок биологии и математики Золотой треугольник и много интересного
Золотой треугольник и много интересного Презентация на тему Масштаб и его практическое применение
Презентация на тему Масштаб и его практическое применение  Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Симетричні фігури
Симетричні фігури Математические головоломки и игры
Математические головоломки и игры