Декартова система координат в евклидовом пространстве

1-51
Правило буравчика
(правило правого винта)
Правая тройка векторов
Направление обхода -
против часовой стрелки
Левая тройка векторов = >

РАЗДЕЛ 1. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ

РАЗДЕЛ 2. ПРЯМАЯ В ПРОСТРАНСТВЕ
• Условия параллельности прямых
• Условия перпендикулярности прямых

РАЗДЕЛ 3. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ

Карл Фридрих Гаусс - родился 30 апреля 1777 года в Германии.
Считается "королем математики".
Занимался исследованиями в таких областях как:
алгебра, дифференциальная и неевклидовая геометрия, математический анализ, теории функций комплексного
переменного, теория вероятностей.

Р е ш е н и е

РАЗДЕЛ 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Поверхности второго порядка – это поверхности, уравнения которых в прямоугольной системе координат являются уравнениями второго порядка.
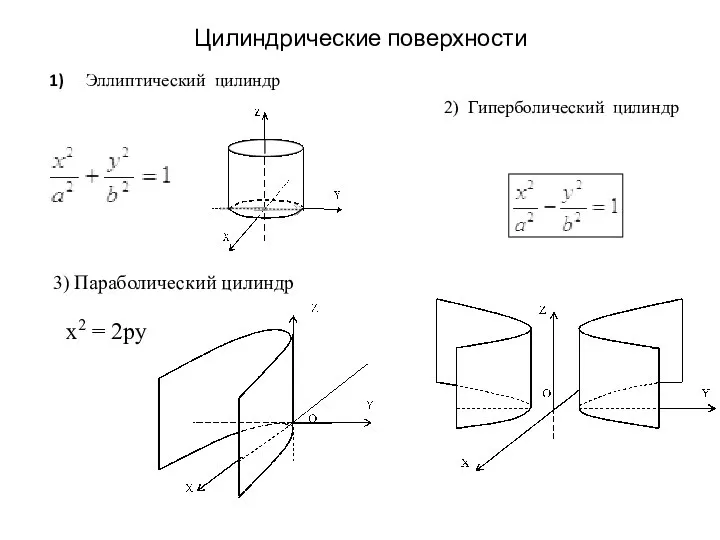
• Цилиндрические поверхности.
Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой.
Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т.е. направляющие параллельны оси Оz. Тип линии на плоскости ХOY (эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих:

Цилиндрические поверхности
Эллиптический цилиндр
2) Гиперболический цилиндр
3) Параболический цилиндр
x2 = 2py

Поверхности вращения

3) Однополостный гиперболоид:
2) Трехосный эллипсоид:

Двуполостный гиперболоид:
Конус второго порядка: