Декартово произведение множеств. Лекция №5

Отношение – представляет собой подмножество декартова произведения доменов.
Домен – это некоторое множество элементов или допустимых значений, которое может принимать объект по некоторому свойству.

Декартовым произведением доменов
где называется множество всех кортежей длинны n, т.е. состоящих из n элементов – по одному из каждого домена .
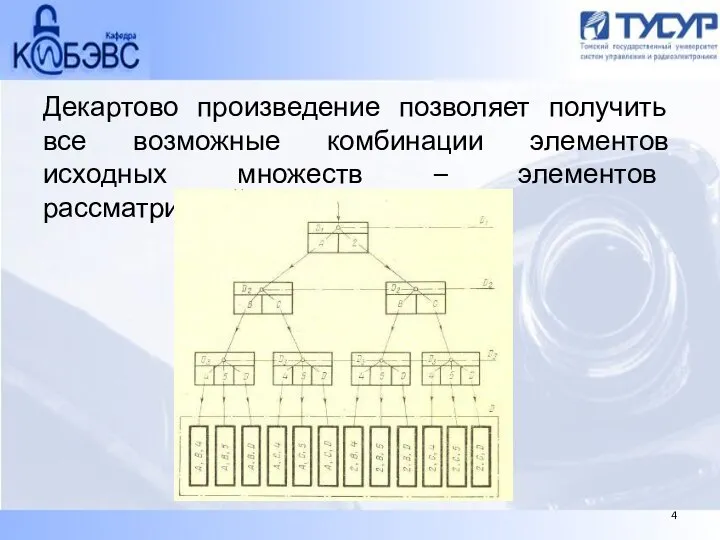
4

Декартово произведение позволяет получить все возможные комбинации элементов исходных множеств – элементов рассматриваемых доменов.
4

Отношением R – на множествах называется подмножество декартова произведения
Отношение R, определенное на множествах
есть некоторое множество кортежей арности n: , таких что принадлежит ,
- и т.д.:
4

Элементами отношений являются кортежи.
Арность кортежа определяется арностью отношения. Отношение арностью 1 называют – унарными, арности 2 – бинарными, арности 3 – тернарными, арности n – n-арными.
Замечание: поскольку отношение – это множество, то:
не должны встречаться одинаковые кортежи;
порядок кортежей в отношении не существенен.
4

Отношения удобно представлять через таблицу, где каждая строка это – кортеж, а каждый столбец соответствует одному и тому же компоненту декартова произведения, т.е. в нем могут появляться только элементы из соответствующего домена.
4

Таблица представляющая n-арное отношение, обладает следующими свойствами:
каждая строка представляет собой кортеж из n значений, принадлежащих n столбцам;
порядок столбцов фиксирован: (1,2,…, n);
порядок строк безразличен;
любые две строки различаются хотя бы одним элементом;
строки и столбцы могут обрабатываться в любой последовательности, определяемой применяемыми операциями обработки.
1. По типу управляемой базы данных СУБД.
2. По архитектуре СУБД и организации хранения данных.
3. По способу доступа СУБД к базе данных.
4

При определении теоретико-множественного отношения предполагает работу с линейными списками при обработке данных. Такая форма удобна для операций реляционной алгебры.
Однако она не всегда целесообразна из-за фиксированного порядка столбцов в отношении, т.к. в ряде приложений возникает необходимость перестановки столбцов в отношении в любом порядке.

Необходимости фиксированного порядка столбцов в отношении столбцы именуют что делает их порядок в отношении не существенным .
Столбцы отношения, с присвоенными им именами, называют атрибутами.
Список имен атрибутов отношения называют схемой отношения.
4

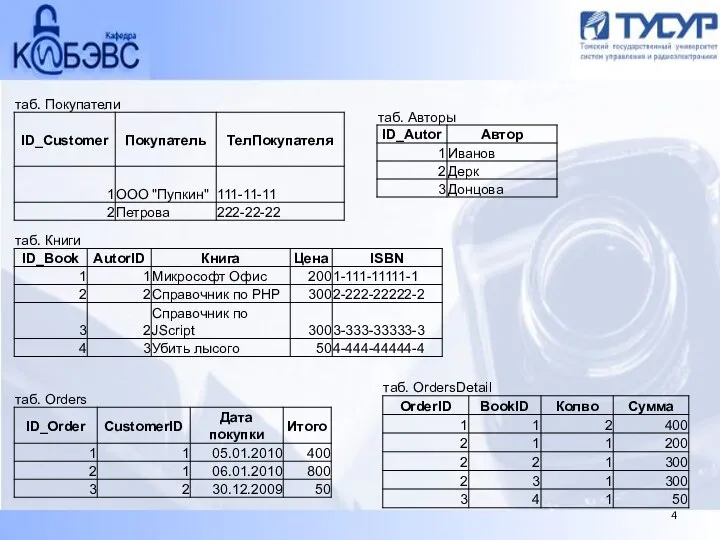
Существует аналогия между схемой отношения и форматом записи, между кортежем и записью, между отношением и файлом.
Следствием этого является возможная реализация отношения в виде файла записей, формат которых соответствует схеме отношения.
4

Реляционная база данных – это набор экземпляров конечных отношений.
Схема реляционной БД представляется в виде совокупности схем отношений
4

Нормализация
4

Нормализация – процесс реорганизации данных путем ликвидации повторяющихся групп и иных противоречий в хранении данных с целью приведения таблиц к виду позволяющему осуществлять непротиворечивое и корректное редактирование данных.
4

1ая нормальная форма
Для того чтобы таблица соответствовала 1НФ все значения ее полей должны быть атомарными а записи уникальными.
Значения доменов рассматриваются как не делимые, а не как множества или кортежи из более элементарных доменов.
4

4

4

2ая нормальная форма
Таблица находиться во 2НФ, если она находиться в 1НФ и ее не ключевые поля полностью зависят от всего первичного ключа, не являясь его частью.
4

4

4

3ья нормальная форма
Таблица находиться в 3НФ, если она находиться во 2 НФ и ни одно из неключевых полей не определяет другое не ключевое поле.
Отношение имеет только один ключ и другие зависимости, в том числе многозначные
4

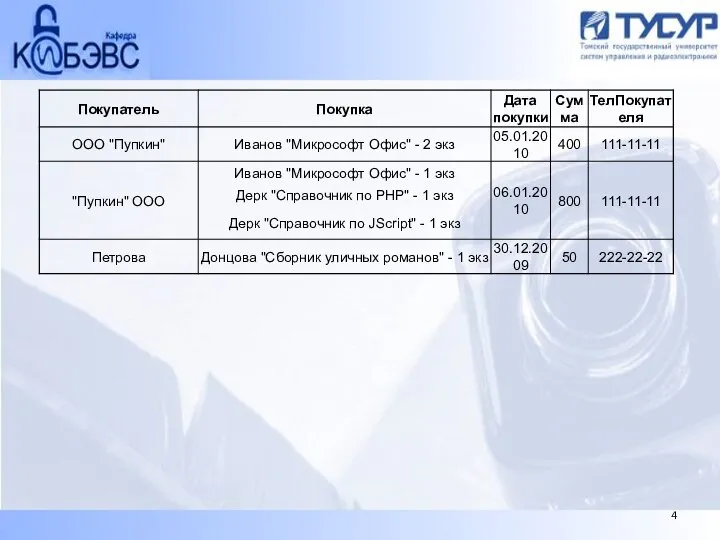
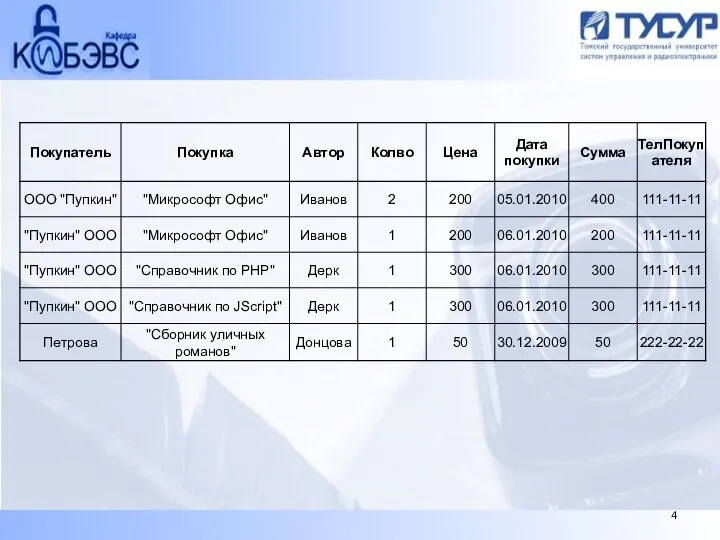
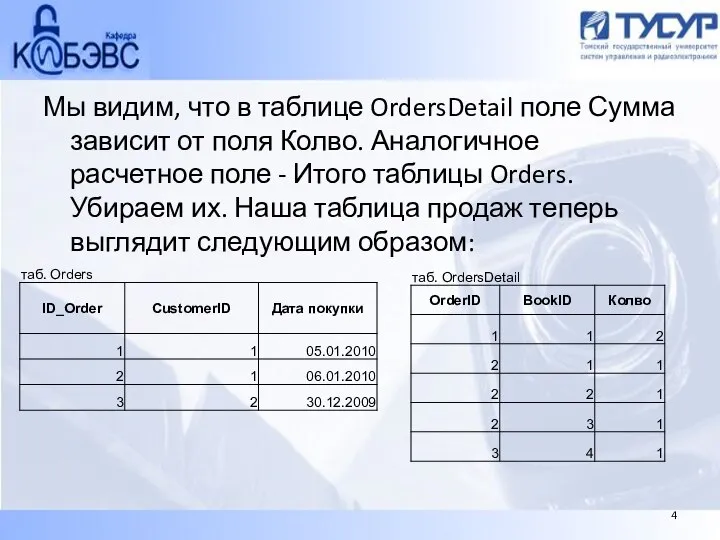
Мы видим, что в таблице OrdersDetail поле Сумма зависит от поля Колво. Аналогичное расчетное поле - Итого таблицы Orders. Убираем их. Наша таблица продаж теперь выглядит следующим образом:
4

Нормальная форма Бойса-Кода
Детерминант а – это атрибут (или комбинация атрибутов) от которого другой атрибут зависит функционально (полно).
В этом случае отношение R находиться в БКНФ, если каждая детерминанта является возможным ключом.
4

Существует отношение:
(Номер зачетной книжки, идентификатор студента, дисциплина, дата, оценка)
БКНФ:
(Идентификатор студента, дисциплина, дата, оценка)
(Номер зачетной книжки, идентификатор студента)
Или
(Номер зачетной книжки, дисциплина, дата, оценка)
(Номер зачетной книжки, идентификатор студента)

4ая нормальная форма
4НФ запрещает хранить независимые компоненты в одной таблице, когда между этими компонентами существуют отношение многие-ко-многим.
4

Существует отношение:
(Номер зачетной книжки, группа, дисциплина)
4НФ:
(группа - дисциплина)
(группа – номер зачетной книжки)