Дифференциальные уравнения

Дифференциальное уравнение
Уравнение, в которое входят производные функции, и может входить сама функция, независимая переменная и параметры. Порядок входящих в уравнение производных может быть различен.

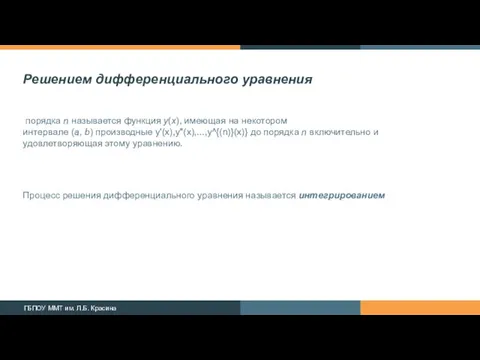
Решением дифференциального уравнения
порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y'(x),y''(x),...,y^{(n)}(x)} до порядка n включительно и удовлетворяющая этому уравнению.
Процесс решения дифференциального уравнения называется интегрированием

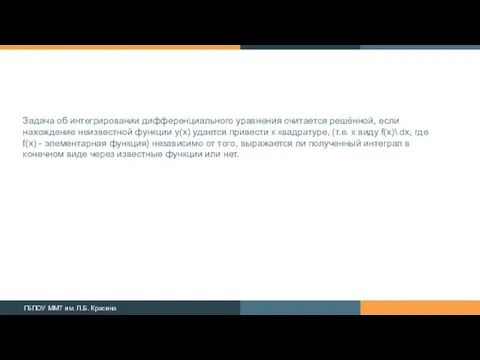
Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции y(x) удается привести к квадратуре, (т.е. к виду f(x)\ dx, где f(x) - элементарная функция) независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.

Виды дифференциальных уравнений
Обыкновенные
Уравнения с частными производными
Стохастические дифференциальные уравнения

Обыкновенные (ОДУ)
это дифференциальные уравнения для функции от одной переменной.
Они имеют вид:

Уравнения с частными производными
это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные
Общий вид:

Стохастическое дифференциальное уравнение (СДУ)
Уравнение ,в котором один член или более имеют стохастическую природу, то есть представляют собой стохастический процесс. Таким образом, решения уравнения также оказываются стохастическими процессами.
В физике СДУ традиционно записывают в форме уравнения Ланжевена.
И часто, не совсем точно, называют самим уравнением Ланжевина, хотя СДУ можно записать многими другими способами.
СДУ первого порядка:

История дифференциальных уравнений
Первоначально дифференциальные уравнения возникли из задач механики, в которых требовалось определить координаты тел, их скорости и ускорения, рассматриваемые как функции времени при различных воздействиях. К дифференциальным уравнениям приводили также некоторые рассмотренные в то время геометрические задачи.

Основой теории дифференциальных уравнений стало дифференциальное исчисление, созданное Лейбницем и Ньютоном. Сам термин «дифференциальное уравнение» был предложен в 1676 году Лейбницем.

Из огромного числа работ по дифференциальным уравнениям выделяются работы Эйлера и Лагранжа. В этих работах была прежде развита теория малых колебаний, а следовательно — теория линейных систем дифференциальных уравнений