Определение и содержание математического программирования как математической дисциплины

ИСТОРИЯ
Математическое программирование возникло в 30-е годы XX века. Венгерский математик Б.Эгервари в 1931 году решил задачу, называемую проблемой выбора. Американский ученый Г.У. Куй обобщил этот метод, после чего он получил название венгерского метода. В 1939 году российский ученый Л.В. Канторович разработал метод разрешающих множителей решения задач линейного программирования. Большой вклад в развитие математического программирования внесли американские ученые.

В 1939 году российский ученый Л.В. Канторович разработал метод разрешающих множителей решения задач линейного программирования. Большой вклад в развитие математического программирования внесли американские ученые.

МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ-
это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями.

Исследование различных процессов обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения.

Математическое программирование включает в себя такие разделы математики как линейное, нелинейное и динамическое программирование. Сюда же обычно относят стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.

ЭТАПЫ СОСТАВЛЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЭКОНОМИЧЕСКОЙ ЗАДАЧИ:
выбор переменных задачи;
составление системы ограничений;
выбор целевой функции.

Переменными задачи называются величины x1, x2, х3,..., xn, которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора X=(x1, x2, x3,…., xn)
Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.
Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.

Допустимым решением (планом) задачи линейного программирования называется любой n-мерный вектор X=(X1, X2,...,Xn), удовлетворяющий системе ограничений и условиям неотрицательности.
Множество допустимых решений (планов) задачи образует область допустимых решений (ОДР).
Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.

ЗАДАЧА 1:
Для производства продукции 2-х видов А и В используется материал трех сортов. Данные о затратах сырья на производство единицы продукции, запасах сырья и прибыли от реализации единицы продукции приведены в таблице:
Требуется составить такой план производства, при котором предприятие получит наибольшую прибыль

РЕШЕНИЕ:
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 4x1+6x2 при следующих условиях-ограничений.
4x1+x2≤196
8x1+7x2≤552
5x1+9x2≤567

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≤) вводим базисную переменную x3. В 2-м неравенстве смысла (≤) вводим базисную переменную x4. В 3-м неравенстве смысла (≤) вводим базисную переменную x5.
4x1+x2+x3 = 196
8x1+7x2+x4 = 552
5x1+9x2+x5 = 567

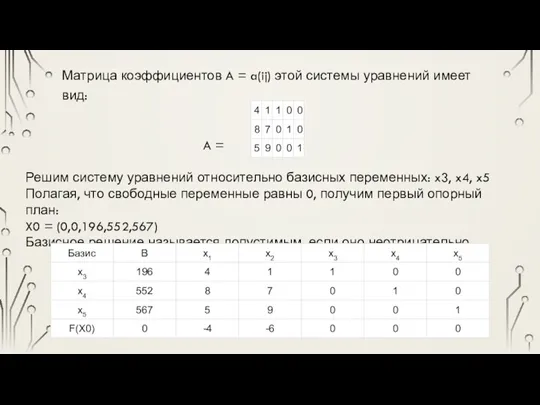
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
A =
Решим систему уравнений относительно базисных переменных: x3, x4, x5
Полагая, что свободные переменные равны 0, получим первый опорный план:
X0 = (0,0,196,552,567)
Базисное решение называется допустимым, если оно неотрицательно.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю.
Необходимо определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai2
и из них выберем наименьшее:
min (196 : 1 , 552 : 7 , 567 : 9 ) = 63
Следовательно, 3-ая строка является ведущей.
Разрешающий элемент равен (9) и находится на пересечении ведущего столбца и ведущей строки.

Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 1 войдет переменная x2.
Строка, соответствующая переменной x2 в плане 1, получена в результате деления всех элементов строки x5 плана 0 на разрешающий элемент РЭ=9. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули.
Таким образом, в новом плане 1 заполнены строка x2 и столбец x2. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.

Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
СТЭ - элемент старого плана, РЭ - разрешающий элемент (9), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.

Получаем новую симплекс-таблицу:
Получаем новую симплекс-таблицу

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю.
Вычислим значения Di по строкам как частное от деления: bi / ai1
и из них выберем наименьшее:
min (133 : 34/9 , 111 : 41/9 , 63 : 5/9 ) = 27
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (41/9) и находится на пересечении ведущего столбца и ведущей строки.

Формируем следующую часть симплексной таблицы. Вместо переменной x4 в план 2 войдет переменная x1.
Строка, соответствующая переменной x1 в плане 2, получена в результате деления всех элементов строки x4 плана 1 на разрешающий элемент РЭ=41/9. На месте разрешающего элемента получаем 1. В остальных клетках столбца x1 записываем нули.
Таким образом, в новом плане 2 заполнены строка x1 и столбец x1. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.

Представим расчет каждого элемента в виде таблицы:

Получаем новую симплекс-таблицу:
Получаем новую симплекс-таблицу:

Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Оптимальный план можно записать так:
x1 = 27, x2 = 48
F(X) = 4•27 + 6•48 = 396

ЗАДАЧА 2:
В районе имеются четыре ткацкие фабрики, выпускающие ткань определенного артикула. Для ее выпуска требуется два вида пряжи. По плану району отпускается 6000 и 4000 усл. ед. этих видов пряжи. В таблице приведен расход в единицу времени на каждой фабрике каждого вида пряжи и данные, характеризующие производительность (количество, ткани, изготовляемое на каждой фабрике в единицу времени).
Определить время работы каждой фабрики по выпуску ткани данного артикула так, чтобы при этом обеспечивался максимальный выпуск ткани. В соответствии с оптимальным планом распределить пряжу между фабриками.