Презентация на тему Четные и нечетные функции

Определение
Функция y=f (x) называется чётной, если:
D (f) симметрична относительно нуля;
2) для любого х Є D (f) верно равенство: f (-x) = f (x).
Функция y=f (x) называется нечётной, если:
1) D (f) симметрична относительно нуля;
2) для любого х Є D (f) верно равенство: f (-x) = - f (x).
Выяснить является ли функция чётной или нечётной:
y (х) = 5 x²- |X|
Решение: D (y) = R
y (- x)=
=5 (- x)² - |- x| =
= 5 x² - |x|=
= y (x)
Значит, функция - чётная
у(х) = 7x +x³
Решение: D (y) = R
y (- x)=
= 7(- x) +(- x)³=
= - 7 x - x³ =
= - (7x +x³)
= - y (x)
Значит, функция - нечётная

Функция f (x) – чётная,
f ( 3 ) = 25 , тогда f ( -3 ) = ?
f ( -8 ) = -71, тогда f ( 8 ) = ?
Функция g ( x ) – нечётная,
g ( 7 ) = 43, тогда g ( -7 ) = ?
g ( - 2 ) = -64, тогда g ( 2 ) = ?
25
-71
- 43
64

Существуют функции, которые не обладают
свойствами чётности или нечётности.
у (х) = х2 + 5х
у ( - х ) = ( - х)2 +5 (- х) = х2 – 5 х
Значит, данная функция не является ни чётной, ни нечётной.
D (y) = R

Является ли функция четной или нечетной?
чётная
нечётная
нечётная
чётная
ни чётная, ни нечётная

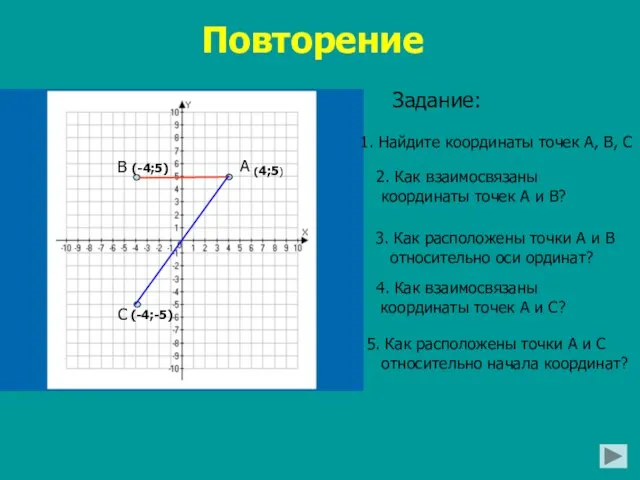
Повторение
Задание:
1. Найдите координаты точек А, В, С
2. Как взаимосвязаны
координаты точек А и В?
3. Как расположены точки А и В
относительно оси ординат?
4. Как взаимосвязаны
координаты точек А и С?
5. Как расположены точки А и С
относительно начала координат?

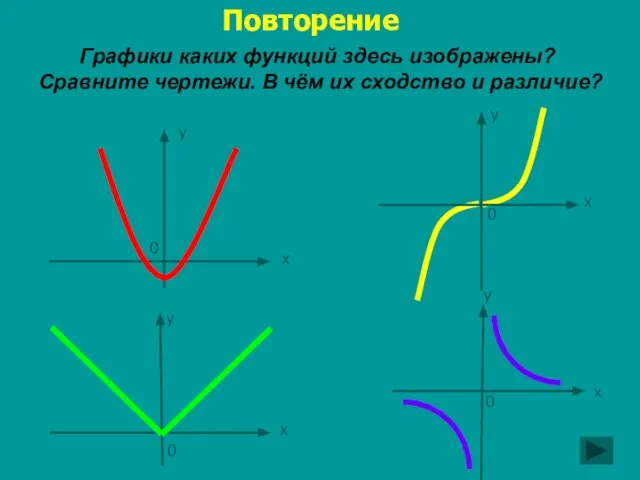
Графики каких функций здесь изображены?
Сравните чертежи. В чём их сходство и различие?
Повторение

Свойство графиков
чётных функций
По определению:
если функция – чётная, то противоположным значениям х
соответствуют равные значения у.
Сделайте вывод: 1) об области определения функции;
2) о расположении точек графика чётной функции.
Вывод: 1) область определения симметрична относительно точки (0; 0);
2) график чётной функции состоит из точек, симметричных
относительно оси ординат.
График чётной функции симметричен
относительно оси ординат.

Свойство графиков
нечётных функций
По определению:
если функция – нечётная, то противоположным значениям х
соответствуют противоположные значения у.
Сделайте вывод: 1) об области определения функции;
2) о расположении точек графика нечётной функции.
Вывод:1) область определения симметрична относительно точки (0; 0);
2)график нечётной функции состоит из точек, симметричных
относительно начала координат.
График нечётной функции симметричен
относительно начала координат.

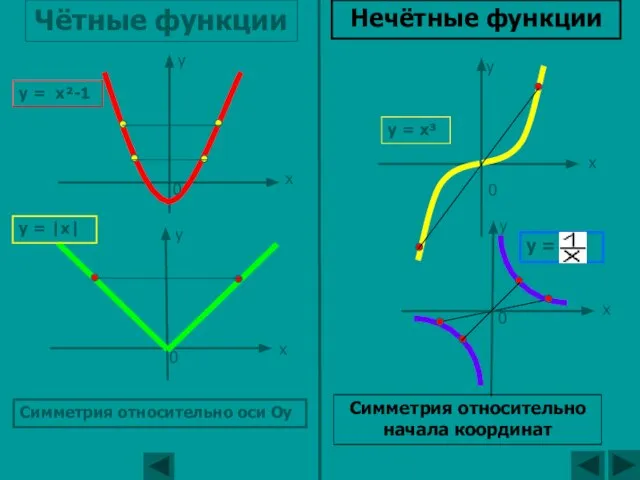
y = x²-1
y = |x|
y = x³
y =
Чётные функции
Нечётные функции
Симметрия относительно оси Оy
Симметрия относительно
начала координат
х
х
х
х
у
у
у
у
0
0
0
0

Может ли быть четной или нечетной функция,
областью определения которой является:
а) промежуток [ -2; 5 ]
б) промежуток ( -5; 5 )
в) промежуток ( -3; 3 ]
г) объединение промежутков
[ -10; -2] и [ 2; 10 ]
нет
да
нет
да

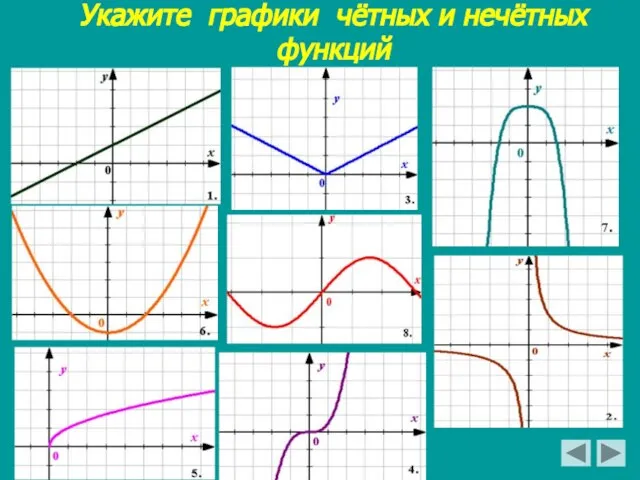
Укажите графики чётных и нечётных функций

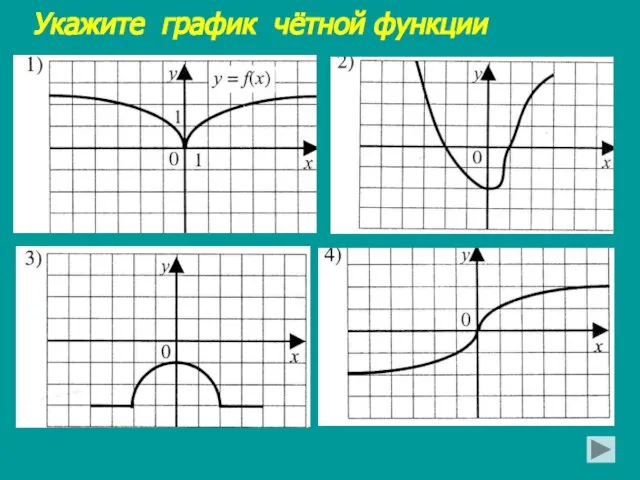
Укажите график чётной функции

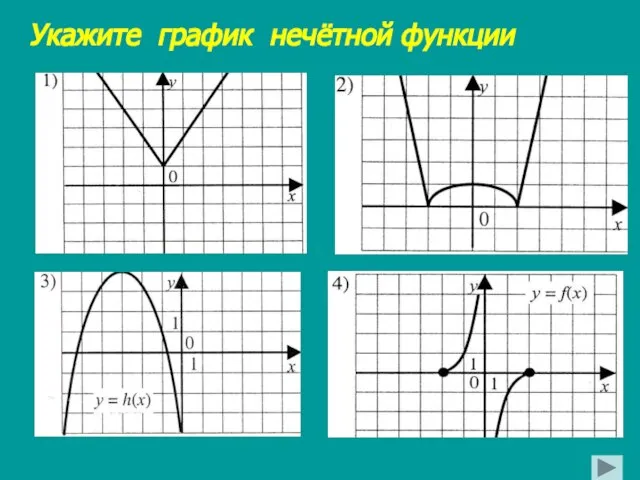
Укажите график нечётной функции

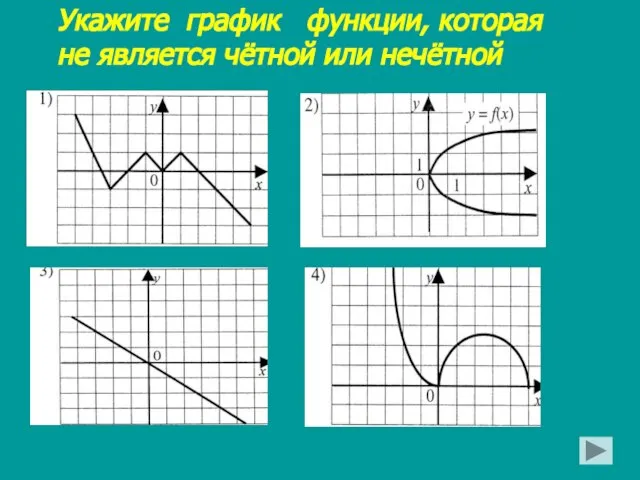
Укажите график функции, которая
не является чётной или нечётной

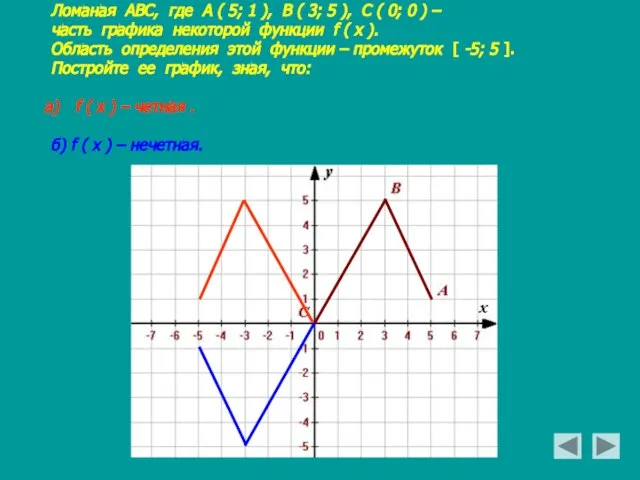
Ломаная АВС, где А ( 5; 1 ), В ( 3; 5 ), С ( 0; 0 ) –
часть графика некоторой функции f ( x ).
Область определения этой функции – промежуток [ -5; 5 ].
Постройте ее график, зная, что:
f ( x ) – четная .
б) f ( x ) – нечетная.

y = 2 x + 1
Существуют функции, которые не обладают свойствами чётности или нечётности.
График в этом случае не обладает свойством симметрии