признаков -Х2 или Х3 – нужно исключить из модели
Находят коэффициенты парной корреляции
Если их значения меньше 0,8, их включают в модель.
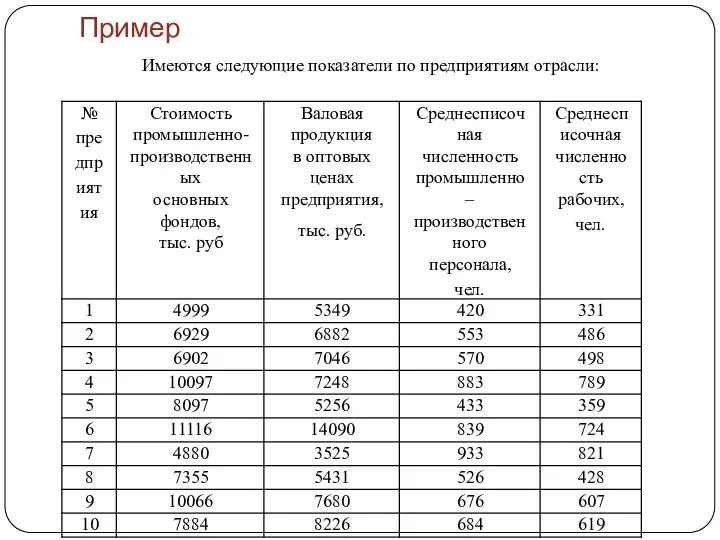
Рассчитать коэффициенты парной корреляции между каждым из факторов (в нашем примере Х2 и Х3)и результативным признаком Y:
Если, получилось, что , то исключают признак Х3
Если , то один из факторов можно исключить.
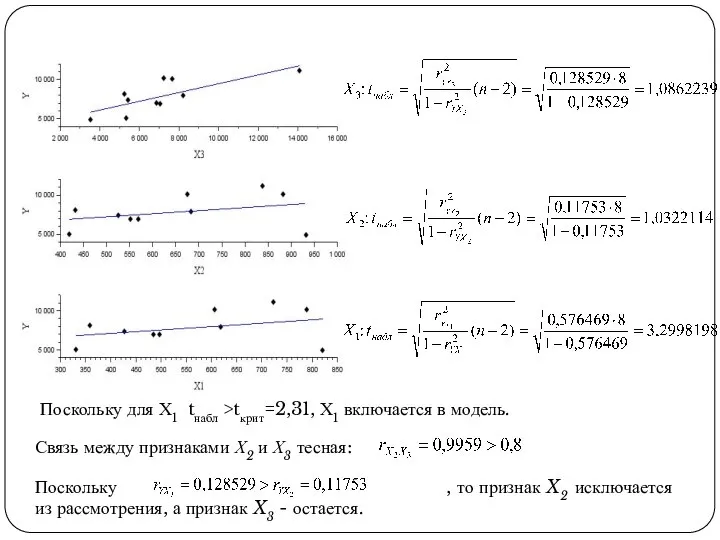
С помощью t-критерия Стьюдента:
Если tнабл>tкрит, (α ; n-2) то с вероятностью 1-α можно утверждать о значимости межфакторного коэффициента корреляции и, следовательно, о значимости факторного признака Xj. Он включается в модель.









 Упрощение логических операций
Упрощение логических операций Теорема Пифагора
Теорема Пифагора История системы мер длины (часть 2)
История системы мер длины (часть 2) Probability Distributions
Probability Distributions Биссектриса угла
Биссектриса угла Деление вида a:а, а:1
Деление вида a:а, а:1 Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов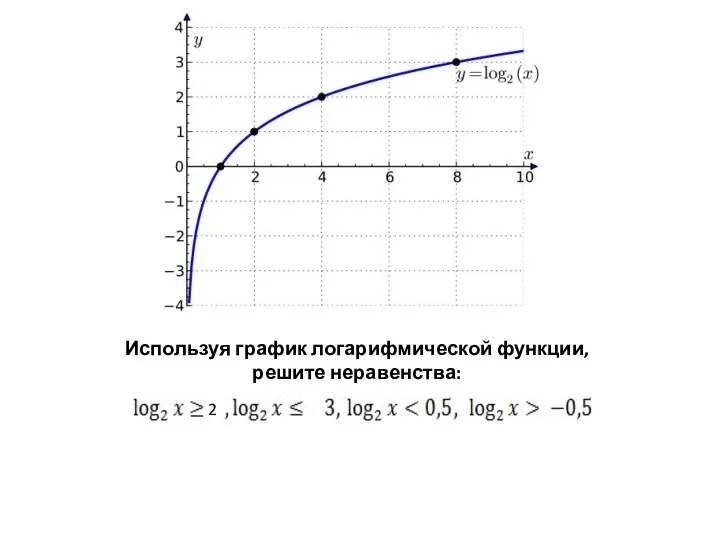 Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Матрица размера m x n
Матрица размера m x n Тренажер Состав числа
Тренажер Состав числа Отношения и золотое сечение
Отношения и золотое сечение Параллелограмм и его свойства и признаки
Параллелограмм и его свойства и признаки Страна Математика
Страна Математика Выполните вычисления и заполните таблицу. 6 класс
Выполните вычисления и заполните таблицу. 6 класс Матрицы и определители
Матрицы и определители Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Веселое путешествие
Веселое путешествие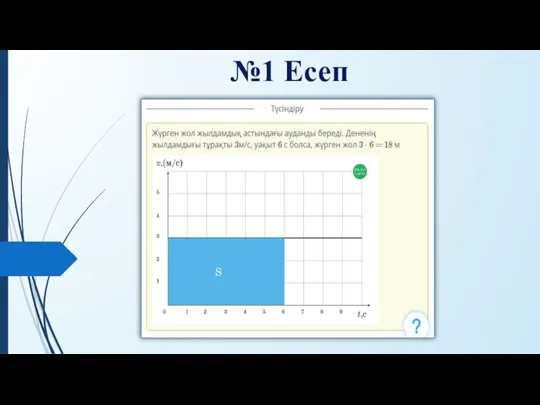 Есептер шығару
Есептер шығару Наши истинные учителя опыт и чувства. Из истории геометрии
Наши истинные учителя опыт и чувства. Из истории геометрии Параллельность прямых. Урок – практикум
Параллельность прямых. Урок – практикум Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами
Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами Проект по математике Задачи-расчеты из моей жизни
Проект по математике Задачи-расчеты из моей жизни Приближение вычисления
Приближение вычисления Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида Смешаное число
Смешаное число Состав числа (домики)
Состав числа (домики) Сопоставление эмпирических и теоретических частот
Сопоставление эмпирических и теоретических частот