- Главная
- Математика
- Динамическое программирование

Содержание
- 2. 2 Приложения динамического программирования В данном разделе рассмотрено четыре примера, каждый из которых выбран для демонстрации
- 3. 3
- 4. 4
- 5. 5
- 6. 6
- 7. 7 В таблице 5 сравниваются допустимые решения для каждого значения х3. Таблица 5 – Результаты этапа
- 8. 8
- 9. 9
- 10. 10 Задача замены оборудования Чем дольше механизм эксплуатируется, тем выше затраты на его обслуживание и ниже
- 11. 11
- 12. 12 Таблица 8 – Исходные данные к примеру 4 Определение допустимых значений возраста механизма на каждом
- 13. 13 Рисунок 3 – Схема возможной замены механизма
- 14. 14 Если однолетний механизм заменяется в начале второго или третьего года, то заменивший его механизм к
- 15. 15 Этап 3. Таблица 10 – Результаты этапа 3 задачи замена оборудования Этап 2. Таблица 11
- 16. 16 На рисунке 4 показана последовательность получения оптимального решения. В начале первого года оптимальным решением при
- 18. Скачать презентацию
Слайд 22
Приложения динамического программирования
В данном разделе рассмотрено четыре примера, каждый из которых
2
Приложения динамического программирования
В данном разделе рассмотрено четыре примера, каждый из которых

выбран для демонстрации методов динамического программирования. При рассмотрении каждого примера особое внимание обратите на три основных элемента моделей динамического программирования.
1. Определение этапов.
2. Определение на каждом этапе вариантов решения (альтернатив).
3. Определение состояний на каждом этапе.
Из перечисленных выше элементов понятие состояния, как правило, представляется весьма сложным для восприятия. Рассмотренные в этом разделе приложения последовательно показывают, что определение состояния меняется в зависимости от моделируемой ситуации. При рассмотрении каждого приложения полезно ответить на следующие вопросы:
1) какие соотношения связывают этапы вместе?
2) какая информация необходима для того, чтобы получить допустимые решения на текущем этапе без повторной проверки решений, принятых на предыдущих этапах?
1. Определение этапов.
2. Определение на каждом этапе вариантов решения (альтернатив).
3. Определение состояний на каждом этапе.
Из перечисленных выше элементов понятие состояния, как правило, представляется весьма сложным для восприятия. Рассмотренные в этом разделе приложения последовательно показывают, что определение состояния меняется в зависимости от моделируемой ситуации. При рассмотрении каждого приложения полезно ответить на следующие вопросы:
1) какие соотношения связывают этапы вместе?
2) какая информация необходима для того, чтобы получить допустимые решения на текущем этапе без повторной проверки решений, принятых на предыдущих этапах?
Слайд 77
В таблице 5 сравниваются допустимые решения для каждого значения х3.
Таблица 5 –
7
В таблице 5 сравниваются допустимые решения для каждого значения х3.
Таблица 5 –

Результаты этапа 3 задачи о загрузке
Этап 2. Таблица 6
(6)
Таблица 6 – Результаты этапа 2 задачи о загрузке
Этап 2. Таблица 6
(6)
Таблица 6 – Результаты этапа 2 задачи о загрузке
Слайд 1010
Задача замены оборудования
Чем дольше механизм эксплуатируется, тем выше затраты на его обслуживание
10
Задача замены оборудования
Чем дольше механизм эксплуатируется, тем выше затраты на его обслуживание

и ниже его производительность. Когда срок эксплуатации механизма достигает определенного уровня, может оказаться более выгодной его замена. Задача замены оборудования, таким образом, сводится к определению оптимального срока эксплуатации механизма.
Предположим, что мы занимаемся заменой механизмов на протяжении t лет. В начале каждого года принимается решение либо об эксплуатации механизма еще один год, либо о замене его новым. Обозначим через r(t) и c(t) прибыль от эксплуатации t-летнего механизма на протяжении года и затраты на его обслуживание за этот же период. Далее пусть s(t) - стоимость продажи механизма, который эксплуатировался t лет. Стоимость приобретения нового механизма остается неизменной на протяжении всех лет и равна I.
Элементы модели динамического программирования таковы.
1. Этап i представляется порядковым номером года, i = 1, 2, ..., n.
2. Вариантами решения на i-м этапе (т.е. для i-го года) являются альтернативы: продолжить эксплуатацию или заменить механизм в начале i-го года.
3. Состоянием на i-м этапе является срок эксплуатации t (возраст) механизма к началу i-го года.
Предположим, что мы занимаемся заменой механизмов на протяжении t лет. В начале каждого года принимается решение либо об эксплуатации механизма еще один год, либо о замене его новым. Обозначим через r(t) и c(t) прибыль от эксплуатации t-летнего механизма на протяжении года и затраты на его обслуживание за этот же период. Далее пусть s(t) - стоимость продажи механизма, который эксплуатировался t лет. Стоимость приобретения нового механизма остается неизменной на протяжении всех лет и равна I.
Элементы модели динамического программирования таковы.
1. Этап i представляется порядковым номером года, i = 1, 2, ..., n.
2. Вариантами решения на i-м этапе (т.е. для i-го года) являются альтернативы: продолжить эксплуатацию или заменить механизм в начале i-го года.
3. Состоянием на i-м этапе является срок эксплуатации t (возраст) механизма к началу i-го года.
Слайд 1111
11

Слайд 1212
Таблица 8 – Исходные данные к примеру 4
Определение допустимых значений возраста механизма
12
Таблица 8 – Исходные данные к примеру 4
Определение допустимых значений возраста механизма
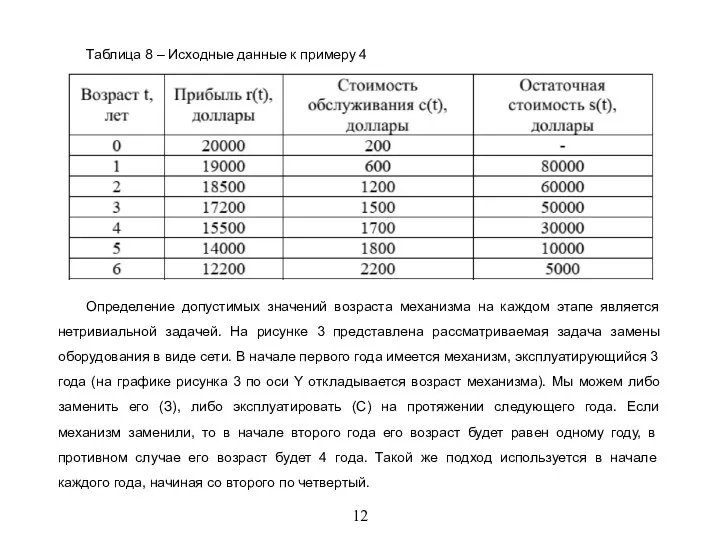
на каждом этапе является нетривиальной задачей. На рисунке 3 представлена рассматриваемая задача замены оборудования в виде сети. В начале первого года имеется механизм, эксплуатирующийся 3 года (на графике рисунка 3 по оси Y откладывается возраст механизма). Мы можем либо заменить его (З), либо эксплуатировать (С) на протяжении следующего года. Если механизм заменили, то в начале второго года его возраст будет равен одному году, в противном случае его возраст будет 4 года. Такой же подход используется в начале каждого года, начиная со второго по четвертый.
Слайд 1313
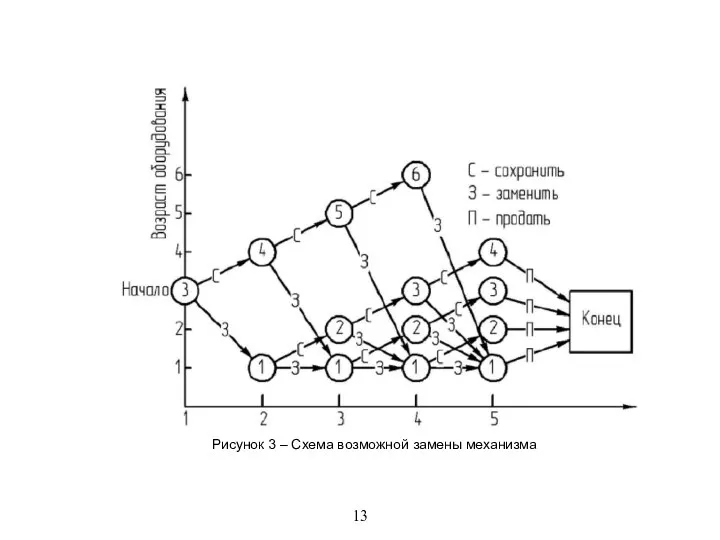
Рисунок 3 – Схема возможной замены механизма
13
Рисунок 3 – Схема возможной замены механизма
Слайд 1414
Если однолетний механизм заменяется в начале второго или третьего года, то заменивший
14
Если однолетний механизм заменяется в начале второго или третьего года, то заменивший

его механизм к началу следующего года также будет однолетним. К тому же, в начале 4-го года 6-летний механизм обязательно должен быть заменен, если он еще эксплуатируется; в конце 4-го года все механизмы продаются (П) в обязательном порядке. На схеме сети также видно, что в начале второго года возможны только механизмы со сроком эксплуатации 1 или 4 года. В начале третьего года механизм может иметь возраст 1, 2 или 5 лет, а в начале четвертого - 1, 2, 3 или 6 лет.
Решение данной задачи эквивалентно поиску маршрута максимальной длины (то есть приносящего максимальную прибыль) от начала первого года к концу четвертого в сети, показанной на рисунке 3. При решении этой задачи используем табличную форму записи (числовые данные в таблице кратны тысячам долларов).
Этап 4.
Таблица 9 – Результаты этапа 4 задачи замена оборудования
Решение данной задачи эквивалентно поиску маршрута максимальной длины (то есть приносящего максимальную прибыль) от начала первого года к концу четвертого в сети, показанной на рисунке 3. При решении этой задачи используем табличную форму записи (числовые данные в таблице кратны тысячам долларов).
Этап 4.
Таблица 9 – Результаты этапа 4 задачи замена оборудования
Слайд 1515
Этап 3.
Таблица 10 – Результаты этапа 3 задачи замена оборудования
Этап 2.
Таблица 11
15
Этап 3.
Таблица 10 – Результаты этапа 3 задачи замена оборудования
Этап 2.
Таблица 11

– Результаты этапа 3 задачи замена оборудования
Этап 1.
Таблица 12 – Результаты этапа 3 задачи замена оборудования
Этап 1.
Таблица 12 – Результаты этапа 3 задачи замена оборудования
Слайд 1616
На рисунке 4 показана последовательность получения оптимального решения. В начале первого года
16
На рисунке 4 показана последовательность получения оптимального решения. В начале первого года
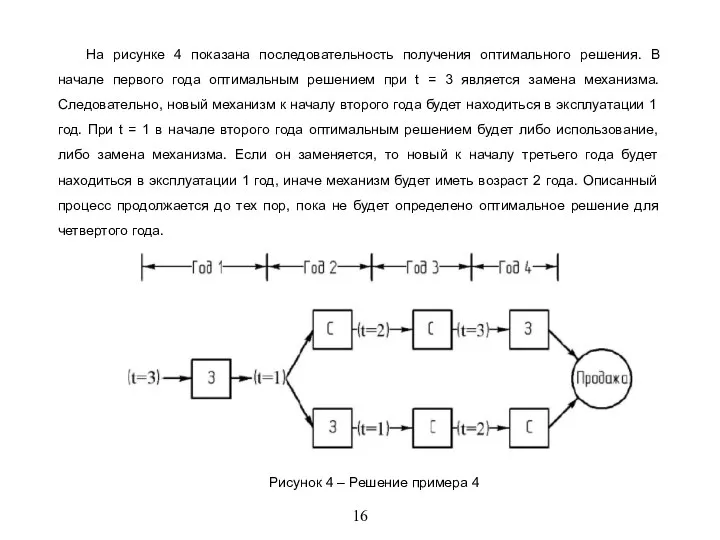
оптимальным решением при t = 3 является замена механизма. Следовательно, новый механизм к началу второго года будет находиться в эксплуатации 1 год. При t = 1 в начале второго года оптимальным решением будет либо использование, либо замена механизма. Если он заменяется, то новый к началу третьего года будет находиться в эксплуатации 1 год, иначе механизм будет иметь возраст 2 года. Описанный процесс продолжается до тех пор, пока не будет определено оптимальное решение для четвертого года.
Рисунок 4 – Решение примера 4
Рисунок 4 – Решение примера 4
- Предыдущая
ПсихообрразованиеСледующая -
Светоотражающие элементы





 Понятие интеграла
Понятие интеграла Решение комбинаторных задач
Решение комбинаторных задач Радианная мера угла. Поворот точки вокруг начала координат. Определение тригонометрических функций
Радианная мера угла. Поворот точки вокруг начала координат. Определение тригонометрических функций Проценты. 6 класс
Проценты. 6 класс Формула полной вероятности
Формула полной вероятности Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Приемы устных вычислений трехзначных чисел
Приемы устных вычислений трехзначных чисел Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ  L(q(x), h, H) шекаралық есептің меншікті мәндері және A(A) характеристикалық функцияның нөлдері
L(q(x), h, H) шекаралық есептің меншікті мәндері және A(A) характеристикалық функцияның нөлдері Преобразование дробей с помощью основного свойства
Преобразование дробей с помощью основного свойства Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы
Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы Проценты (5)
Проценты (5) Длиннее, короче. Одинаковые по длине
Длиннее, короче. Одинаковые по длине Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс Обработка экспериментальных данных. Описательная статистика: основные понятия
Обработка экспериментальных данных. Описательная статистика: основные понятия Занимательная геометрия
Занимательная геометрия Решение неравенств второй степени с одной переменной. Определение
Решение неравенств второй степени с одной переменной. Определение Параллельность прямой и плоскости
Параллельность прямой и плоскости Методы решения тригонометрических уравнений. 10 класс
Методы решения тригонометрических уравнений. 10 класс Найдите лишнюю фигуру и объясните свой выбор
Найдите лишнюю фигуру и объясните свой выбор Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями Нахождение угла между двумя прямыми в пространстве
Нахождение угла между двумя прямыми в пространстве Предмет и методы теории систем. Лекция 1
Предмет и методы теории систем. Лекция 1 ерпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах
ерпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах Площадь поверхности цилиндра
Площадь поверхности цилиндра Интерактивная игра-тренажер по математике
Интерактивная игра-тренажер по математике Кривые линии. Комплексный чертеж поверхности
Кривые линии. Комплексный чертеж поверхности