Содержание
- 2. Методы минимизации функций многих переменных
- 3. Методы безусловной минимизации функций многих переменных Поверхностью уровня функции f(x) называется множество точек, в которых функция
- 4. Функция f(x) называется дифференцируемой в точке , если существует такой вектор , что для любого x
- 5. Если f(x) дифференцируема, то направлением наибыстрей- шего убывания функции f(x) в точке является направ- ление антиградиента
- 6. Матрицей Гессе H(x) дважды непрерывно дифференцируемой в точке x функции f(x) называется матрица частных производных второго
- 7. Определение
- 9. Методы безусловной минимизации функций многих переменных Метод покоординатного спуска ( конфигураций или Хука-Дживса) Метод конфигураций включает
- 10. Метод покоординатного спуска Основная идея метода покоординатного спуска
- 11. Метод покоординатного спуска
- 12. Метод покоординатного спуска
- 13. Алгоритм метода покоординатного спуска
- 14. Геометрическая интерпретация
- 15. ПРИМЕР
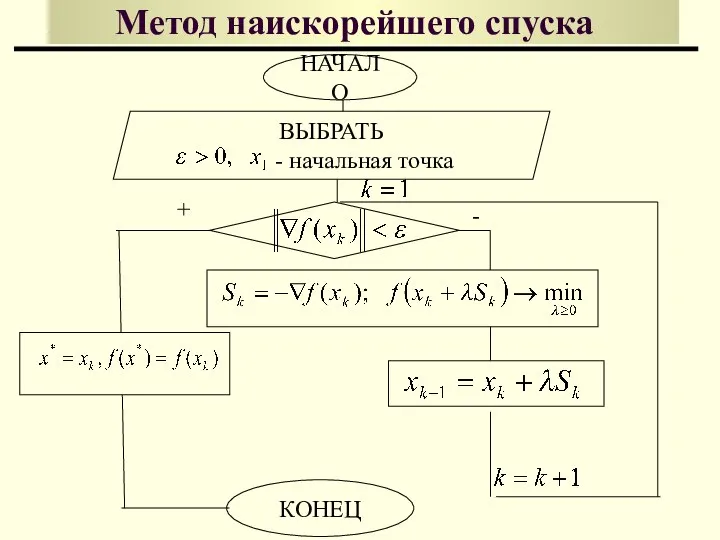
- 17. Метод наискорейшего спуска Идея метода наискорейшего спуска Геометрическая интерпретация
- 18. ВЫБРАТЬ - начальная точка Метод наискорейшего спуска НАЧАЛО КОНЕЦ + -
- 20. Метод наискорейшего спуска Замечания: Метод наискорейшего спуска сходится достаточно быстро, если для минимизирующей функции поверхности уровня
- 21. ПРИМЕР
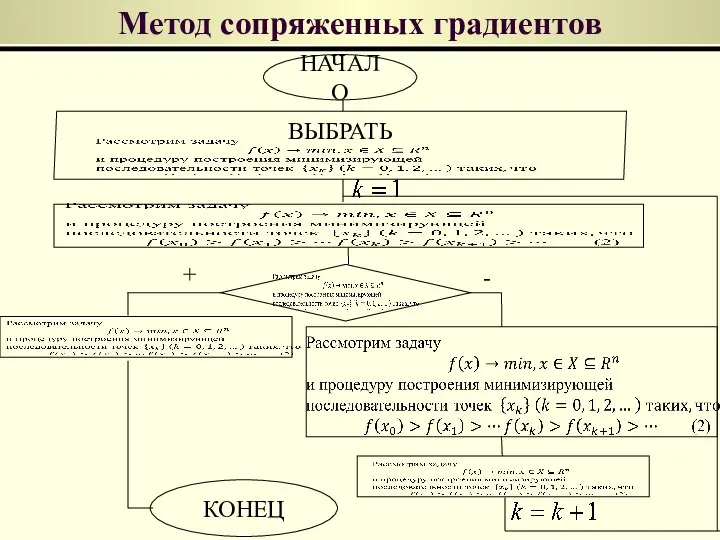
- 22. Метод сопряженных градиентов Геометрическая интерпретация Иллюстрация последовательных приближений метода наискорейшего спуска и метода сопряжённых градиентов к
- 23. Обоснование метода сопряженных градиентов Определение Нулевая итерация
- 25. Метод сопряженных градиентов ВЫБРАТЬ НАЧАЛО КОНЕЦ + -
- 26. Замечание: Если требуется найти глобальный минимум функции f(x), То для строго выпуклой f(x) Решение этой задачи
- 27. ПРИМЕР
- 28. Метод Ньютона Метод Ньютона относится к градиентным методам второго порядка, в котором направление минимизации выбирается умножением
- 29. Метод Ньютона
- 31. Алгоритм метода Ньютона
- 32. Алгоритм метода Ньютона
- 33. ПРИМЕР
- 35. Скачать презентацию






























 Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость
Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость Соотношение величин
Соотношение величин Методы обработки данных и способы их представления в научном исследовании
Методы обработки данных и способы их представления в научном исследовании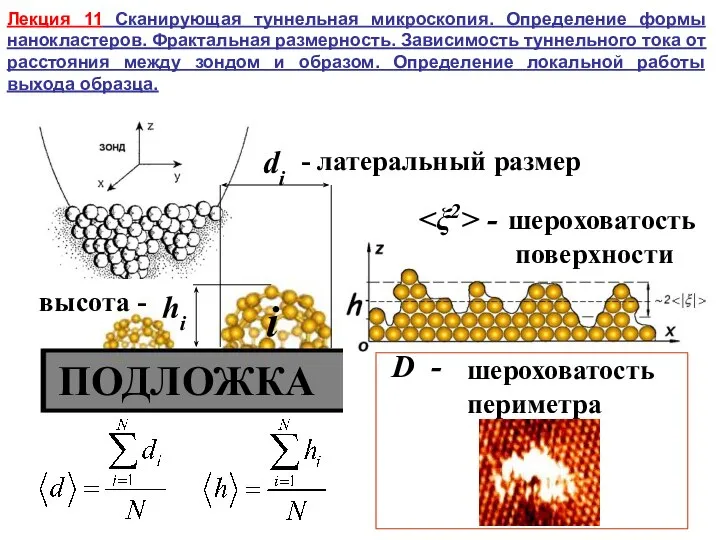 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Начальные сведения о задачах оптимизации
Начальные сведения о задачах оптимизации Юный математик
Юный математик Параллельные и перпендикулярные прямые
Параллельные и перпендикулярные прямые Первообразная. 11 класс
Первообразная. 11 класс Экстремум. Условный экстремум функции 2 переменных
Экстремум. Условный экстремум функции 2 переменных Кривые второго порядка
Кривые второго порядка Теорема Пифагора. Урок геометрии в 8 классе
Теорема Пифагора. Урок геометрии в 8 классе Презентация на тему Приёмы быстрого счета
Презентация на тему Приёмы быстрого счета  Презентация на тему Равнобедренный треугольник, признаки равенства треугольников
Презентация на тему Равнобедренный треугольник, признаки равенства треугольников  Разложение на множители с помощью формул
Разложение на множители с помощью формул Проектная деятельность на уроках математики. Задания для групповой работы (1-2 класс)
Проектная деятельность на уроках математики. Задания для групповой работы (1-2 класс) Неопределённый интеграл
Неопределённый интеграл Задачи на умножение
Задачи на умножение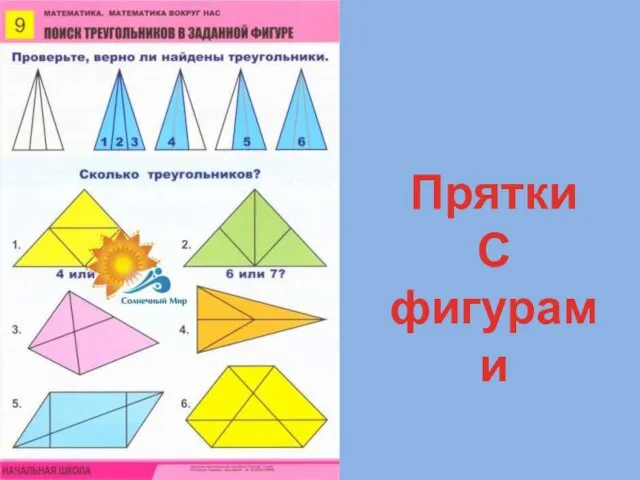 Прятки с фигурами
Прятки с фигурами Построение сечений
Построение сечений Основы матричной алгебры
Основы матричной алгебры Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Деление и степень числа. Тест
Деление и степень числа. Тест Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования
Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования Закономерности между элементами фигуры и тенью при освещении параллельными лучами
Закономерности между элементами фигуры и тенью при освещении параллельными лучами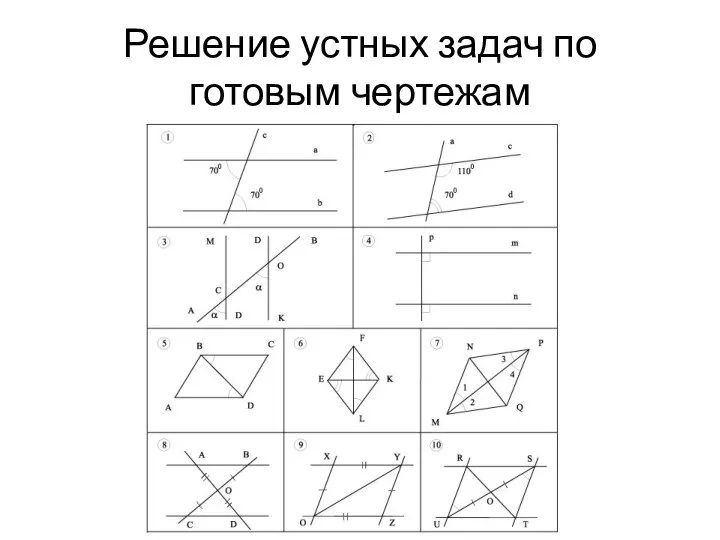 Решение устных задач по готовым чертежам
Решение устных задач по готовым чертежам Элементы высшей математики. Свойства операции умножения
Элементы высшей математики. Свойства операции умножения Окружность и круг
Окружность и круг