Содержание
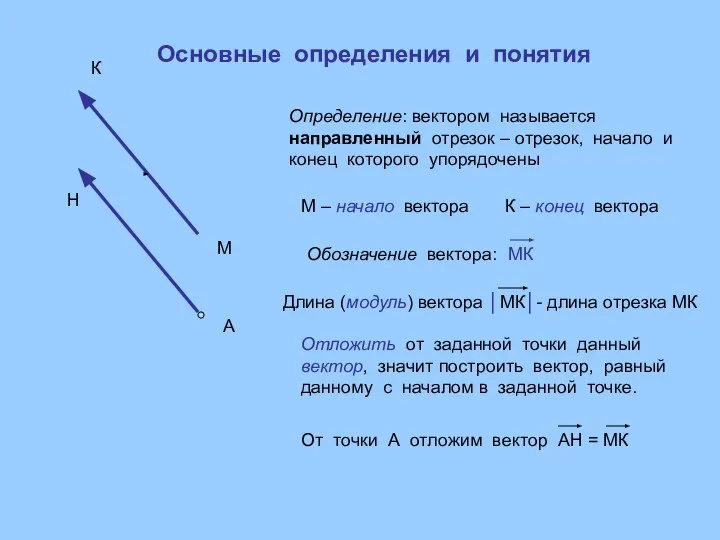
- 2. Определение: вектором называется направленный отрезок – отрезок, начало и конец которого упорядочены М К М –
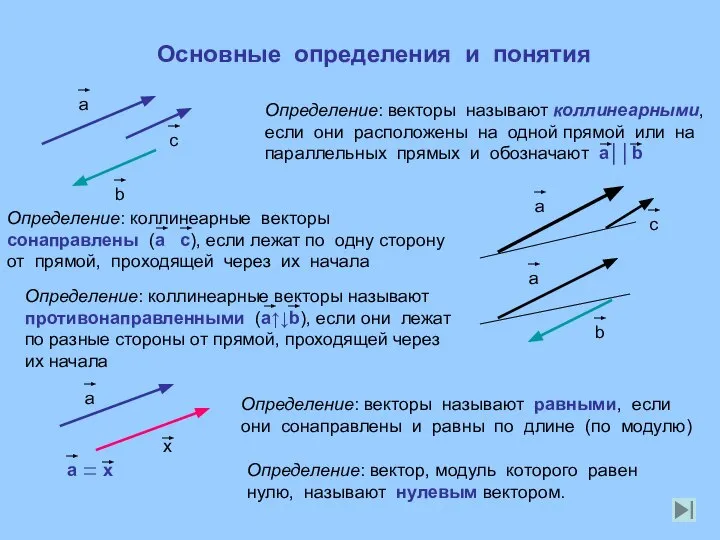
- 3. Основные определения и понятия Определение: векторы называют равными, если они сонаправлены и равны по длине (по
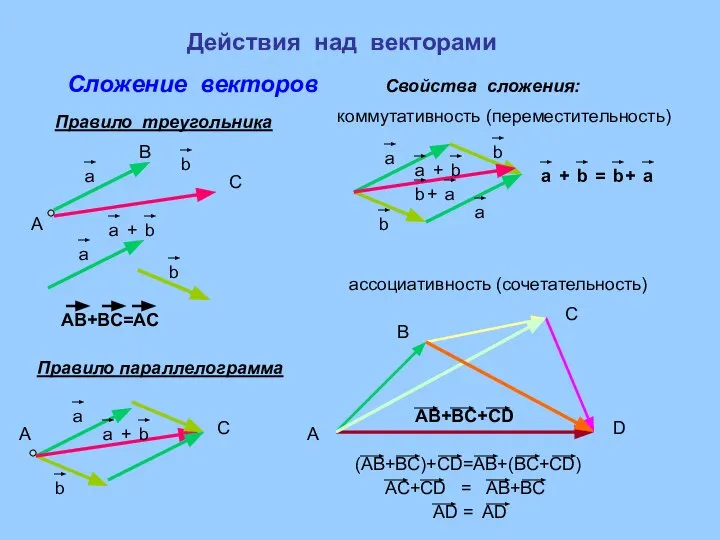
- 4. Действия над векторами Сложение векторов Правило треугольника А В С Правило параллелограмма А Свойства сложения: С
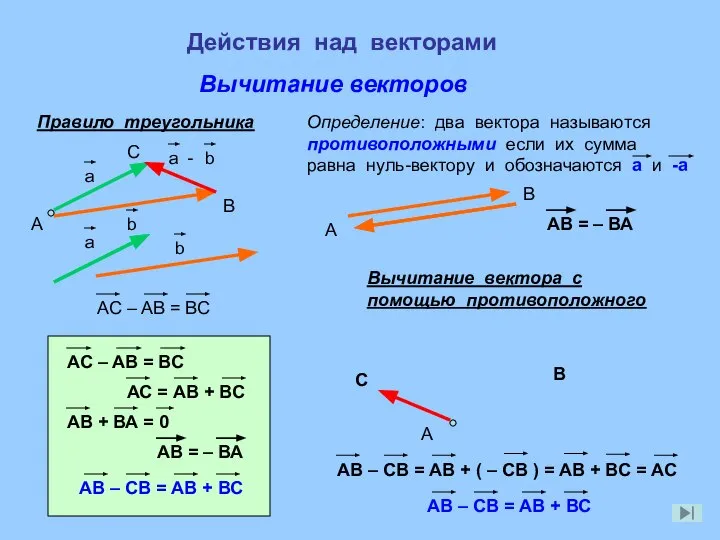
- 5. Действия над векторами Вычитание векторов А Правило треугольника B C Вычитание вектора с помощью противоположного А
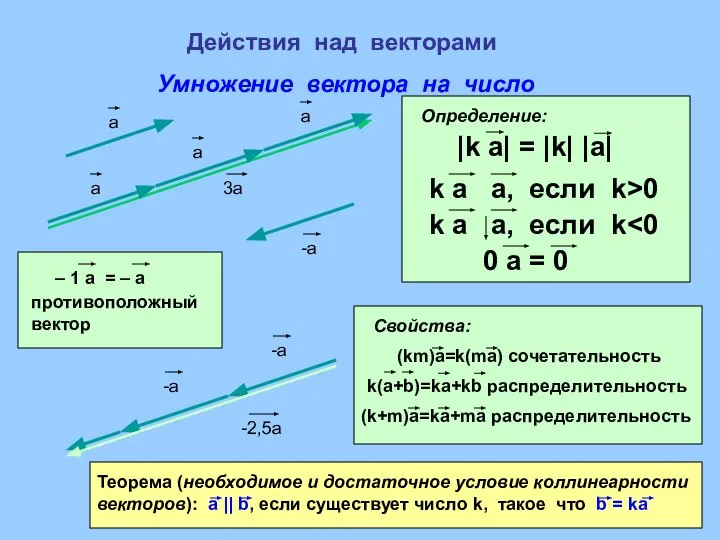
- 6. Действия над векторами Умножение вектора на число Определение: Свойства:
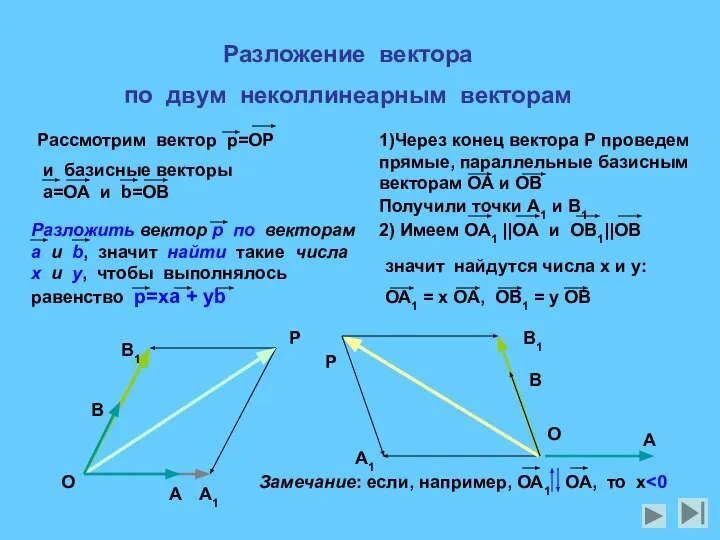
- 7. Разложение вектора по двум неколлинеарным векторам А1 В1 Получили точки А1 и В1
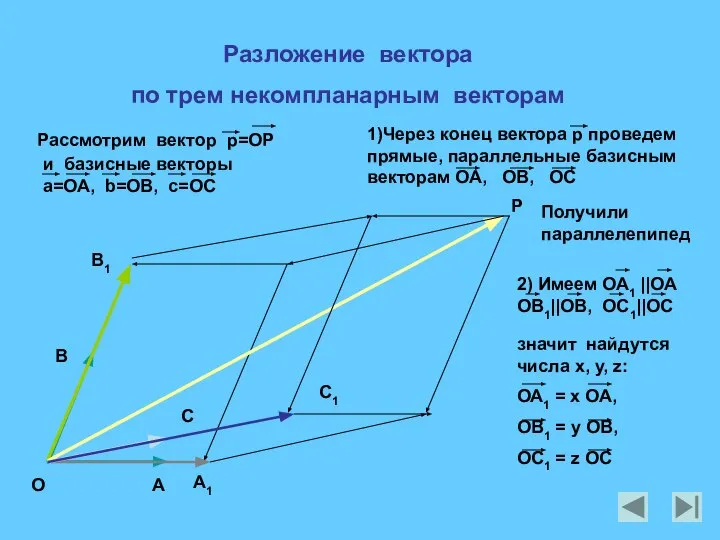
- 8. Разложение вектора по трем некомпланарным векторам Получили параллелепипед
- 9. Действия над векторами Скалярное умножение векторов Определение: скалярным произведением векторов а и b называется произведение длин
- 11. Скачать презентацию

 Определение и свойства тройных интегралов
Определение и свойства тройных интегралов Логарифмы вокруг нас
Логарифмы вокруг нас Монотонность, экстремумы
Монотонность, экстремумы Функции и графики
Функции и графики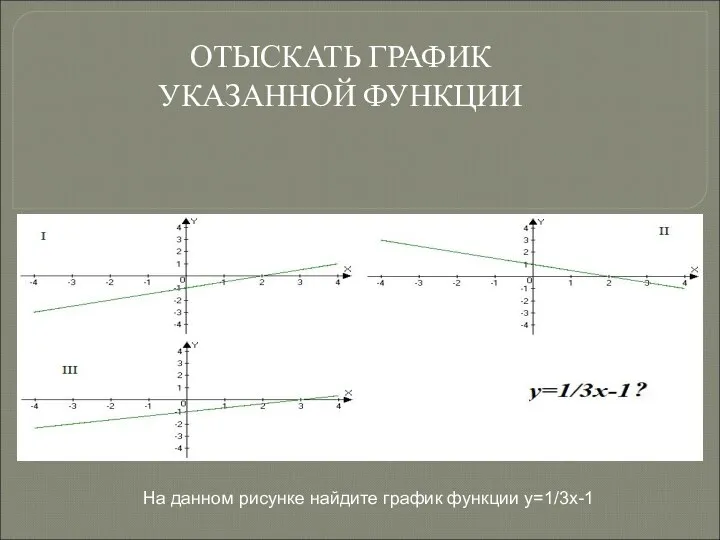 Виды графиков линейной функции
Виды графиков линейной функции Числа, кратные 2
Числа, кратные 2 Числа по порялку
Числа по порялку Решение неравенств
Решение неравенств Мир многогранников
Мир многогранников Разминка. Линейная функция
Разминка. Линейная функция Таблицы по алгебре
Таблицы по алгебре Вычисление площадей и объемов. Лекция №5
Вычисление площадей и объемов. Лекция №5 Неопределенный интеграл
Неопределенный интеграл Современные технологии статистического учета
Современные технологии статистического учета Интерактивный тренажёр В стране Математики. 1 класс
Интерактивный тренажёр В стране Математики. 1 класс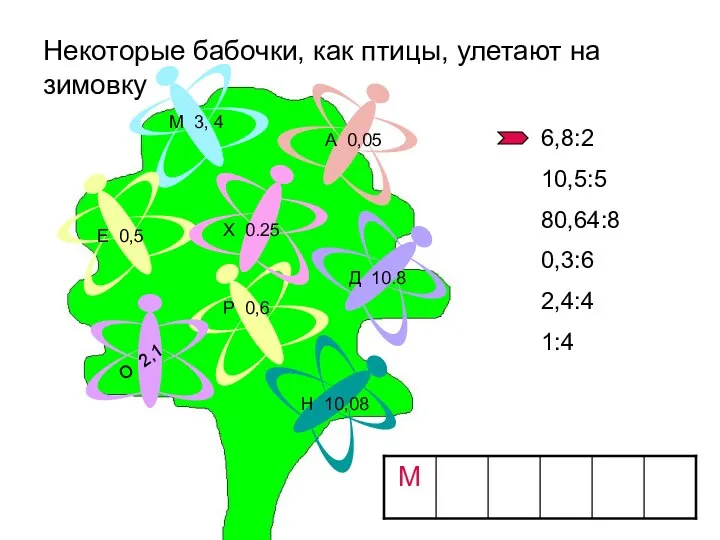 Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку
Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку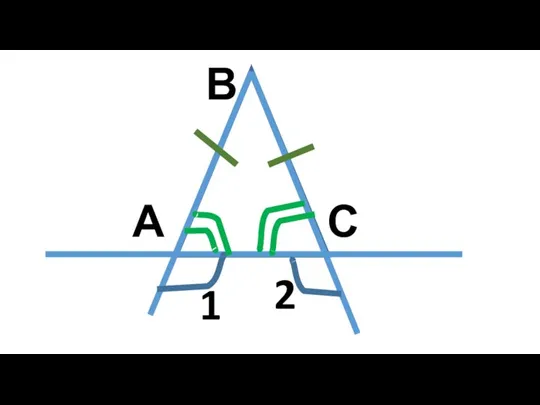 Равнобедренный треугольник
Равнобедренный треугольник Графические диктанты для детей. Рисуем по клеточкам
Графические диктанты для детей. Рисуем по клеточкам Область определения выражения
Область определения выражения Графы. Пути с таблицами
Графы. Пути с таблицами Параллельные прямые, перпендикулярные к плоскости
Параллельные прямые, перпендикулярные к плоскости Умножение многочлена на многочлен
Умножение многочлена на многочлен Разбор Мат.Вертикали. 6 класс
Разбор Мат.Вертикали. 6 класс Перпендикуляр и наклонная к плоскости
Перпендикуляр и наклонная к плоскости Определение свойств функции по графику
Определение свойств функции по графику Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества
Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества Решение простейших тригонометрических уравнений с помощью числовой окружности
Решение простейших тригонометрических уравнений с помощью числовой окружности Умножение на двузначное число
Умножение на двузначное число