Элементы комбинаторики

Это раздел математики, в котором исследуется, сколько различных комбинаций (всевозможных объединений элементов), подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству.
02.11.2020
Комбинаторика

Задачи, требующие перебора различных вариантов решения или поиска их числа называются комбинаторными
Сколькими способами можно выбрать…
Направо пойдешь, - коня потеряешь
Налево пойдешь, - голову сложишь, прямо
пойдешь…
02.11.2020

Если два действия взаимно исключают друг друга, и одно из них можно выполнить K способами, а другое P способами, то оба действия можно выполнить K +P числом способов.
Правило сложения
Чтобы использовать закон сложения:
1. Нужно понять, каковы группы, из которых нужно выбрать 1 элемент;
2. Нужно выяснить количество элементов в каждой группе;
3. Нужно убедиться, что в различных группах, из которых выбирают элемент, нет одинаковых элементов.
02.11.2020

Яна решила выбрать обед в столовой колледжа. Так как у нее немного денег, то она может выбрать только одно блюдо.
В меню столовой 3 вида холодных закусок, 7 вариантов первых блюд и 9 вариантов вторых. Сколькими способами она может выбрать ОДНО БЛЮДО?
Задача на применение закона сложения
02.11.2020

1. Каковы группы?
- 3 группы: холодные закуски, первые и вторые блюда
2. Сколько элементов в группах?
Закуску можно выбрать 3 способами;
Первое блюдо выбрать 7 способами;
Второе блюдо можно выбрать 9 способами.
3. Убедимся, что в группах нет одинаковых элементов.
4. Применим закон сложения: 3+7+9=19
Ответ: Одно блюдо можно выбрать 19 способами.
Решение
02.11.2020

Если одну часть действия можно выполнить K способами, а другую -P способами, то все действие можно выполнить K.P числом способов
Правило произведения
Закон умножения используется, чтобы вычислить число упорядоченных комбинаций - размещений
02.11.2020

Лена и Артем зашли в кафе.
На витрине лежит 25 вариантов десертов.
Ребята из них выбирают 2 десерта.
Выясните, сколькими различными способами может выбрать 2 десерта?
Задача на применение правила произведения
02.11.2020

1. Сначала ребята могут выбрать любой из всех 25 десертов.
2. Когда первый выбор сделан, для следующего остаётся 25−1=24 вариантов выбора десерта.
3. По закону умножения:
Если элемент A можно выбрать k способами и затем второй элемент B можно выбрать m различными способами, пару элементов A и B можно выбрать k⋅m способами.
1-й десерт выбирают 25 способами
2 -й десерт выбираем 24 способами
Используем правило произведения
2 десерта выбираем 25⋅24=600 (способами).
Ответ
Ребята могут выбрать десерт 600 различными способами.
Решение
02.11.2020

В задачах по комбинаторике часто встречается понятие факториала.
n! («эн факториал») – это произведение всех натуральных чисел от 1 до n включительно:
n!=n*(n-1)*(n-2)…3*2*1
Например: 5!=5*4*3*2*1=120
4!=4*3*2*1=24, то есть 5!=5*4!
0!=1
Факториал
02.11.2020

Расположение различных n элементов в определенном порядке называется перестановкой без повторений из n элементов.
Pn=n!
Перестановки — это специальный случай размещений, когда выборка так же велика, как данное множество.
Важно! В заданиях на перестановки, не важно назвать сами перестановки, а важно назвать их число.
Перестановки ( без повторений)
02.11.2020

Хор колледжа для Рождественского концерта приготовил 4 народных песен. В концертной программе один раз нужно проиграть каждую песню. Сколько можно составить концертных программ, если порядок песен важен?
Задача на перестановки
02.11.2020

Решение
02.11.2020

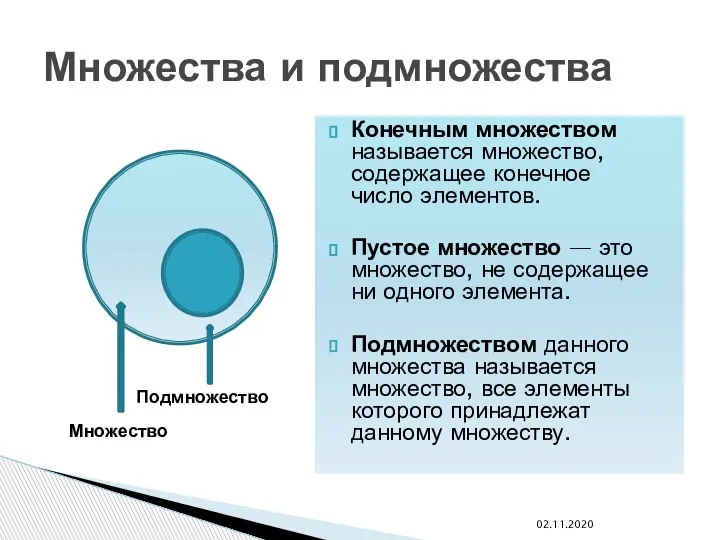
Конечным множеством называется множество, содержащее конечное число элементов.
Пустое множество — это множество, не содержащее ни одного элемента.
Подмножеством данного множества называется множество, все элементы которого принадлежат данному множеству.
Множества и подмножества
02.11.2020

Выборками называются подмножества какого-либо множества.
Упорядоченными выборками называются выборки, в которых важен порядок элементов.
Если в выборке поменяют местами два элемента и получится другая выборка, то данная выборка является упорядоченной.
Неупорядоченными выборками называются выборки, в которых не важен порядок элементов.
Выборки
02.11.2020

Неупорядоченные выборки:
Из 10 претендентов на место повара в кафе нужно выбрать 2 поваров. (Меняя местами поваров, пара останется той же.
Гена из 8 книг выбирает для чтения 3 книги.(Меняя местами книги, не изменится выбранная литература.)
Пример
Упорядоченные выборки:
Из 10 претендентов для работы в кафе нужно выбрать шеф-повара и повара по приготовлению холодных блюд.
Меняя местами 2 претендентов, изменятся их должности.
Гена из 8 книг выбирает для чтения 3 книги и составляет список их прочтения.
Меняя книги местами, получится другой список.
02.11.2020

Комбинации, в которых имеет значение порядок элементов, называются размещениями.
В размещениях у каждого элемента своя определённая роль.
Размещения — это упорядоченные наборы
Например: пара учеников — староста класса и его помощник; пара цифр — десятки и единицы.
Размещения
(порядок имеет значение)
02.11.2020

n-показывает количество элементов данного множества
m показывает количество элементов размещения (сколько элементов выбирается)
Размещения без повторения
Читается: А из n по m
02.11.2020

Для прохождения практики студентов есть14 столовых.
Вычислите, сколькими способами можно устроить трёх человек, чтобы они были в разных столовых?
Задача на применение формулы размещения
02.11.2020

Требуемая выборка — размещение, т.к. порядок элементов важен.
Например, если первый человек будет работать в столовой A,
второй — в столовой B, а третий — в столовой C,
Меняя местами людей, получатся новые ситуации — новые выборки.
Нужно вычислить, сколькими способами можно выбрать k элементов из n элементов, где n=14; k=3 Применяем формулу:
Решение
02.11.2020

Сочетанием из n элементов по m элементов (m≤n) называется выборка элементов m из данного неупорядоченного множества.
Отличие сочетаний от размещений:
В размещениях порядок выборки важен
В сочетаниях порядок выборки не важен
Сочетания
02.11.2020

На полке лежит 10 различных книг по кулинарии. Сколькими различными способами можно выбрать три книги для написания реферата ?
Задача на сочетания
02.11.2020

Решение
Требуемая выборка — сочетания.
Нужно вычислить, сколькими способами можно выбрать k элементов из n элементов, если порядок неважен.
02.11.2020

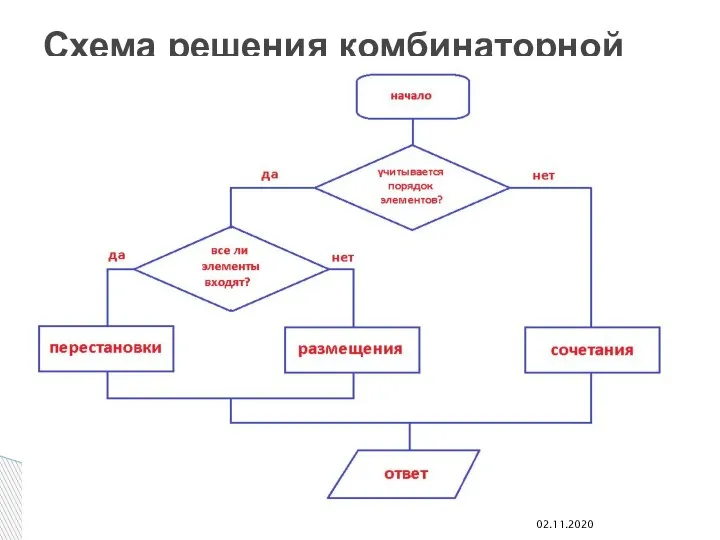
Схема решения комбинаторной задачи
02.11.2020