Содержание
- 3. Решение системы уравнений.
- 5. Перестановка уравнений Вычеркивание из системы нулевых уравнений Умножение обеих частей одного из уравнений системы на число,
- 6. Метод Гаусса – метод последовательного исключения переменных
- 7. Метод Гаусса
- 8. Продолжая процесс последовательного исключения переменных, получим систему уравнений, в которой для каждого уравнения имеется неизвестное, которое
- 9. Если для каждого уравнения зафиксировано такое неизвестное, то это неизвестное называется базисным, а весь набор базисных
- 10. Пример 1. Решить систему уравнений
- 11. В результате преобразований Гаусса получим таблицу:
- 13. Однородные системы линейных уравнений
- 14. Однородная система всегда совместна: одно из её решений – нулевое. Теорема. Однородная система, в которой число
- 15. Пример 2. Найти общее решение системы уравнений.
- 16. Решим систему методом Гаусса
- 17. Перейдем к записи системы уравнений
- 19. Действия над векторами
- 20. Действия над векторами
- 21. Определение.
- 22. Системы векторов в линейном пространстве
- 23. Определение
- 24. Пример
- 25. Определения.
- 26. Линейная независимость векторов.
- 27. Пример.
- 28. Решение.
- 29. Базис линейного пространства
- 30. Пример.
- 31. Основные утверждения.
- 32. Примеры.
- 33. Ранг и базис системы векторов.
- 34. Пример.
- 35. Евклидовы пространства.
- 38. Ортогональные системы векторов
- 40. Скачать презентацию





































 Проверка математических данных в произведении Н. Носова Незнайка на Луне
Проверка математических данных в произведении Н. Носова Незнайка на Луне Площадь. Фигуры
Площадь. Фигуры Задание 19. Профиль (1)
Задание 19. Профиль (1) Упрощение выражений. Тест
Упрощение выражений. Тест Формулы сложения
Формулы сложения Движение по окружности
Движение по окружности Вавилонская математика
Вавилонская математика ЛекцияЭлементы комбинаторики
ЛекцияЭлементы комбинаторики Прямая и обратная пропорциональность
Прямая и обратная пропорциональность Презентация4. МСиТИ
Презентация4. МСиТИ Уравнение касательной к графику функции
Уравнение касательной к графику функции Первые уроки в 5 кассе
Первые уроки в 5 кассе Задачи на проценты
Задачи на проценты Числовые равенства и их свойства
Числовые равенства и их свойства Площадь ромба
Площадь ромба Сочетания. 9 класс
Сочетания. 9 класс Двугранный угол
Двугранный угол Золотое сечение. 9 класс
Золотое сечение. 9 класс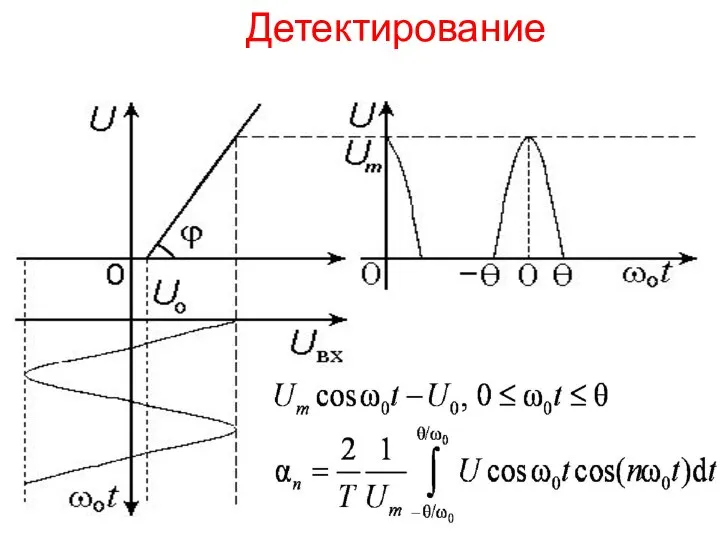 Детектирование. Функции и коэффициенты Берга
Детектирование. Функции и коэффициенты Берга Математическая игра-раскраска Обезьянка
Математическая игра-раскраска Обезьянка Структура арифметической задачи
Структура арифметической задачи Графический диктант Раскрытие скобок
Графический диктант Раскрытие скобок Эконометрика. Оценка влияния количественных показателей друг на друга
Эконометрика. Оценка влияния количественных показателей друг на друга Презентация на тему Формулы суммы и разности синуса и косинуса
Презентация на тему Формулы суммы и разности синуса и косинуса  Перпендикулярность прямых, прямой и плоскости
Перпендикулярность прямых, прямой и плоскости Корреляционный анализ. Тема 9
Корреляционный анализ. Тема 9 Упражнения по планиметрии на готовых чертежах. VII класс
Упражнения по планиметрии на готовых чертежах. VII класс Определение длины остряков и тяговых усилий для их перевода
Определение длины остряков и тяговых усилий для их перевода