Содержание
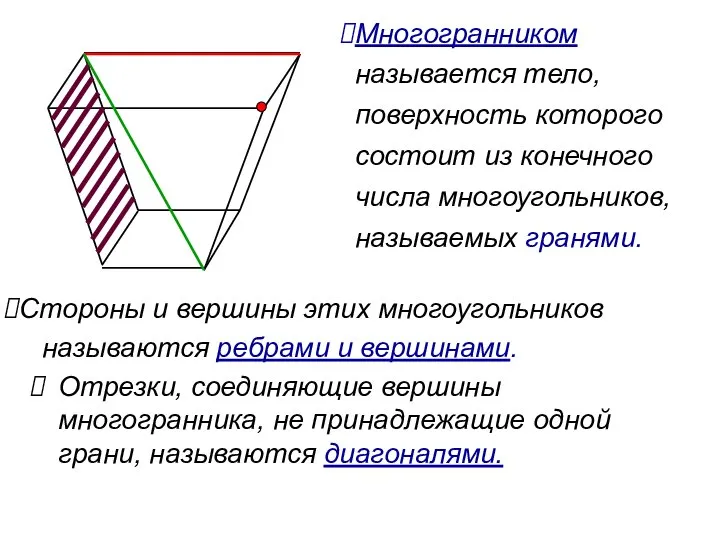
- 2. Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями. Многогранником называется тело, поверхность которого состоит
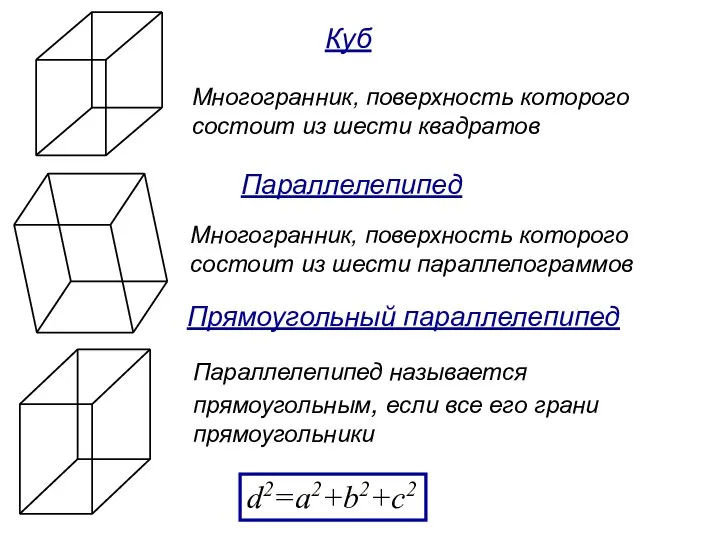
- 3. Многогранник, поверхность которого состоит из шести квадратов Многогранник, поверхность которого состоит из шести параллелограммов Параллелепипед называется
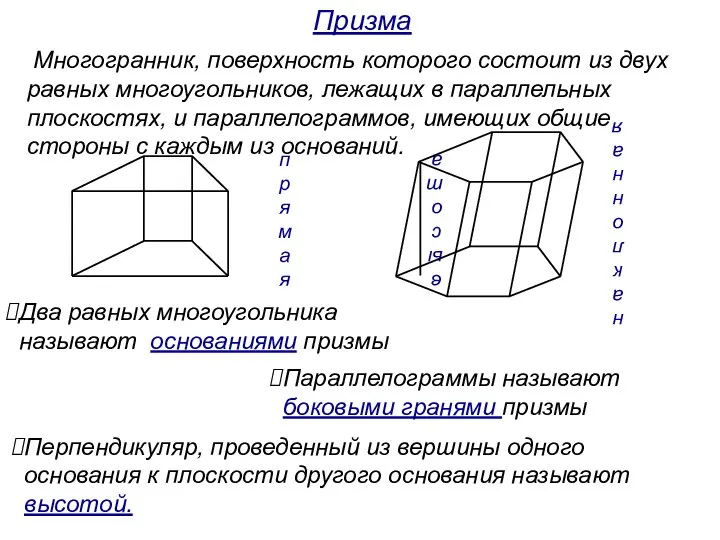
- 4. Многогранник, поверхность которого состоит из двух равных многоугольников, лежащих в параллельных плоскостях, и параллелограммов, имеющих общие
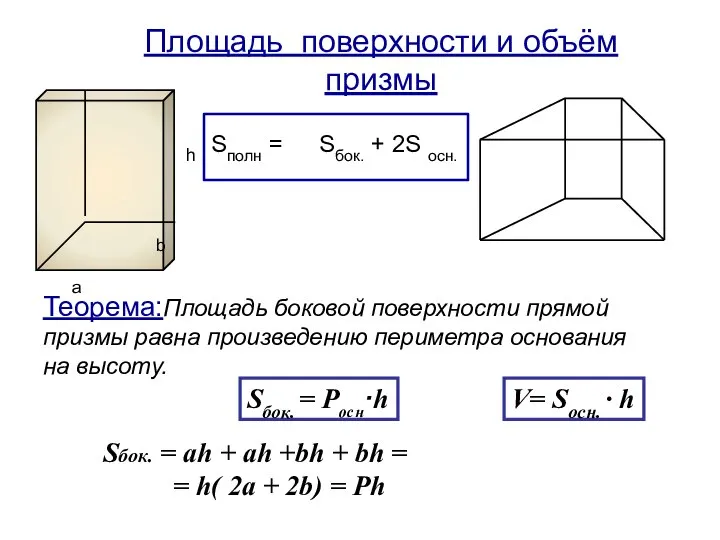
- 6. Площадь поверхности и объём призмы Sбок. + 2S осн. Sбок. = Pосн·h a b h Теорема:Площадь
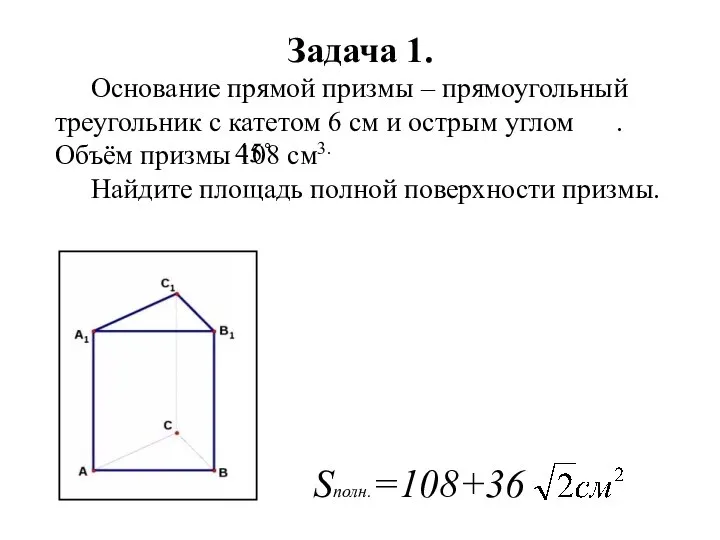
- 7. Задача 1. Основание прямой призмы – прямоугольный треугольник с катетом 6 см и острым углом .
- 8. Задача 4. Найти площадь поверхности и объём прямой призмы, основанием которой является ромб со стороной 6
- 10. Скачать презентацию

 Случаи вычитания 15-
Случаи вычитания 15- Применение свойств квадратичной функции при решении задач
Применение свойств квадратичной функции при решении задач Булевы выражения. Глава 2
Булевы выражения. Глава 2 Решение задач
Решение задач Показательная функция
Показательная функция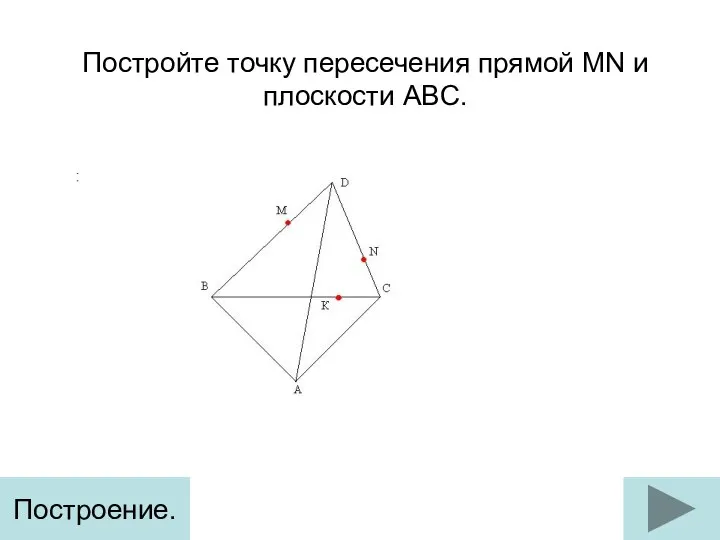 Точка пересечения прямой MN и плоскости ABC. Построение (задание 1)
Точка пересечения прямой MN и плоскости ABC. Построение (задание 1) Составные уравнения
Составные уравнения Теорема Пифагора. Урок 27
Теорема Пифагора. Урок 27 Тела вращения в природе
Тела вращения в природе Число есть слово неизречённое
Число есть слово неизречённое Подготовка к ВПР
Подготовка к ВПР Иррациональные уравнения и их системы. Иррациональные неравенства
Иррациональные уравнения и их системы. Иррациональные неравенства lecture5
lecture5 Prezentatsia_Microsoft_PowerPoint(1)
Prezentatsia_Microsoft_PowerPoint(1) Несобственные интегралы второго рода
Несобственные интегралы второго рода Свойства умножения и деления
Свойства умножения и деления История одной задачи
История одной задачи Proizvodnaya_funktsii
Proizvodnaya_funktsii Векторы на плоскости и в пространстве
Векторы на плоскости и в пространстве Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции
Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции Сочетания и размещения. 11 класс
Сочетания и размещения. 11 класс Презентация на тему Равнобедренная трапеция
Презентация на тему Равнобедренная трапеция  Решение логарифмических уравнений
Решение логарифмических уравнений Способы задания функции
Способы задания функции Сечение
Сечение Длина ломанной
Длина ломанной Векторы в пространстве
Векторы в пространстве Диференціальні рівняння
Диференціальні рівняння