Эмпирико-статистические модели климатических изменений. Земля как климатическая система

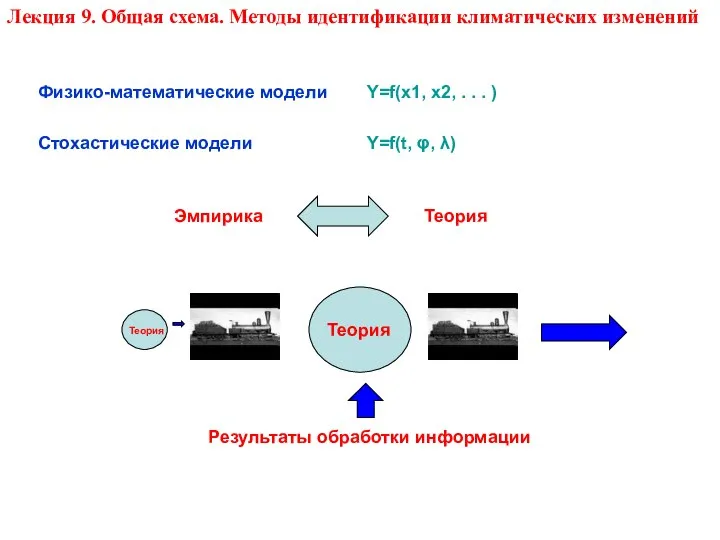
Теория
Эмпирика
Физико-математические модели
Стохастические модели
Y=f(t, φ, λ)
Y=f(x1, x2, . . . )
Результаты обработки информации
Теория
Теория
Лекция 9. Общая схема. Методы идентификации климатических изменений

Методология стационарной модели
Основные положения:
однородная выборка,
стационарность основных параметров (среднее и дисперсия), случайное событие = характеристике за каждый год,
все свойства цикличности отображаются, как правило, одним параметром (коэффициент автокорреляции между смежными членами ряда)
Краеугольные камни концепции однородной – стационарной выборки
с автокорреляцией
МОДЕЛЬ:
- простая цепь Маркова (время) ,
- однородное распределение с 2-3 параметрами (коллектив)

Методология динамической модели
- неоднородная выборка,
возможна нестационарность параметров,
случайное событие необязательно 1 раз в год (погодичное),
цикличность представляется напрямую в виде параметров циклов
Краеугольные камни концепции неоднородной – нестационарной выборки
МОДЕЛЬ:
- Сумма циклических составляющих разного временного масштаба;
- Композиция распределений стационарных компонент + сумма нестационарных компонент

В. Характеристики циклов многолетних колебаний:
T – период цикла;
A – амплитуда цикла,
Tup – продолжительность подъема,
Td - продолжительность спада,
Vup – скорость подъема,
Vd - скорость спада,
W - объем цикла.
Случайные события
А. Отдельные события
р.Бурея - Каменка
Б. Внутригодовые обобщения:
- среднегодовые,
среднемесячные,
выборочные в году экстремумы (максимумы и минимумы),
параметры внутригодовой функции

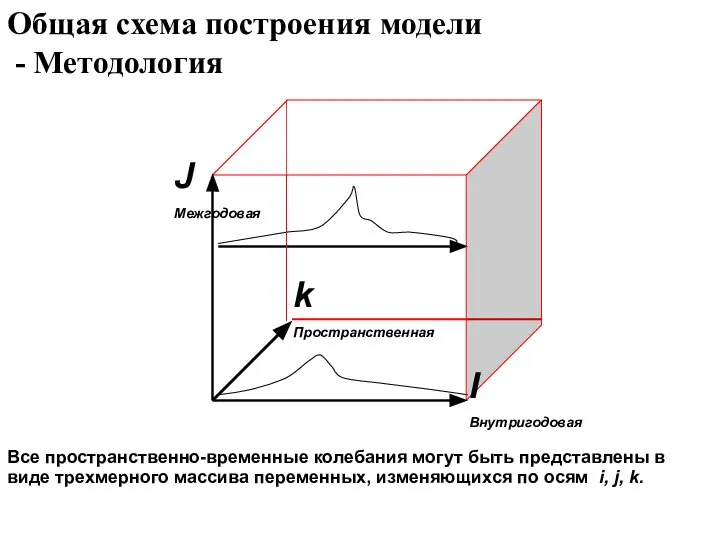
Общая схема построения модели
- Методология
Все пространственно-временные колебания могут быть представлены в
виде трехмерного массива переменных, изменяющихся по осям i, j, k.

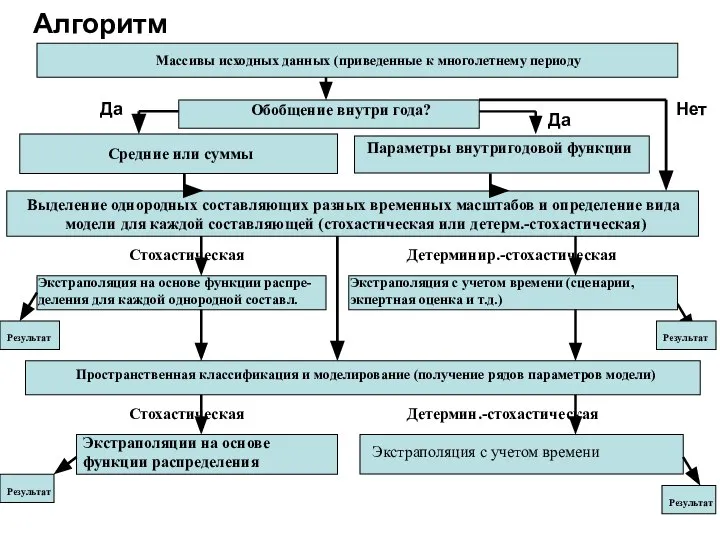
Алгоритм
Стохастическая
Детермин.-стохастическая

S(Ch) ≤ Δy - динамическая,
Δy < S(Ch) ≤ 100 - Δy - динамико-стохастическая,
S(Ch) > 100 - Δy - стохастическая,
где: S(Ch) - стандарт остаточной дисперсии зависимости
рассматриваемой характеристики (Ch) от времени (t):
Ch = ƒ(t);
Δy - относительная погрешность гидрометеорологической
характеристики (в %).
Вид модели временного ряда

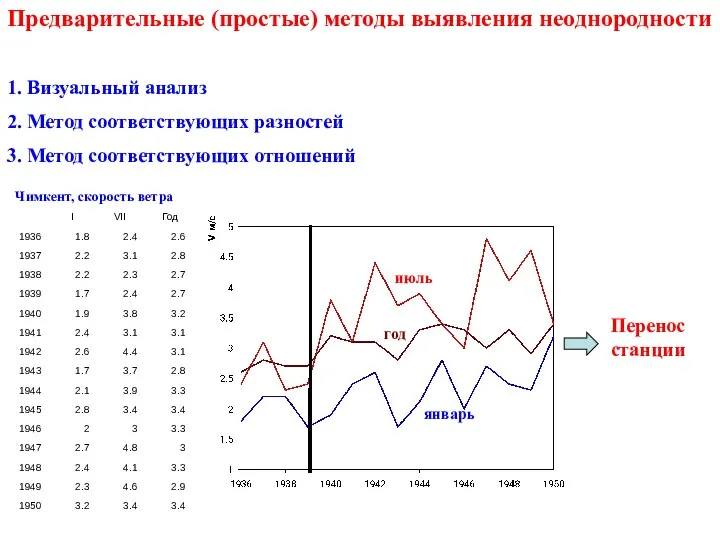
Предварительные (простые) методы выявления неоднородности
1. Визуальный анализ
2. Метод соответствующих разностей
3. Метод соответствующих отношений
Чимкент, скорость ветра
январь
июль
год
Перенос
станции

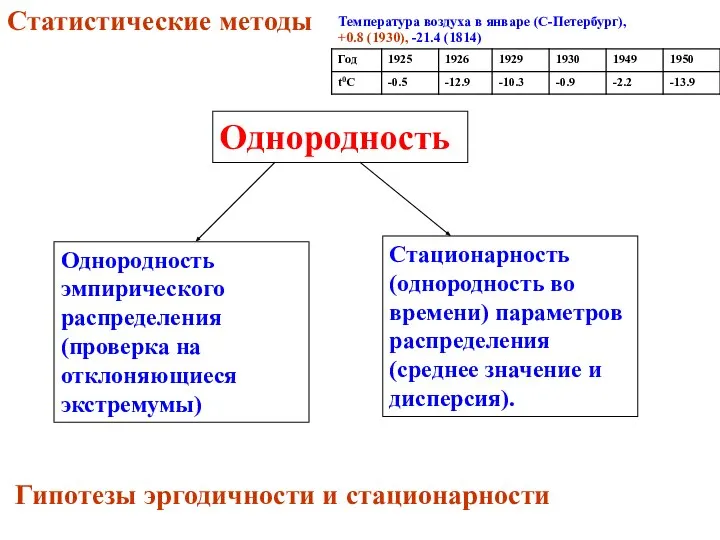
Однородность
Однородность эмпирического распределения (проверка на отклоняющиеся экстремумы)
Стационарность (однородность во времени) параметров распределения
(среднее значение и дисперсия).
Статистические методы
Гипотезы эргодичности и стационарности
Температура воздуха в январе (С-Петербург),
+0.8 (1930), -21.4 (1814)

F=σ2j / σ2j+1
при σ2j >σ2j+1. где σ2j. σ2j+1 – соответственно дисперсии двух следующих друг за другом подвыборок (j и j+1) объемом n1 и n2
Методы оценки стационарности параметров временных рядов
Критерий Фишера для дисперсий:
Критерий Стьюдента для средних:
где: g – коэффициент, учитывающий влияние асимметрии
исходной совокупности и определяемый по табл.
r – коэффициент автокорреляции между смежными членами
ряда.
где: YcpI. YcpII. σ2I. σ2II – средние значения и дисперсии двух последовательных выборок. n1 и n2 - объемы выборок.
t'б=Ct · tб
где: t'б – критическое значение статистики Стьюдента при наличии автокорреляции,
tб – критическое значение статистики Стьюдента для случайной совокупности при том же числе степеней свободы k= n1+ n2-2;
Ct – переходный коэффициент, определяемый в зависимости от коэффициента автокорреляции

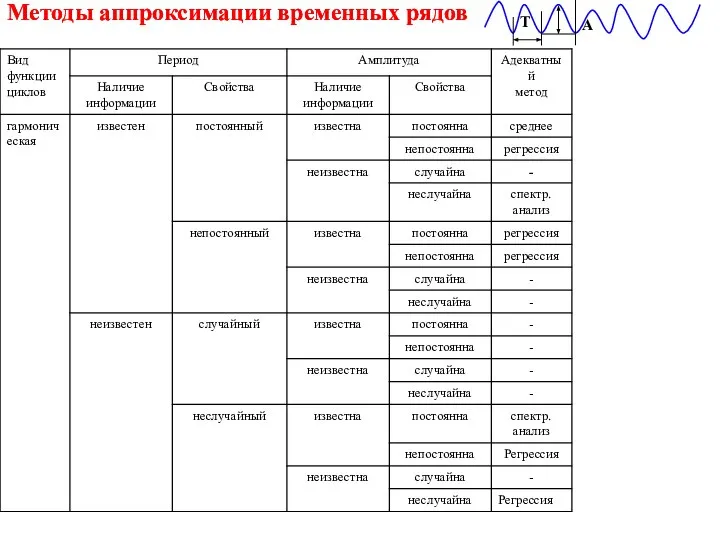
Методы аппроксимации временных рядов
Методы аппроксимации временных рядов
T

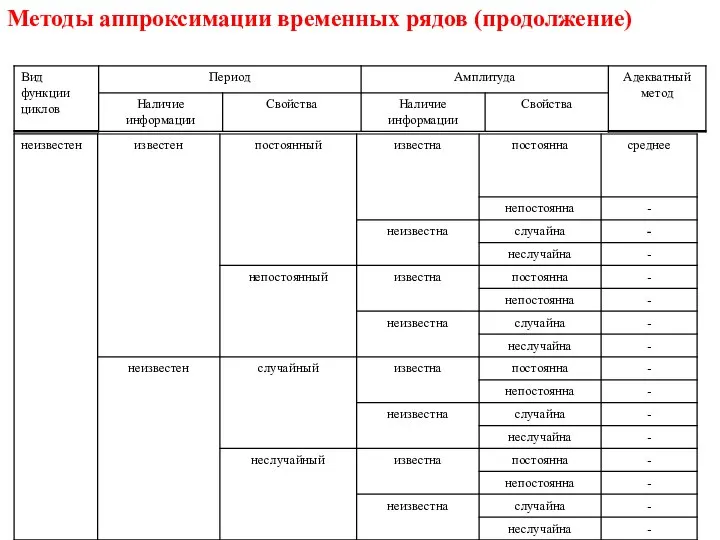
Методы аппроксимации временных рядов (продолжение)

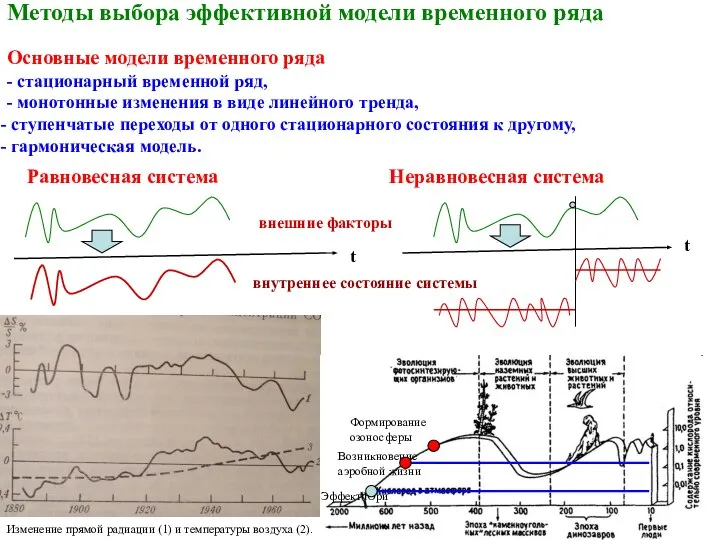
Методы выбора эффективной модели временного ряда
- стационарный временной ряд,
- монотонные изменения в виде линейного тренда,
ступенчатые переходы от одного стационарного состояния к другому,
гармоническая модель.
Основные модели временного ряда
Равновесная система
внешние факторы
внутреннее состояние системы
Изменение прямой радиации (1) и температуры воздуха (2).
Неравновесная система
t
t
Возникновение аэробной жизни
Эффект Юри
Формирование озоносферы

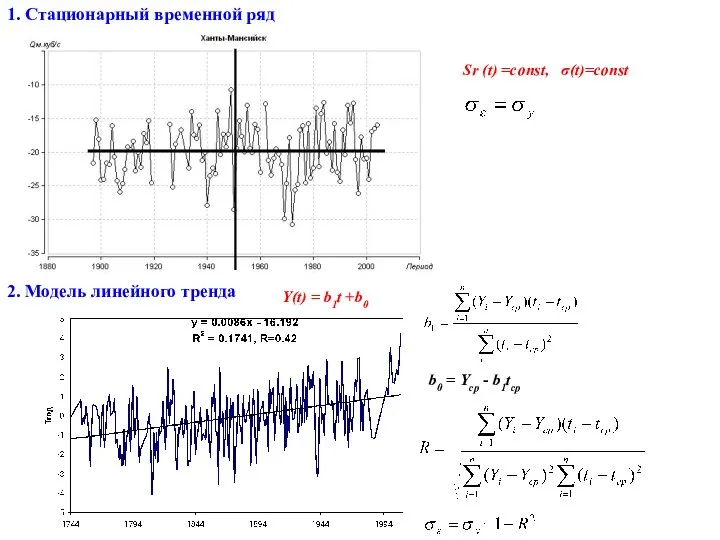
1. Стационарный временной ряд
Sr (t) =const, σ(t)=const
2. Модель линейного тренда
Y(t) = b1t +b0
b0 = Ycp - b1tcp

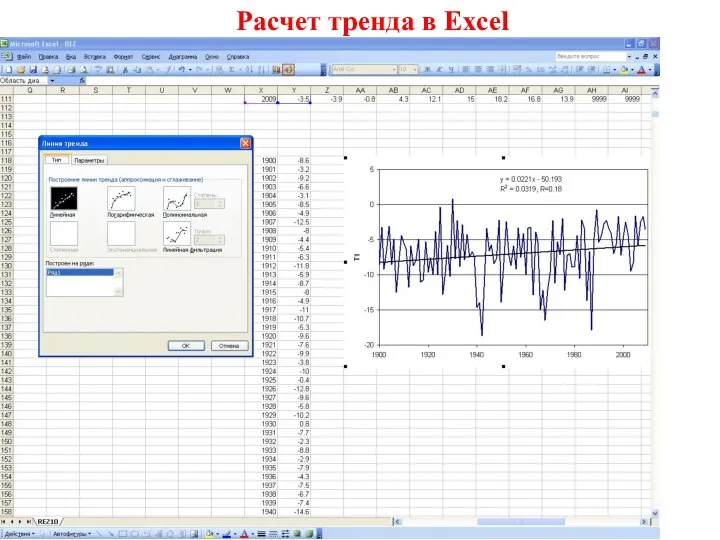
Расчет тренда в Excel

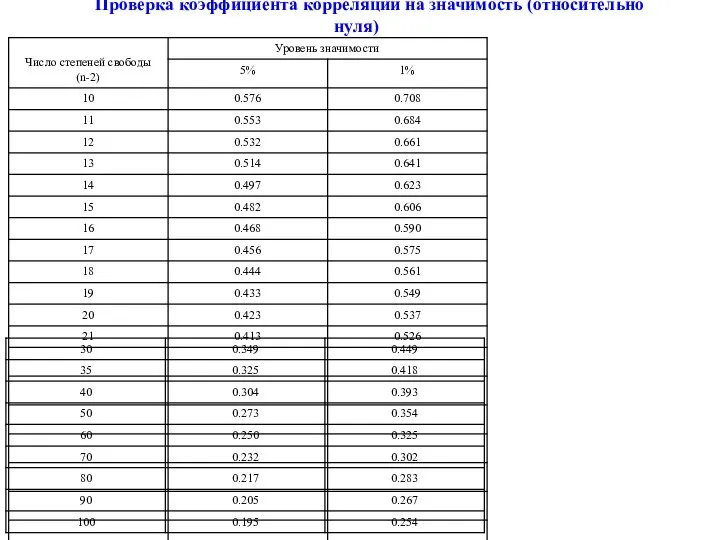
Таблица 1.
Проверка коэффициента корреляции на значимость (относительно нуля)
Проверка коэффициента корреляции на значимость (относительно нуля)

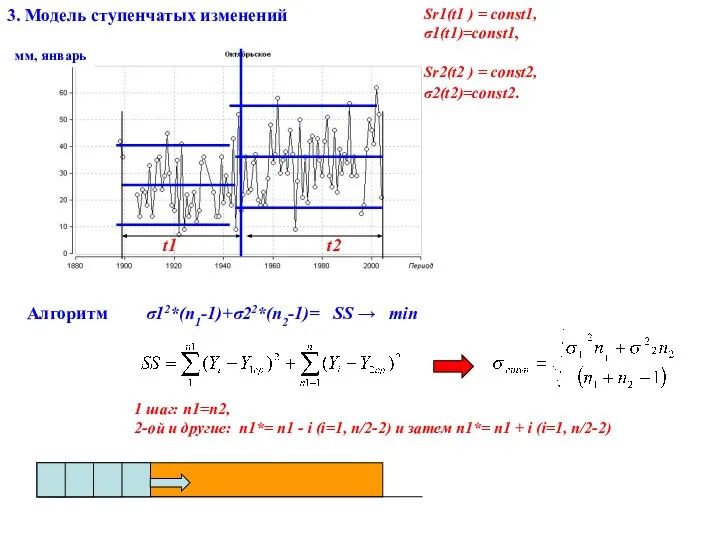
3. Модель ступенчатых изменений
мм, январь
Sr1(t1 ) = const1, σ1(t1)=const1,
Sr2(t2 ) = const2, σ2(t2)=const2.
t1
t2
σ12*(n1-1)+σ22*(n2-1)= SS → min
Алгоритм
1 шаг: n1=n2,
2-ой и другие: n1*= n1 - i (i=1, n/2-2) и затем n1*= n1 + i (i=1, n/2-2)

4. Гармоническая модель
B1 = (∑ (Yi - Ycp )(Xi - Xcp ))/(∑(Xi - Xcp )2
B0 = Ycp - B1Xcp
Xi=sin(ti/T1)
Статистическая значимость коэффициента B1
B1 /σB1≥ Bкр
σB1 - стандартная случайная погрешность коэффициента B1
для j=1
B1 -2σB1 ≤ B1 ≤ B1+2σB1
для j=2

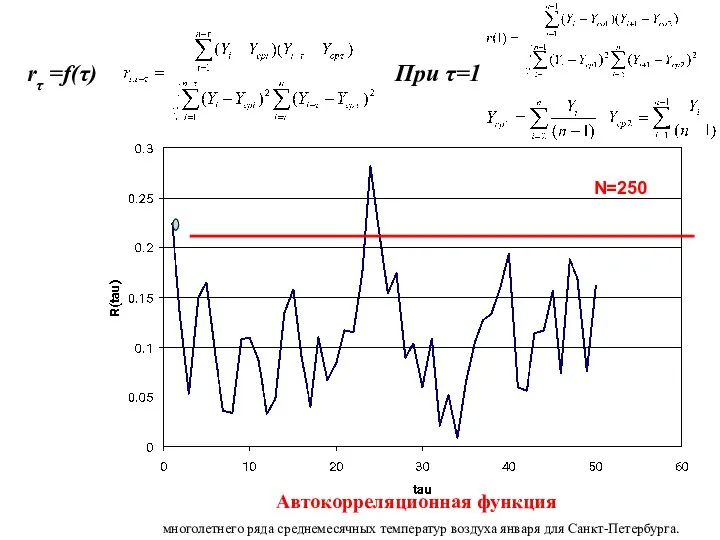
Автокорреляционная функция
N=250
rτ =f(τ)
При τ=1
многолетнего ряда среднемесячных температур воздуха января для Санкт-Петербурга.

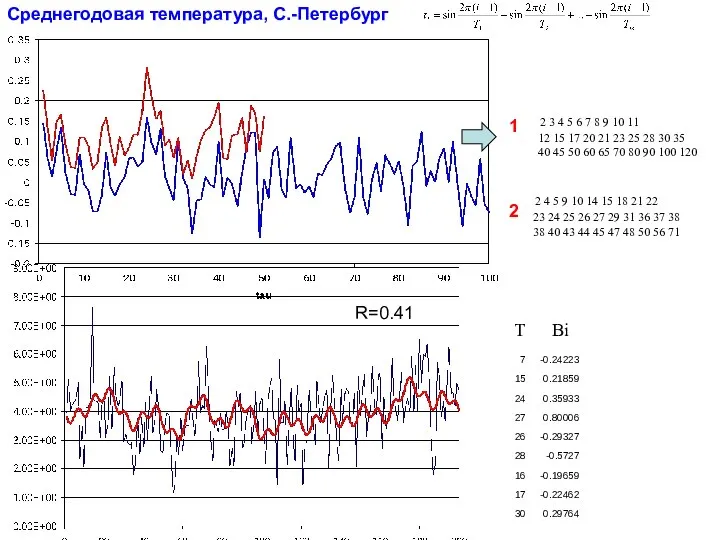
Среднегодовая температура, С.-Петербург
2 3 4 5 6 7 8 9 10 11
12 15 17 20 21 23 25 28 30 35
40 45 50 60 65 70 80 90 100 120
2 4 5 9 10 14 15 18 21 22
23 24 25 26 27 29 31 36 37 38
38 40 43 44 45 47 48 50 56 71
1
2
T Bi
R=0.41

Относительные погрешности по отношению к стационарной модели

Последовательность выполнения работы
1. Выбрать временной ряд климатической характеристики: многолетний ряд среднемесячная температура воздуха или сумм осадков за месяц.
2. Удлинить временной ряд и заполнить пропуски наблюдений по ряду в пункте-аналоге.
3. Построить график временного ряда в редакторе Excel.
4. Рассчитать основные параметры временного ряда: среднее значение (Yср ), дисперсия (σ2Y), среднее квадратическое отклонение (σy), коэффициент автокорреляции между смежными членами ряда (r(1)).
5. Определить коэффициенты модели линейного тренда (2): коэффициенты уравнения регрессии b1, и b0 , коэффициент корреляции R, стандартное отклонение (σε) и дисперсию остатков (σ2ε). Для расчетов можно воспользоваться редактором Excel.
6. Представить модель линейного тренда на графике временного ряда в редукторе Excel.
7. Разбить график временного ряда на две части дате наиболее вероятного ступенчатого изменения. Для каждой из двух частей рассчитать основные параметры выборки: среднее значение, дисперсию, среднее квадратическоне отклонение.
8. Рассчитать стандартное отклонение остатков относительно модели ступенчатых изменений (σступ) по формуле (21).
9. Представить модель ступенчатых изменений на графике временного ряда в редакторе Excel.
10. Рассчитать коэффициенты автокорреляции временного ряда при τ от 1 до 30 по формуле (19) или средствами редактора Excel.
11. Построить график автокорреляционной функции временного ряда (rτ =f(τ)) , в редакторе Excel и на нем выбрать 1-2 наибольших значения.
12. Оценить статистическую значимость коэффициентов автокорреляции, определив критическое значение коэффициента автокорреляции r*(1) по табл.1.
13. Осуществить функциональные преобразования вида Xi=sin(ti/T1) и определить коэффициенты уравнения (8) B1, B2 и B0, коэффициент множественной корреляции R уравнения (8), стандарт остатков (σгар) и остаточную дисперсию уравнения (σ2гар). Для расчетов параметров уравнения с двумя факторами можно применять редактор Excel и е вычислительные статистические пакеты (“Статистика” и другие).
14. Представить модель гармонических колебаний на графике временного ряда в редакторе Excel.
15. Рассчитать относительные погрешности моделей тренда, ступенчатых изменений и гармоник по отношению к стационарной модели по формулам (22) –(24).
16. Рассчитать статистики критерия Фишера по формулам (25) – (27) и сравнить их с критическими значениями при уровне значимости 5% (табл. Критических статистик Фишера из лаб. работы №1).
17. Результаты расчетов пп.15 и 16 представить в таблице

Результаты лабораторной работы должны быть представлены в файле Word, включающем:
1) таблицу с многолетним рядом (рядами) анализируемой климатической характеристики;
2) многолетний график ряда наблюдений;
3) многолетний график и его аппроксимация моделью линейного тренда;
4) многолетний график и его аппроксимация моделью ступенчатых изменений;
5) график автокорреляционной функции;
6) многолетний график и его аппроксимация гармонической моделью;
7) таблицы с параметрами моделей линейного тренда, ступенчатых изменений и гармонических колебаний, включающая: коэффициенты уравнений, коэффициенты корреляции, остаточные средние квадратические отклонения и дисперсии, объемы выборок;
8) таблица выбора эффективной модели и ее значимости по отношению к стационарной выборке с результатами расчетов;
9) вывод о наличии или отсутствии климатических изменений в рассматриваемом ряду климатической характеристики.

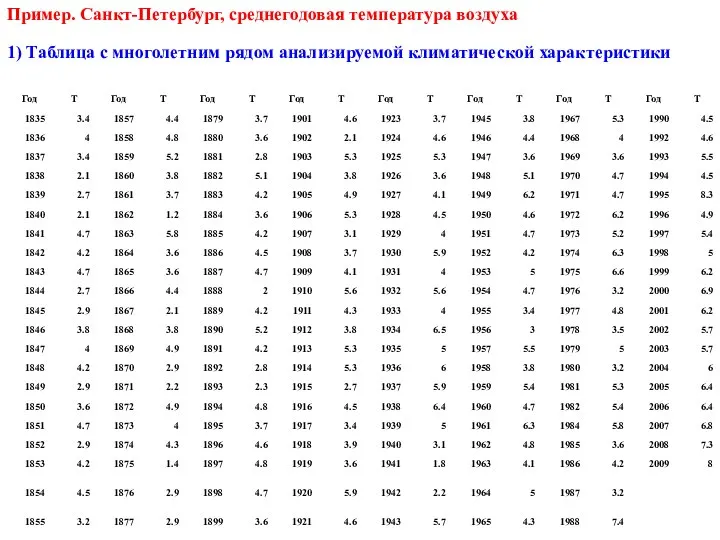
1) Таблица с многолетним рядом анализируемой климатической характеристики
Пример. Санкт-Петербург, среднегодовая температура воздуха

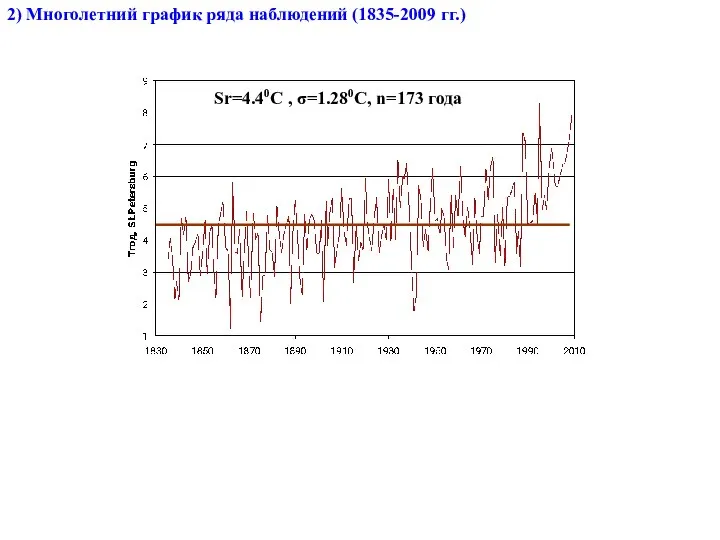
2) Многолетний график ряда наблюдений (1835-2009 гг.)
Sr=4.40С , σ=1.280С, n=173 года

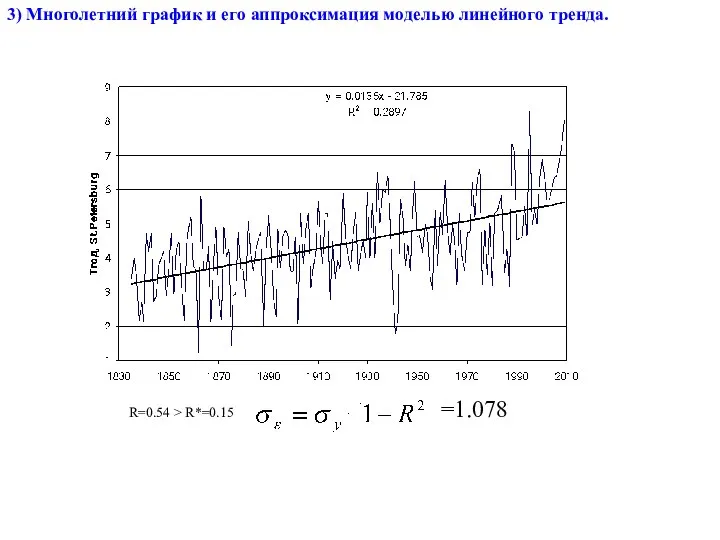
3) Многолетний график и его аппроксимация моделью линейного тренда.
R=0.54 > R*=0.15
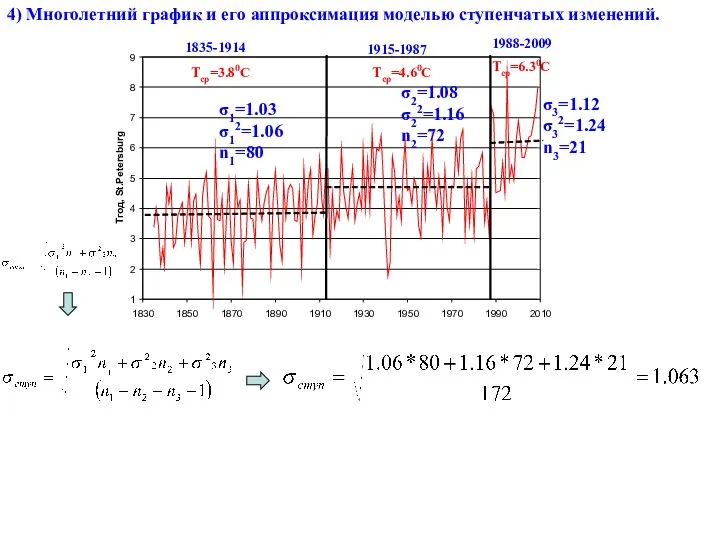
=1.078

4) Многолетний график и его аппроксимация моделью ступенчатых изменений.
1835-1914
1915-1987
1988-2009
Tср=3.80C
Tср=4.60C
Tср=6.30C
σ1=1.03
σ12=1.06
n1=80
σ2=1.08
σ22=1.16
n2=72
σ3=1.12
σ32=1.24
n3=21

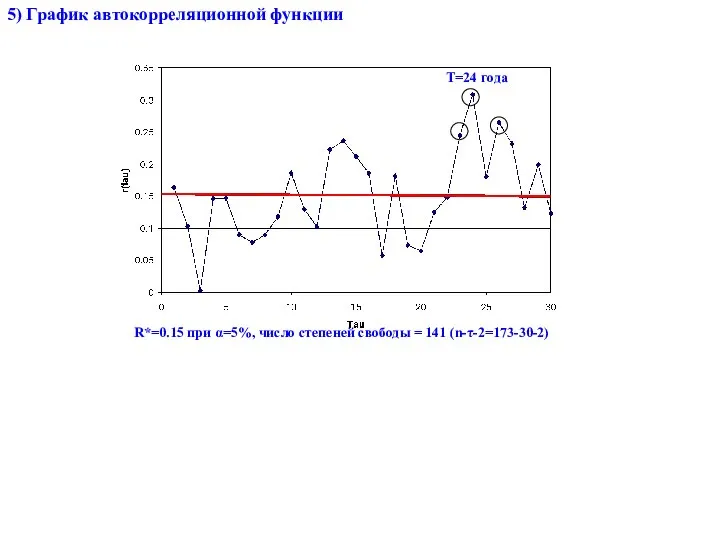
5) График автокорреляционной функции
R*=0.15 при α=5%, число степеней свободы = 141 (n-τ-2=173-30-2)
T=24 года

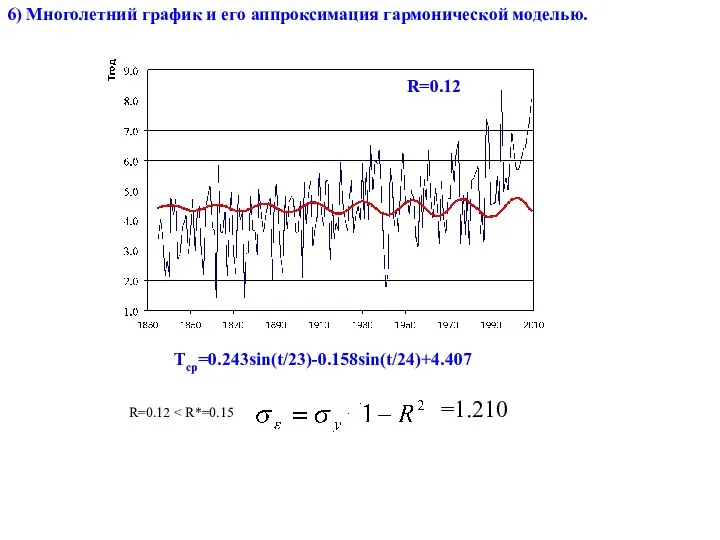
6) Многолетний график и его аппроксимация гармонической моделью.
Tср=0.243sin(t/23)-0.158sin(t/24)+4.407
R=0.12
R=0.12 < R*=0.15
=1.210

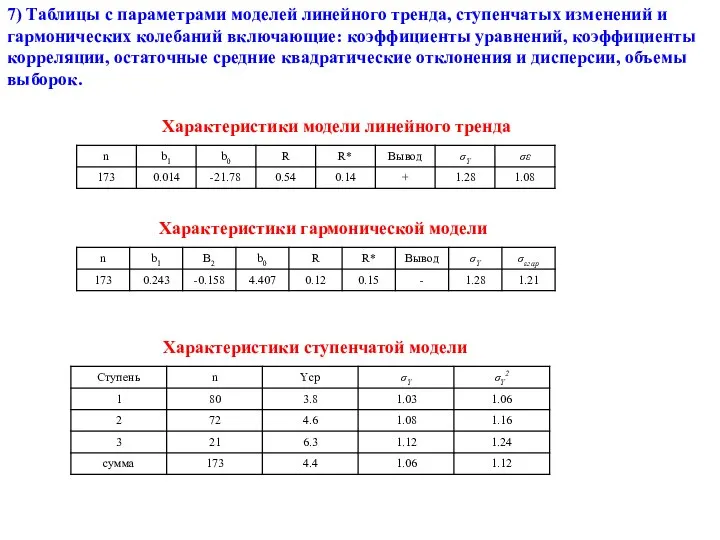
7) Таблицы с параметрами моделей линейного тренда, ступенчатых изменений и гармонических колебаний включающие: коэффициенты уравнений, коэффициенты корреляции, остаточные средние квадратические отклонения и дисперсии, объемы выборок.
Характеристики модели линейного тренда
Характеристики гармонической модели
Характеристики ступенчатой модели

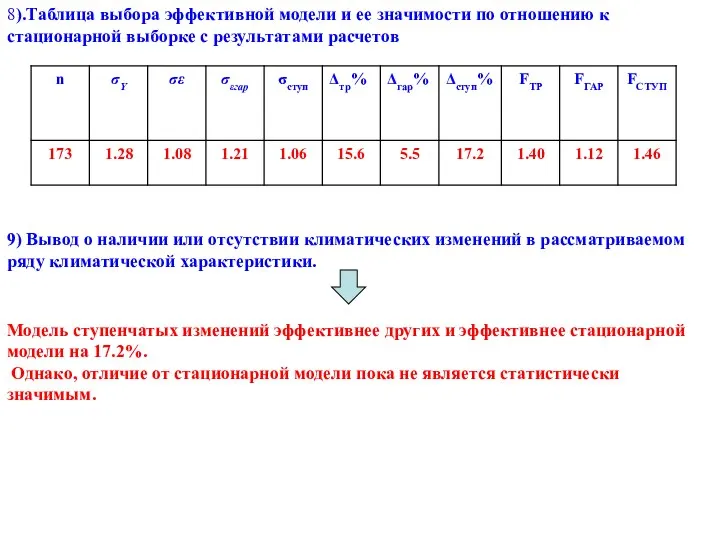
8).Таблица выбора эффективной модели и ее значимости по отношению к стационарной выборке с результатами расчетов
9) Вывод о наличии или отсутствии климатических изменений в рассматриваемом ряду климатической характеристики.
Модель ступенчатых изменений эффективнее других и эффективнее стационарной модели на 17.2%.
Однако, отличие от стационарной модели пока не является статистически значимым.

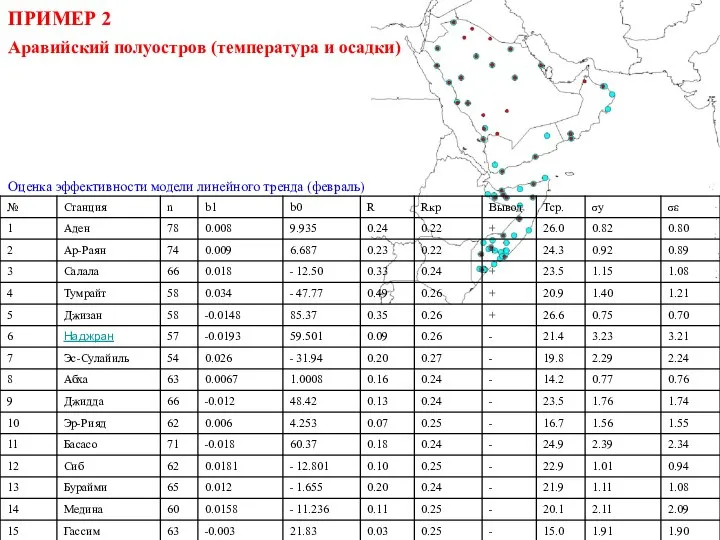
Оценка эффективности модели линейного тренда (февраль)
ПРИМЕР 2
Аравийский полуостров (температура и осадки)

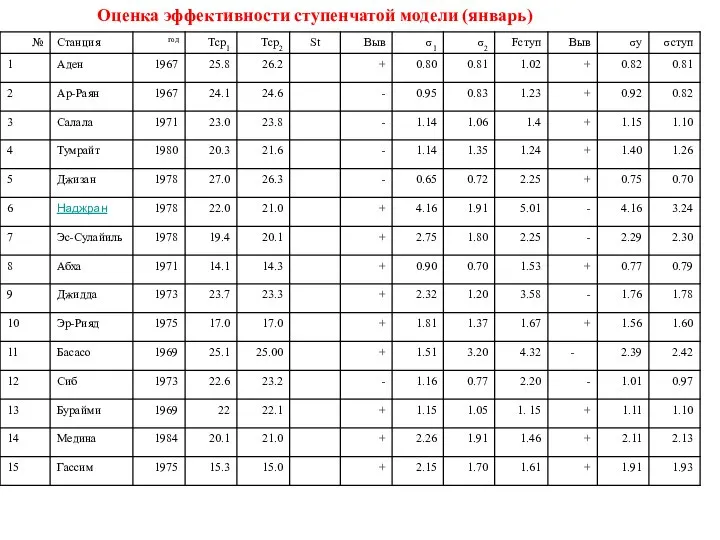
Оценка эффективности ступенчатой модели (январь)