Содержание
- 2. У Х 1 1 -1 -1 I II III IV 1. Повторяем понятия прямоугольной системы координат,
- 3. Построение точки по ее координатам У Х О М (-3;2) -3 2 Пример: построить точку М(-3;2)
- 4. Определение функции Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное
- 5. Графический способ задания функции Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям
- 6. Функция у = kх Графиком функции у = kх при любом значении k является прямая, проходящая
- 7. Расположение графика функции у = kх в координатной плоскости зависит от коэффициента k. х у k
- 8. Прямая пропорциональная зависимость Если х>0, у>0 и k>0, то зависимость между переменными х и у, выражаемую
- 10. Скачать презентацию
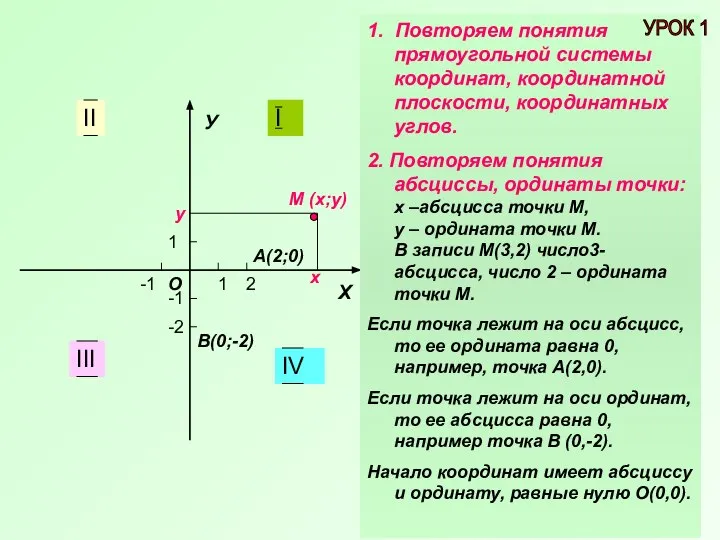
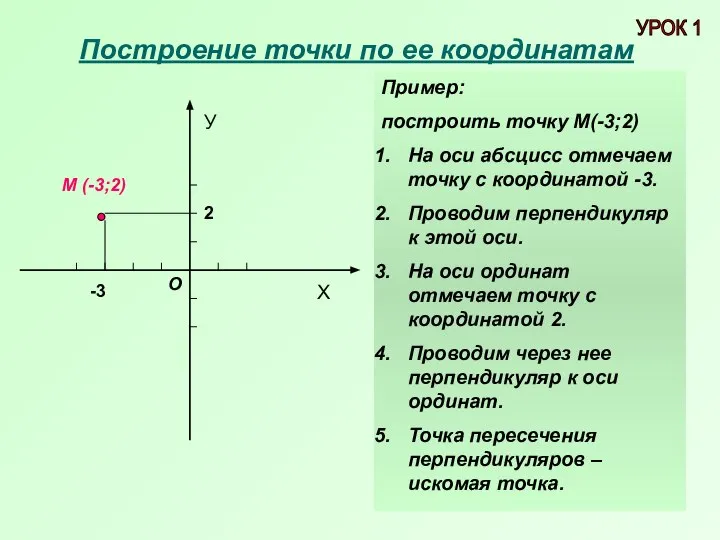



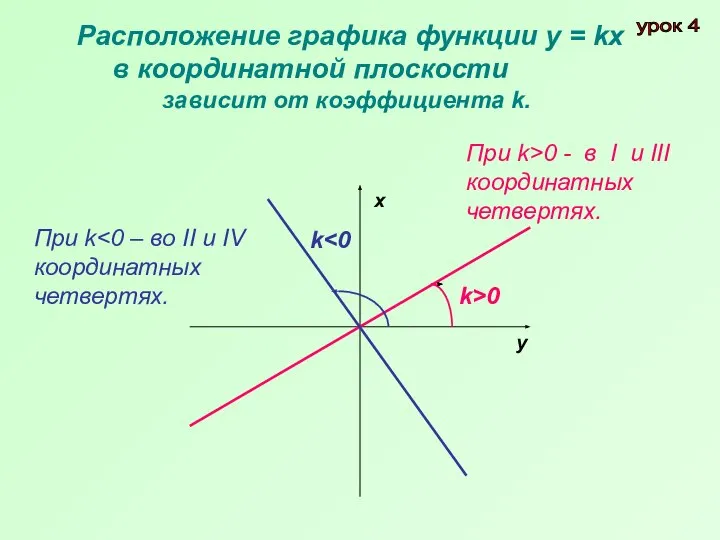

 Схема Горнера
Схема Горнера Индивидуальное задание №8. Построение линии пересечения тора и конуса
Индивидуальное задание №8. Построение линии пересечения тора и конуса Математика в играх и задачах
Математика в играх и задачах Призмы и антипризмы
Призмы и антипризмы Степенная функция и ее график
Степенная функция и ее график Задачи на перебор вариантов. 4 класс
Задачи на перебор вариантов. 4 класс Параллельные прямые
Параллельные прямые Решение уравнений с помощью разложения на множители
Решение уравнений с помощью разложения на множители Предельные величины, эластичности
Предельные величины, эластичности Несобственные интегралы. Лекция 5
Несобственные интегралы. Лекция 5 Круглые числа. Величина
Круглые числа. Величина Задача на тему: Прогрессия
Задача на тему: Прогрессия Системы линейных дифференциальных уравнений
Системы линейных дифференциальных уравнений Системы линейных алгебраических уравнений (СЛАУ)
Системы линейных алгебраических уравнений (СЛАУ) Презентация на тему Призма
Презентация на тему Призма  predel-posledovatelnosti-svoystva-i
predel-posledovatelnosti-svoystva-i Абсолютная величина
Абсолютная величина Своя игра. Показательная и степенная функции. 10 класс
Своя игра. Показательная и степенная функции. 10 класс Куб. Теорема Эйлера
Куб. Теорема Эйлера Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел Великолепная пятерка. Игра
Великолепная пятерка. Игра 2._3
2._3 Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Арифметика в позиционных системах счисления
Арифметика в позиционных системах счисления Длина. Сантиметр
Длина. Сантиметр Дифференциальные уравнения. Лекция 2
Дифференциальные уравнения. Лекция 2 Измерение углов. Транспортир
Измерение углов. Транспортир Умножение десятичной дроби на обыкновенную
Умножение десятичной дроби на обыкновенную