Морфизмы алгебр

Будем рассматривать однотипные алгебры А =〈A; ΩF〉 и В =〈B, ΩG〉, где ΩF = (F1, F2, …, Fn), τ =(m1,m2,…,mn), mi – число аргументов Fi ; ΩG = (G1, G2, …, Gn), τ =(m1,m2,…,mn), mi – число аргументов Gi . Таким образом, рассматриваем алгебры, в каждой из которых введены одинаковые числа (n) операций и для каждого i, 1≤ i ≤ n, числа аргументов операций Fi и Gi одинаковы. Всякое отображение ϕ основного множества А в(на) основное множество В называем отображением алгебры А в(на) алгебру В.

Изоморфизмом алгебры А =〈A; F1, F2, …, Fn〉 в (на) однотипную алгебру В =〈B; G1, G2, …, Gn〉 называется взаимно однозначное (биективное) отображение ϕ множества А в(на) В, сохраняющее главные операции алгебры, т.е. для которого выполняются соотношения: ϕ(Fi(x1, x2, …, xmi ))=Gi(ϕ(x1), …, ϕ(xmi )) (2.1) для всех i, 1≤ i ≤ n, и для любых x1, x2,…, xmi∈A. Изоморфизм алгебры на себя называется автоморфизмом. Гомоморфизмом алгебры А =〈A; F1, F2, …, Fn〉 в(на) однотипную алгебру В =〈B; G1, G2, …, Gn〉 называется отображение ϕ множества А в(на) множество В, сохраняющее главные операции алгебры, т.е. для которого выполняются условия (2.1) для всех i, 1≤ i ≤ n, и для любых x1, x2,…, xmi∈A.

ПРИМЕРЫ
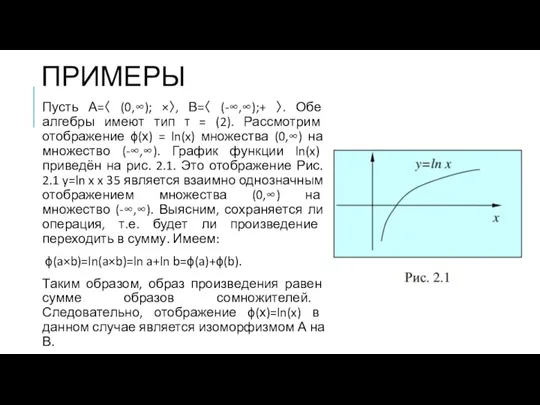
Пусть А=〈 (0,∞); ×〉, В=〈 (-∞,∞);+ 〉. Обе алгебры имеют тип τ = (2). Рассмотрим отображение ϕ(х) = ln(x) множества (0,∞) на множество (-∞,∞). График функции ln(x) приведён на рис. 2.1. Это отображение Рис. 2.1 y=ln x x 35 является взаимно однозначным отображением множества (0,∞) на множество (-∞,∞). Выясним, сохраняется ли операция, т.е. будет ли произведение переходить в сумму. Имеем:
ϕ(a×b)=ln(a×b)=ln a+ln b=ϕ(a)+ϕ(b).
Таким образом, образ произведения равен сумме образов сомножителей. Следовательно, отображение ϕ(х)=ln(x) в данном случае является изоморфизмом А на В.

Пусть А =〈 (0,∞); + 〉, В=〈 (-∞,∞); ×〉. Введем отображение ϕ(х)=е х . График функции е х приведён на рис. 2.2. Тогда имеем:
ϕ(х+у) = е х+у = е х ⋅е у = ϕ(х)⋅ϕ(у).
Таким образом, образ суммы равен произведению образов. Следовательно, это отображение является изоморфизмом А в В, так как ϕ отображает взаимно однозначно множество (0,∞) на часть множества (-∞,∞), ибо е х >1 .

Пусть М - множество квадратных n×n матриц действительных чисел и на М введена операция умножения матриц, т.е. имеем алгебру А =〈M; ×〉 типа τ = (2). Положим, что В =〈 (-∞,∞);•〉, здесь «•» означает обычное умножение чисел. Введем отображение ϕ(С)=det(С), когда матрице С ставится в соответствие ее определитель (det(С)). Очевидно, имеем
ϕ(С×D)= det(C×D)= detС• detD= ϕ(C)• ϕ(D).
Таким образом, отображение ϕ: А → В сохраняет операцию. Но это отображение не является изоморфным, так как различные матрицы могут иметь одинаковый определитель. Итак, ϕ – гомоморфизм А на В.