Функция распределения дискретной случайной величины

Определение
Еще одной геометрической иллюстрацией дискретной случайной величины является ее функция распределения.
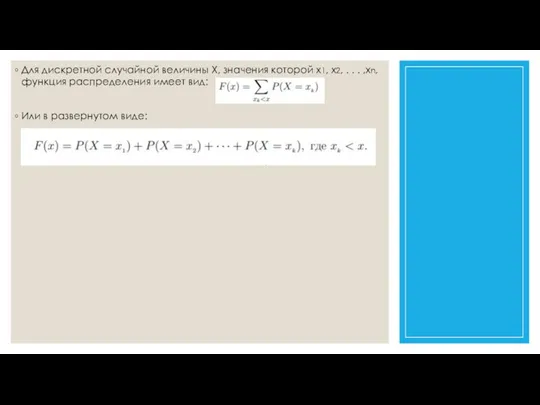
Определение. Функцией распределения случайной величины называется функция, которая в каждой точке x числовой прямой определяет вероятность события, в котором случайная величина принимает значение, меньшее, чем x.
То есть1 , F(x) = P(X < x).
Таким образом, вероятность того, что X < x зависит от x, поэтому функция F(x) называется функцией распределения2
С точки зрения геометрии функция распределения определяет вероятность того, что случайная величина X в результате исхода попадет на координатную прямую левее x:
1Под выражением P(X < x) следует понимать вероятность события ω, в котором случайная величина принимает значение меньшее, чем x. Или в обозначениях x:
2 В старых учебниках по теории вероятностей, а также в приложениях функцию распределения называют кумулятивной функцией или накопительной функцией. Такое название вытекает из ее определения: из него видно, как накапливается «количество вероятности»

Для дискретной случайной величины X, значения которой x1, x2, . . . ,xn, функция распределения имеет вид:
Или в развернутом виде:

При табличном задании значения случайной величины упорядочивают по возрастанию, записывая в первой строке таблицы, а соответствующие значения вероятностей располагают во второй ее строке:
Построим график функции распределения F(x) случайной величины X, заданной табличным законом распределения:

Функция распределения имеет неустранимые разрывы первого рода слева в тех точках, в которых дискретная случайная величина Х принимает возможные значения, указанные в таблице закона распределения.
В интервалах между возможными значениями случайной величины функция F(x) является постоянной.
Сумма скачков функции распределения равна единице.
График функции распределения дискретной случайной величины есть разрывная ступенчатая функция: