Содержание
- 2. Генеральная и выборочная совокупность Генеральная совокупность – это совокупность объектов, из которой производится выборка. Объем совокупности
- 3. Пример С завода на склад поступило 10 тыс. деталей. Необходимо исследовать их на наличие дефектов. Все
- 4. Точечные оценки Необходимо определить значение неизвестного параметра ? распределения случайной величины X по выборке x1, x2,
- 5. Интервальные оценки Интервальной оценкой называют оценку, определяющуюся двумя концами интервала. При выборке малого объема точечная оценка
- 6. Несмещенная оценка Несмещенная оценка – это точечная оценка математического ожидания, которая равна оценивающему параметру. Оценка ?*
- 7. Генеральная средняя Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя Выборочная средняя
- 8. Из генеральной совокупности извлечена выборка объема n, заданная вариантами Хi и соответствующими им частотами. Найти несмещенную
- 9. Условные варианты Предположим, что варианты выборки расположены в возрастающем порядке, т. е. в виде вариационного ряда.
- 10. Условными называют варианты, определяемые равенством ui=(xi-C)/h, где С—ложный нуль (новое начало отсчета); h — шаг, т.
- 11. Пример. Найти условные варианты статистического распределения: варианты . . . 23,6 28,6 33,6 38,6 43,6 частоты
- 12. Генеральная дисперсия Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их
- 14. Выборочная дисперсия Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).
- 15. Выборочная дисперсия при различии всех значений варианта выборки находится по формуле: Для значений признаков выборочной совокупности
- 16. Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика
- 17. Пример 1 Найти выборочную дисперсию выборки со значениями: xi: 1, 2, 3, 4; ni: 20, 15,
- 18. Исправленная дисперсия Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S2. Среднеквадратическая генеральная совокупность
- 19. Пример Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины:
- 20. Выборочная совокупность задана следующей таблицей распределения: Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную
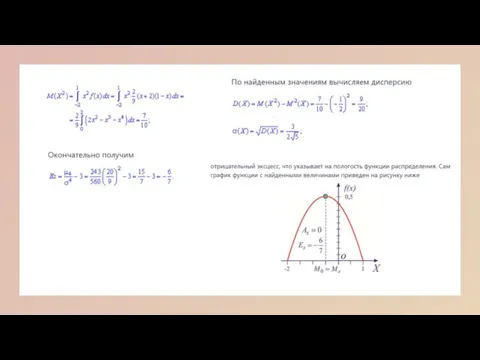
- 21. Асимметрия. Эксцесс. Вычисление асимметрии и эксцесса позволяет установить симметричность распределения случайной величины X относительно M(X)=1. Для
- 22. Пример
- 25. Скачать презентацию





















 Равнобедренный треугольник
Равнобедренный треугольник Математическое моделирование
Математическое моделирование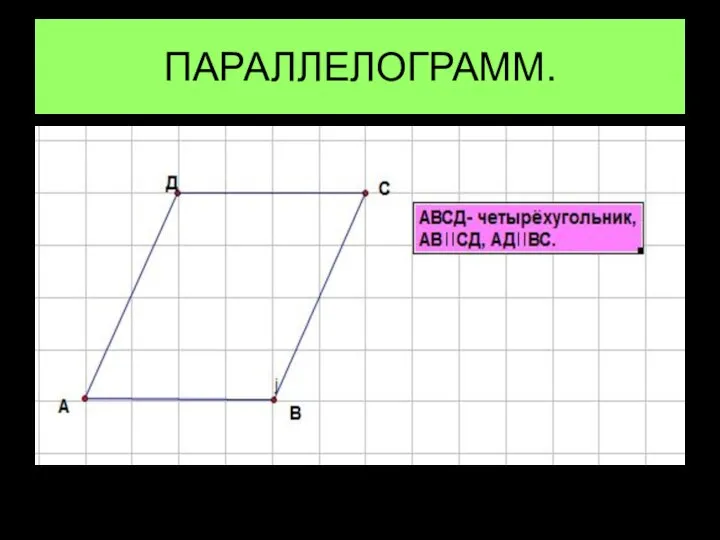 Параллелограмм. Свойства. Признаки
Параллелограмм. Свойства. Признаки Презентация на тему Использование здоровьесберегающих технологий на уроках математики
Презентация на тему Использование здоровьесберегающих технологий на уроках математики  Элементы математической статистики
Элементы математической статистики Письменное умножение трёхзначного числа на однозначное
Письменное умножение трёхзначного числа на однозначное Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1)
Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1) Осевая и центральная симметрии
Осевая и центральная симметрии Геометрическая прогрессия
Геометрическая прогрессия Нумерация. Подготовка к ВПР
Нумерация. Подготовка к ВПР Логарифмы. История возникновения логарифмов
Логарифмы. История возникновения логарифмов Теория множеств
Теория множеств Великие математики древности. Архимед, Пифагор, Евклид, Фалес
Великие математики древности. Архимед, Пифагор, Евклид, Фалес Деление дробей. Путешествие в Китай
Деление дробей. Путешествие в Китай Расстояние от точки до фигуры
Расстояние от точки до фигуры Однородные системы линейных алгебраических уравнений
Однородные системы линейных алгебраических уравнений Презентация на тему Теорема о сумме углов треугольника
Презентация на тему Теорема о сумме углов треугольника  Перехідна та імпульсна перехідна функції
Перехідна та імпульсна перехідна функції Решение уравнений, содержащих параметры
Решение уравнений, содержащих параметры Взаимное расположение двух окружностей
Взаимное расположение двух окружностей Презентация на тему Сравнение дробей (5 класс)
Презентация на тему Сравнение дробей (5 класс)  Случаи сложения и вычитания основанные на знаниях нумерации
Случаи сложения и вычитания основанные на знаниях нумерации Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Методика изучения длины в процессе изучения геометрического материала
Методика изучения длины в процессе изучения геометрического материала Формула полной вероятности и формула Байеса
Формула полной вероятности и формула Байеса Арккосинус а. Решение уравнений
Арккосинус а. Решение уравнений Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Задачи с параметрами.Расположение корней квадратного трёхчлена
Задачи с параметрами.Расположение корней квадратного трёхчлена