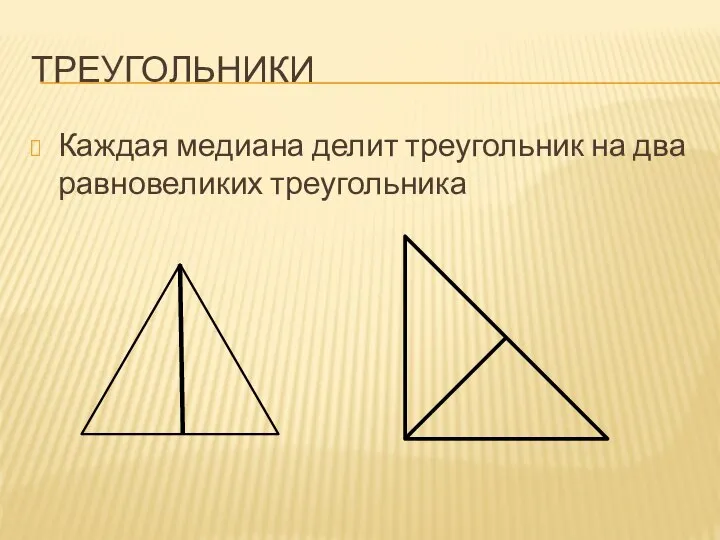
Слайд 3ТРЕУГОЛЬНИКИ
Каждая медиана делит треугольник на два равновеликих треугольника
Слайд 4ТРЕУГОЛЬНИКИ
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис

Слайд 5ТРЕУГОЛЬНИКИ
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников

относятся как произведения сторон, заключающих равные углы
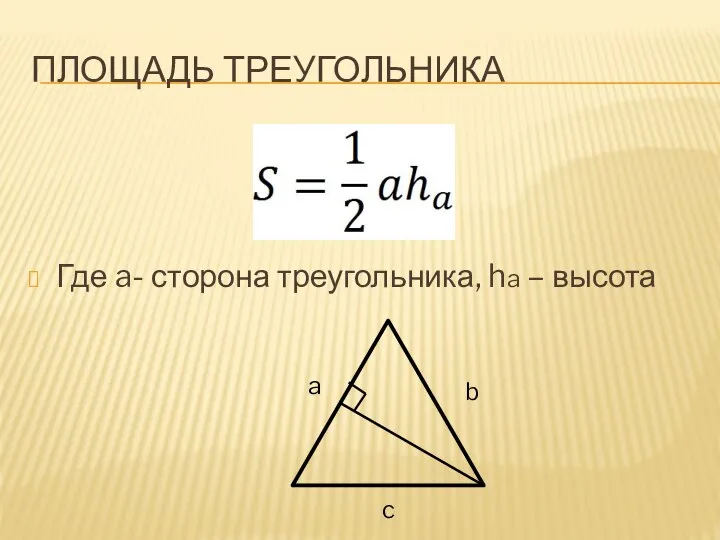
Слайд 6ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Где a- сторона треугольника, ha – высота
a
b
c
Слайд 7ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Где b, c- стороны треугольника, и угол A- лежит против стороны

a
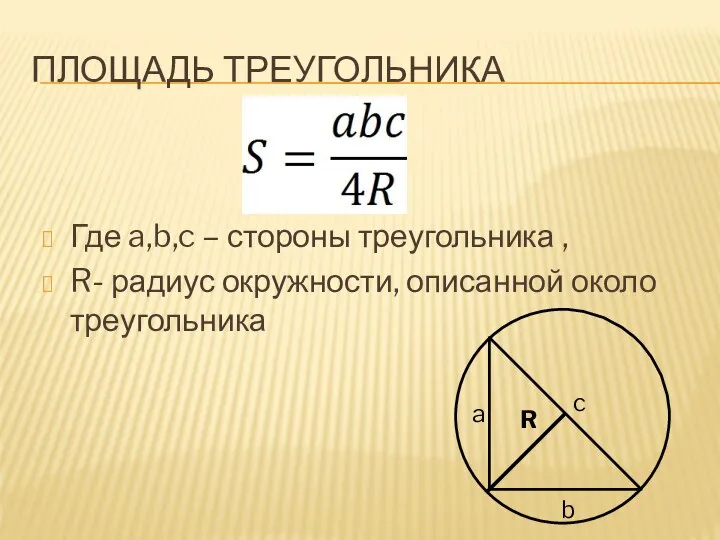
Слайд 8ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Где a,b,c – стороны треугольника ,
R- радиус окружности, описанной около треугольника
R
Слайд 9ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Где r –радиус вписанной окружности,
p- полупериметр

Слайд 10ПЛОЩАДЬ ТРЕУГОЛЬНИКА (ФОРМУЛА ГЕРОНА)
Где a,b,c – стороны треугольника
p– полупериметр треугольника

Слайд 13ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Радиус окружности описанной около прямоугольного треугольника равен половине гипотенузы
R

Слайд 14ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Сумма острых углов прямоугольного треугольника равно 900
Катет прямоугольного треугольника, лежащий против

угла в 300, равен половине гипотенузы
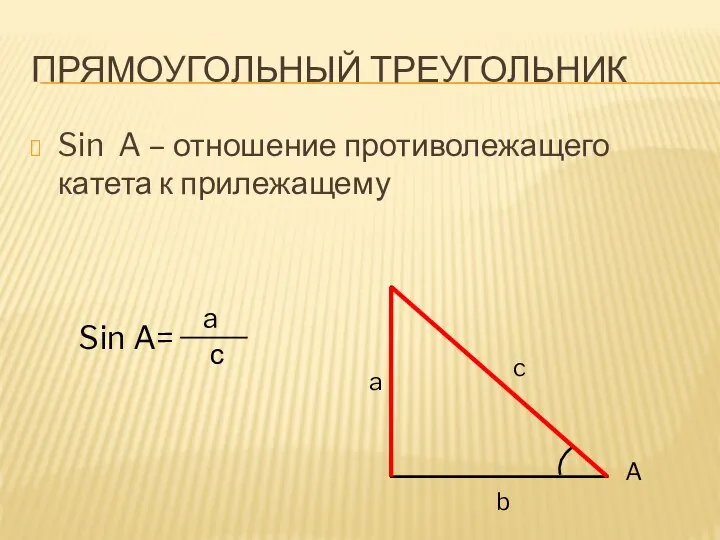
Слайд 15ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Sin A – отношение противолежащего катета к прилежащему
A
Sin A=
a
с
Слайд 16ПРЯМОУГОЛЬНЫЙ ТЕУГОЛЬНИК
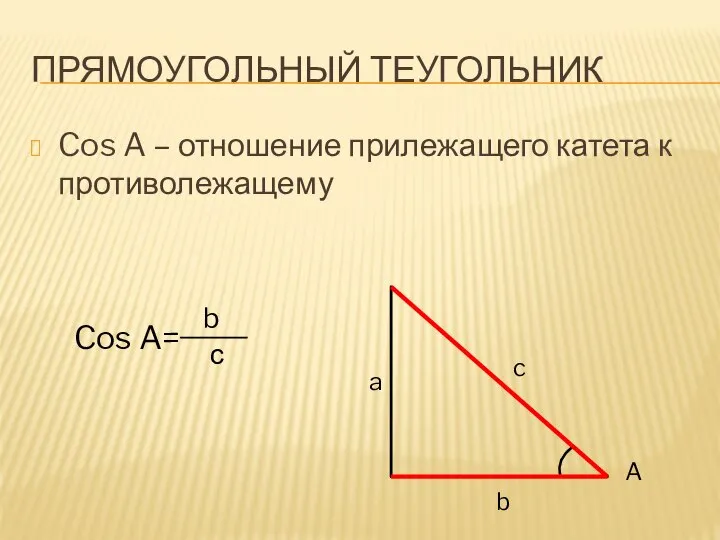
Cos A – отношение прилежащего катета к противолежащему
A
Cos A=
b
с
Слайд 17ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Tg A – отношение противолежащего катета к прилежащему
A
tg A=
a
b

Слайд 18ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
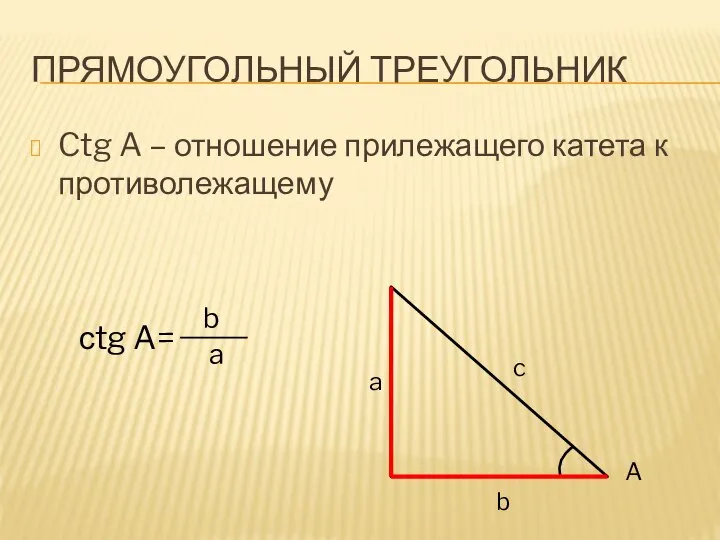
Ctg A – отношение прилежащего катета к противолежащему
сtg A=
b
a
A
Слайд 19РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
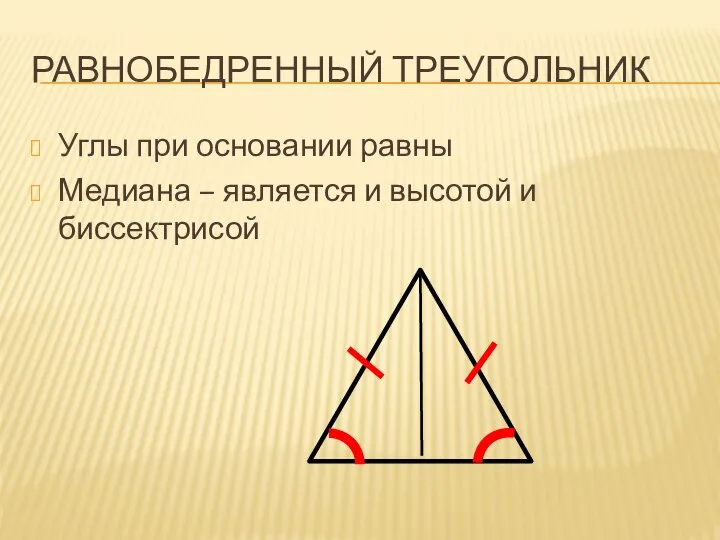
Углы при основании равны
Медиана – является и высотой и биссектрисой
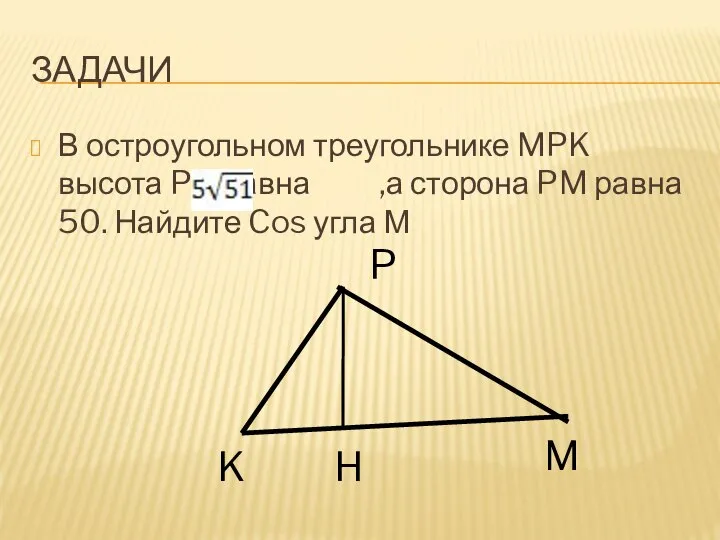
Слайд 20ЗАДАЧИ
В остроугольном треугольнике MPK высота PH равна ,а сторона PM равна 50.
Слайд 21ЗАДАЧИ
В треугольнике АВС АВ = ВС. Угол САВ = 34о. Найдите угол

между стороной АВ и высотой, проведенной из вершины В.
Слайд 22ЗАДАЧИ
В треугольнике АВС проведена высота ВК = 12 см. Известно, что синус

угла САВ равен 0,6. Найдите длину стороны АВ. Ответ дайте в см.
Слайд 23ЗАДАЧИ
Стороны AC, AB, BC треугольника ABC равны 2√5, √11 и 2 соответственно. Точка K расположена вне

треугольника AB, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC>90
Слайд 24ЗАДАЧИ
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится
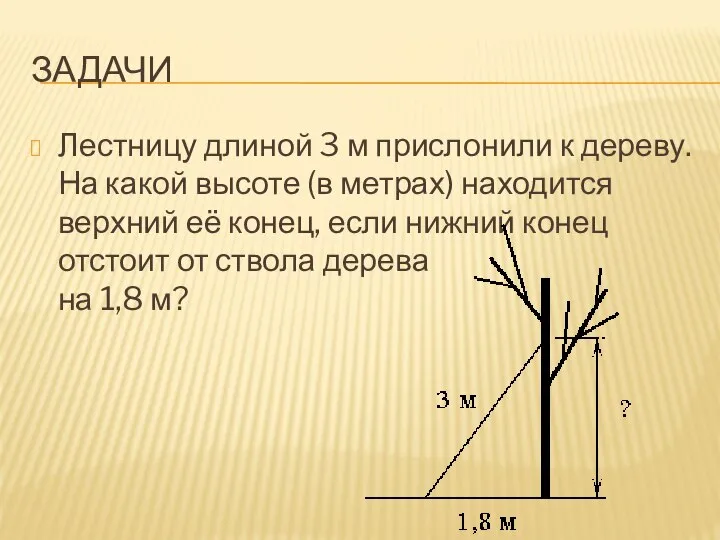
верхний её конец, если нижний конец отстоит от ствола дерева
на 1,8 м?
Слайд 25ЗАДАЧИ
В равностороннем треугольнике ABC точки M, N, K —— середины сторон АВ, ВС,
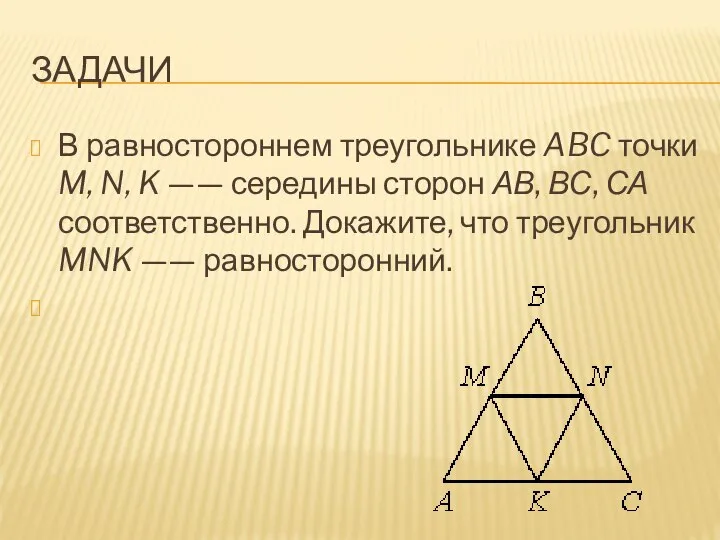
СА соответственно. Докажите, что треугольник MNK —— равносторонний.
























 Диаграммы
Диаграммы Проекты сезона 2020-21
Проекты сезона 2020-21 Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Функция
Функция Функции. Их свойства
Функции. Их свойства Арифметическая прогрессия
Арифметическая прогрессия Окружность. Круг
Окружность. Круг Чётные и нечётные функции
Чётные и нечётные функции Действия с алгебраическими дробями
Действия с алгебраическими дробями Математическое ралли. Итоговое повторение 5 класс
Математическое ралли. Итоговое повторение 5 класс Линейная зависимость и линейная независимость системы векторов. Семинар 4
Линейная зависимость и линейная независимость системы векторов. Семинар 4 Ккомбинаторика. Перестановки. Размещения. Сочетания
Ккомбинаторика. Перестановки. Размещения. Сочетания Многогранники. Вершины, рёбра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера
Многогранники. Вершины, рёбра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера Задания со спичками
Задания со спичками Презентация на тему Свойства числовых неравенств
Презентация на тему Свойства числовых неравенств  Построение треугольника
Построение треугольника Основные сведения о матрицах. Операции над матрицами
Основные сведения о матрицах. Операции над матрицами Исследование функций
Исследование функций Точка и прямая на чертежах
Точка и прямая на чертежах Объемы и поверхности многогранников
Объемы и поверхности многогранников Линейная алгебра. Определители
Линейная алгебра. Определители Вычисление производных с помощью правил дифференцирования
Вычисление производных с помощью правил дифференцирования Конус
Конус Несобственные интегралы первого рода
Несобственные интегралы первого рода Шар и сфера
Шар и сфера ЕГЭ Профиль - Задание 6
ЕГЭ Профиль - Задание 6 Поверхности и тела. Проецирование геометрических фигур
Поверхности и тела. Проецирование геометрических фигур Построение графиков функций. Алгебра и начала анализа 11 класс
Построение графиков функций. Алгебра и начала анализа 11 класс