Содержание
- 2. Совокупность элементов, объединённых некоторым признаком, свойством, составляет понятие множество. Например, множество книг в библиотеке, множество студентов
- 3. Множества удобно изображать с помощью кругов Эйлера. Множество K на рис. 1.1 называют подмножеством множества М
- 4. Универсальным называется множество U, состоящее из всех возможных элементов, обладающих данным признаком. Если множество не содержит
- 5. Множество, элементами которого являются подмножества множества М, называется семейством множества М или булеаном этого множества и
- 6. Множество считается заданным, если перечислены все его элементы, или указано свойство, которым обладают те и только
- 7. Примеры задания множества Множество всех чисел, являющихся неотрицательными степенями числа 2 можно задать: а) перечислением элементов:
- 8. Вместо выражения «любое х из множества Х» можно писать , где перевёрнутая латинская буква А взята
- 9. 1.4. Классификация множеств. Мощность множества Множество, содержащее конечное число элементов, называется конечным. Пустое множество является конечным
- 11. Скачать презентацию








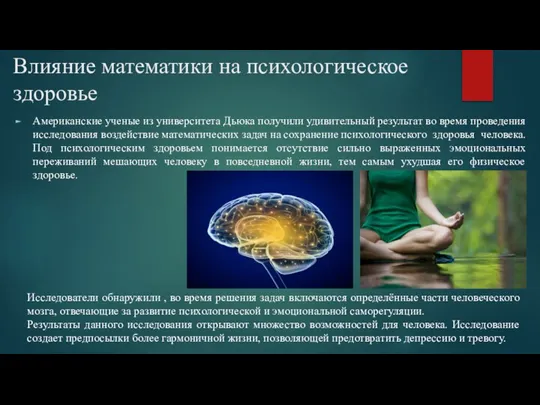 Влияние математики на психологическое здоровье
Влияние математики на психологическое здоровье Доли и дроби
Доли и дроби Презентация на тему Линейная функция и её график
Презентация на тему Линейная функция и её график  Презентация на тему Учим состав числа от 5 до 10
Презентация на тему Учим состав числа от 5 до 10  Презентация на тему Площадь: площадь трапеции
Презентация на тему Площадь: площадь трапеции  Описательная статистика
Описательная статистика Интерактивный тренажёр. Сложение и вычитание в пределах первого десятка
Интерактивный тренажёр. Сложение и вычитание в пределах первого десятка Решение логических задач
Решение логических задач Равенство
Равенство Решение систем неравенств (8 класс)
Решение систем неравенств (8 класс) Циклический алгоритм
Циклический алгоритм Презентация на тему Преобразования графиков функций
Презентация на тему Преобразования графиков функций  Вычитание вида 13
Вычитание вида 13 54 задачи на чертежах по планиметрии. Теорема Пифагора
54 задачи на чертежах по планиметрии. Теорема Пифагора Тригонометрические уравнения
Тригонометрические уравнения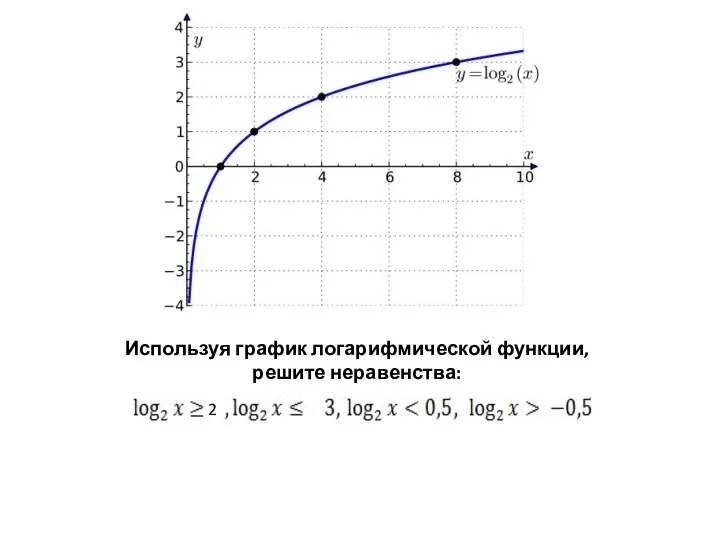 Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Интегрированный урок алгебры в 8 классе
Интегрированный урок алгебры в 8 классе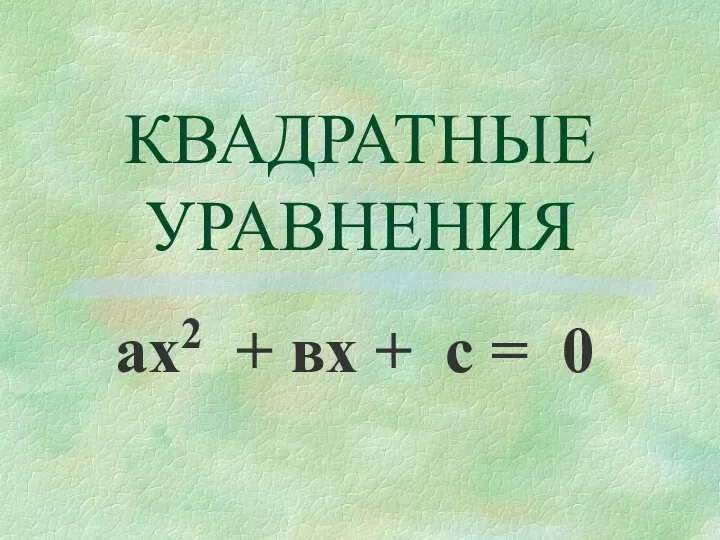 Квадратные уравнения ах2 + вх + с = 0
Квадратные уравнения ах2 + вх + с = 0 Объект и пространство
Объект и пространство Площадь параллелограмма
Площадь параллелограмма Урок математики
Урок математики Презентация на тему Число 8. Цифра 8
Презентация на тему Число 8. Цифра 8  Непрерывность функций
Непрерывность функций Нахождение конуса в природе
Нахождение конуса в природе Неполные квадратные уравнения
Неполные квадратные уравнения Повторение пройденного материала
Повторение пройденного материала ГИА - 2016. Открытый банк заданий по математике. Задача №15
ГИА - 2016. Открытый банк заданий по математике. Задача №15 Устный счёт Прицепи вагоны. 2 класс
Устный счёт Прицепи вагоны. 2 класс