Слайд 2Раздел 4. Дифференциальное исчисление функции одной переменной
Тема 7. Производная и дифференциал
Лекция 7.1.

Понятие производной
Слайд 3Учебные цели:
1. Раскрыть содержание понятия производной.
2. Рассмотреть геометрический и физический смысл производной.
3.

Сформировать представление о производных основных элементарных функций, правилах дифференцирования, производной сложной функции.
Слайд 4Учебные вопросы:
1. Определение производной
2. Геометрический и физический смысл производной.
3. Правила дифференцирования. Производная

сложной функции.
Слайд 5Начиная с сегодняшней лекции, мы переходим к изучению основных положений дифференциального исчисления

– раздела математики, в котором изучаются производные и дифференциалы функций и их применение к исследованию функций. Оформление дифференциального исчисления в самостоятельную математическую дисциплину связано с именами И.Ньютона (1643 – 1727) и Г.Лейбница (1646 – 1716), проводившими исследования независимо друг от друга.
Слайд 6Создание дифференциального исчисления (наряду с интегральным исчислением) открыло новую эпоху в развитии

математики. Оно повлекло за собой появление ряда математических дисциплин: теории рядов, теории дифференциальных уравнений, дифференциальной геометрии и вариационного исчисления. Методы математического анализа нашли применение во всех разделах математики и других точных наук. Благодаря дифференциальному исчислению неизмеримо расширилась область приложений математики к вопросам естествознания и техники.
Слайд 7
Центральным аппаратом дифференциального исчисления служат понятия производной и дифференциала. Понятие производной возникло

из большого числа задач естествознания и математики, приводящихся к вычислению пределов отношений некоторого типа бесконечно малых. Важнейшие из них – построение касательной к кривой и определение скорости движения точки.
На сегодняшней лекции мы изучим понятие производной, геометрический и физический смысл производной, правила дифференцирования, в том числе правила дифференцирования сложных функций.
Слайд 8Вопрос 1. Определение производной
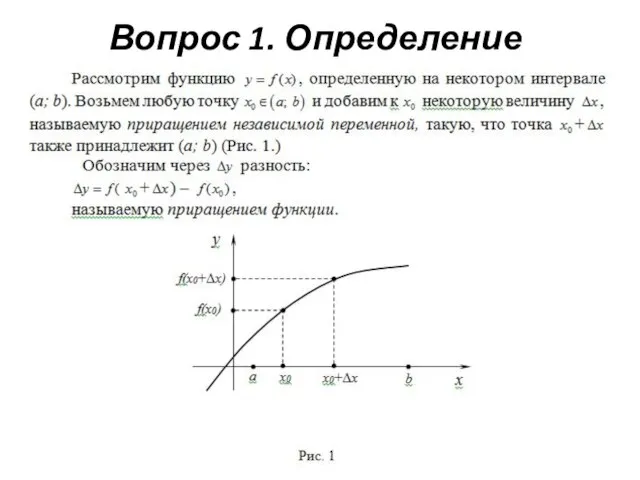
Слайд 11Видим, что процесс нахождения производной по ее определению достаточно трудоемкий. Его применяют

только для доказательства основных правил дифференцирования и формул для производных основных элементарных функций, которые сведены в таблицу производных.
Слайд 15Вопрос 2. Геометрический и физический смысл производной
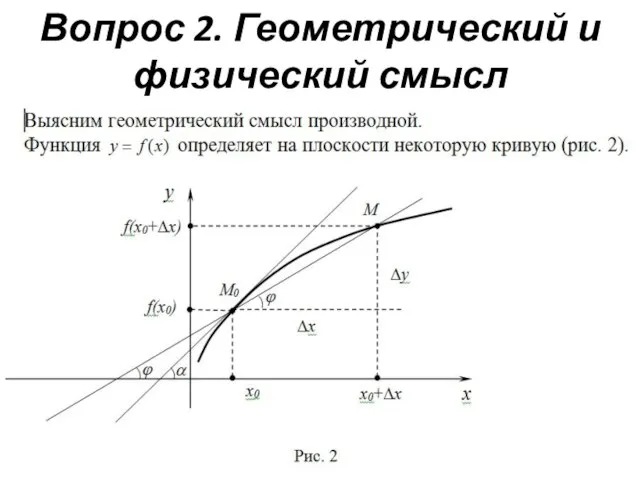
Слайд 21Вопрос 3. Правила дифференцирования. Производная сложной функции
























 Основы математической статистики в метрологии. Часть 2
Основы математической статистики в метрологии. Часть 2 Вероятность и статистика 11 кл
Вероятность и статистика 11 кл Правильная пирамида
Правильная пирамида Двоичная система счисления
Двоичная система счисления Производная сложной функции. Исследование функции с помощью производной. Дифференциал
Производная сложной функции. Исследование функции с помощью производной. Дифференциал Презентация на тему Неполные квадратные уравнения
Презентация на тему Неполные квадратные уравнения  Acrsin. Решение уравнений sint=a
Acrsin. Решение уравнений sint=a Примеры на состав числа 6
Примеры на состав числа 6 Правильные многогранники в природе
Правильные многогранники в природе Презентация на тему Вычитание суммы из числа и числа из суммы
Презентация на тему Вычитание суммы из числа и числа из суммы  Параллельность в пространстве
Параллельность в пространстве Повторительно-обобщающий урок по теме: Показательная функция. 11 класс
Повторительно-обобщающий урок по теме: Показательная функция. 11 класс Площадь треугольника
Площадь треугольника Учимся писать цифры
Учимся писать цифры Прямоугольный треугольник. Решение задач
Прямоугольный треугольник. Решение задач Знакомство с образованием чисел второго десятка
Знакомство с образованием чисел второго десятка Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа Алгебра. Задачник, часть 2
Алгебра. Задачник, часть 2 Сходимость несобственных интегралов второго рода от неотрицательных функций
Сходимость несобственных интегралов второго рода от неотрицательных функций Правила теории вероятности
Правила теории вероятности Единица измерения объёма жидкости-литр
Единица измерения объёма жидкости-литр Взаимное расположение прямой и окружности. 8 класс
Взаимное расположение прямой и окружности. 8 класс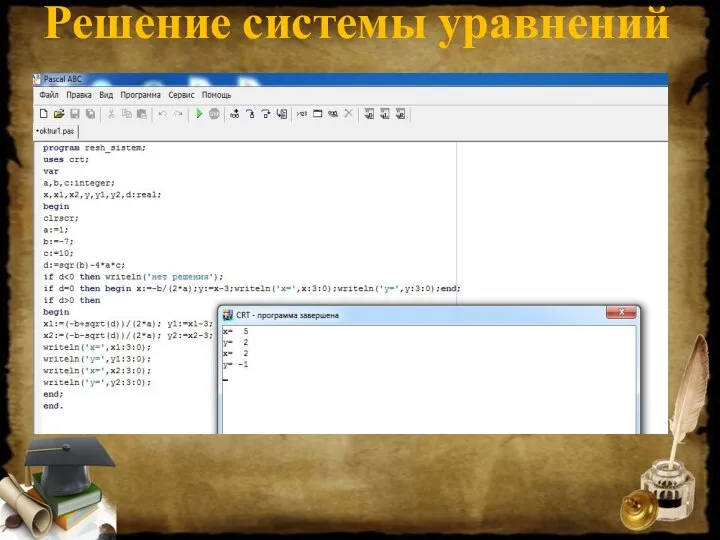 Решение системы уравнений. Задача на странный сюжет
Решение системы уравнений. Задача на странный сюжет Правильно оформляем работу
Правильно оформляем работу Деление на 2
Деление на 2 Связь между компонентами и результатом умножения. Чётные и нечётные числа
Связь между компонентами и результатом умножения. Чётные и нечётные числа Выбор плана эксперимента
Выбор плана эксперимента Презентация на тему Преобразование графиков функций
Презентация на тему Преобразование графиков функций