Содержание
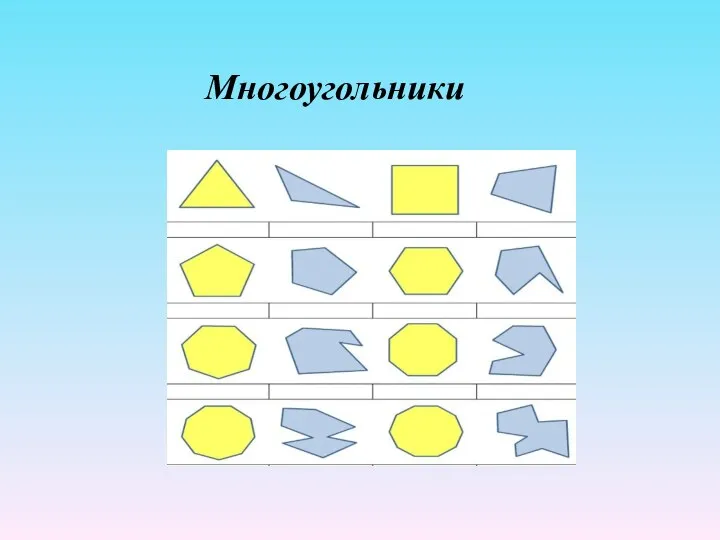
- 2. Многоугольники
- 3. 30.11.2012 www.konspekturoka.ru Задача Сколько сторон имеет многоугольник, если каждый угол которого равен 120°. Решение Так как
- 4. Четырехугольники Параллелограмм Прямоугольник Ромб Квадрат Трапеция
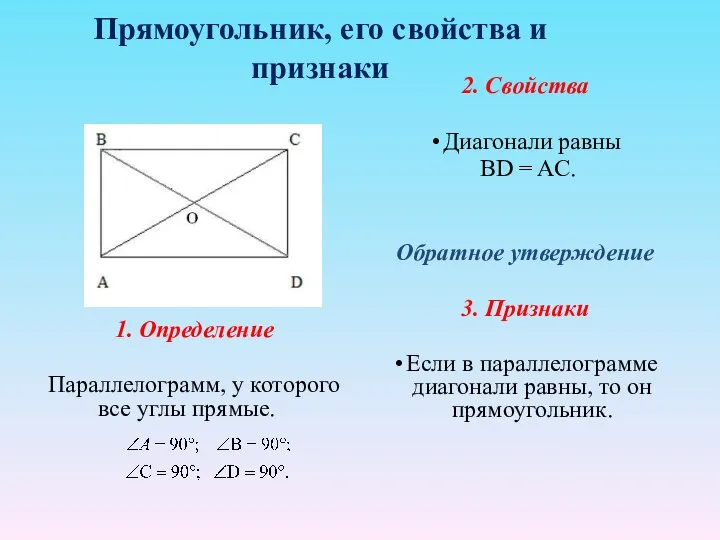
- 5. Прямоугольник, его свойства и признаки 1. Определение Параллелограмм, у которого все углы прямые. 2. Свойства Диагонали
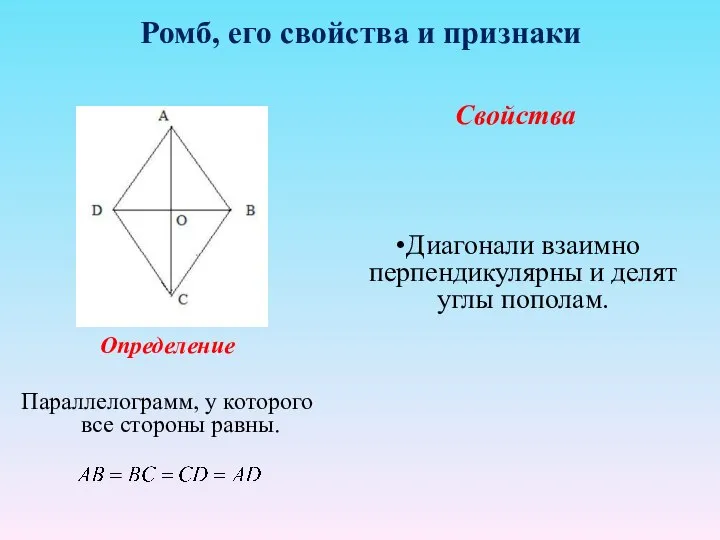
- 6. Ромб, его свойства и признаки Определение Параллелограмм, у которого все стороны равны. Свойства Диагонали взаимно перпендикулярны
- 7. Квадрат, его свойства и признаки Определение Прямоугольник, у которого все стороны равны. Свойства Диагонали равны, взаимно
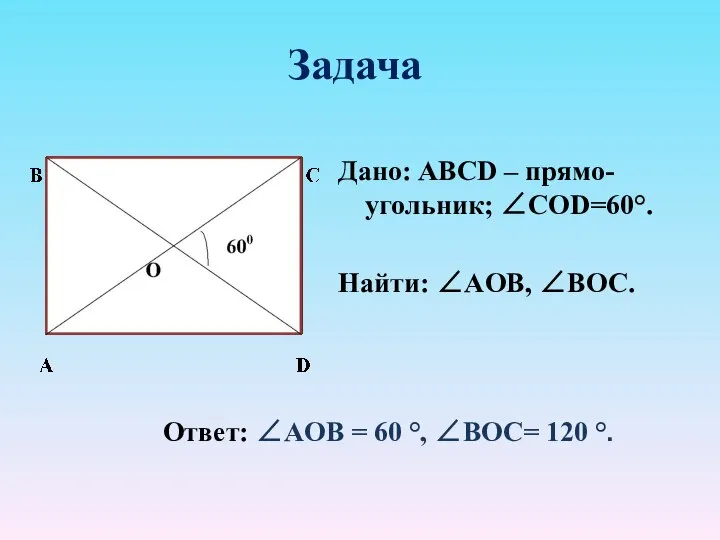
- 8. Задача Дано: ABCD – прямо-угольник; ∠CОD=60°. Найти: ∠АOB, ∠BOC. Ответ: ∠АOB = 60 °, ∠BOC= 120
- 9. Задача Дано: ABCD – прямоугольник; ∠ABD больше ∠СВD на 20°. Найти: углы треугольника АОD. Ответ: ∠А
- 10. Задача В ромбе угол между диагональю и стороной равен 25°. Найдите углы ромба. Ответ: 50°; 130°
- 11. Теорема Пифагора В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Это простота -
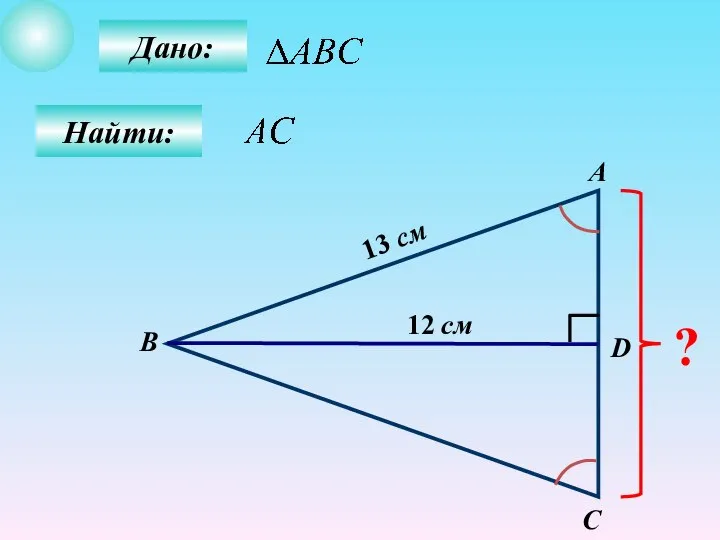
- 12. Дано: Найти: А B C D ? 12 см 13 см
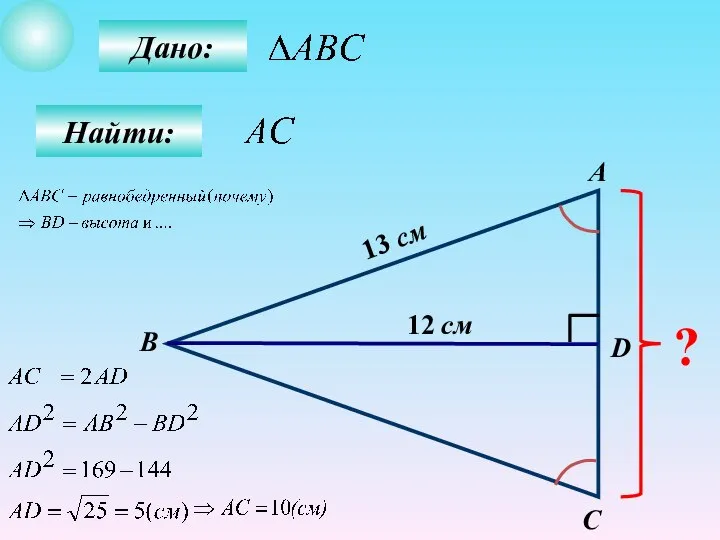
- 13. Дано: Найти: А B C D ? 12 см 13 см
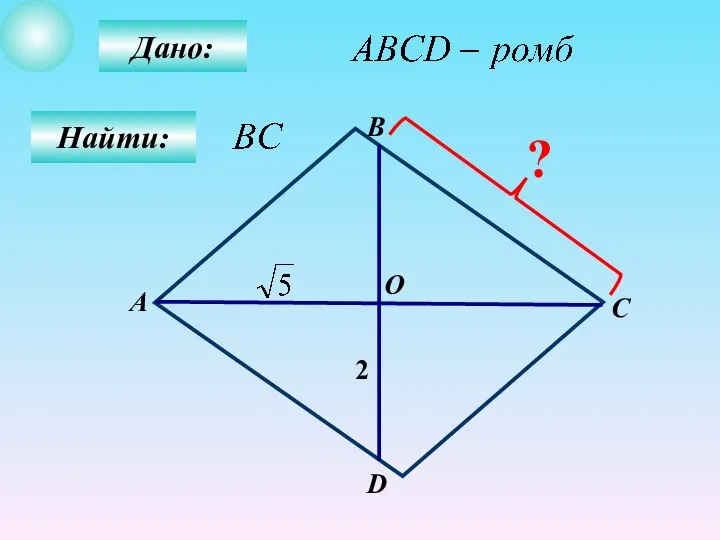
- 14. Дано: Найти: В А С О D 2 ?
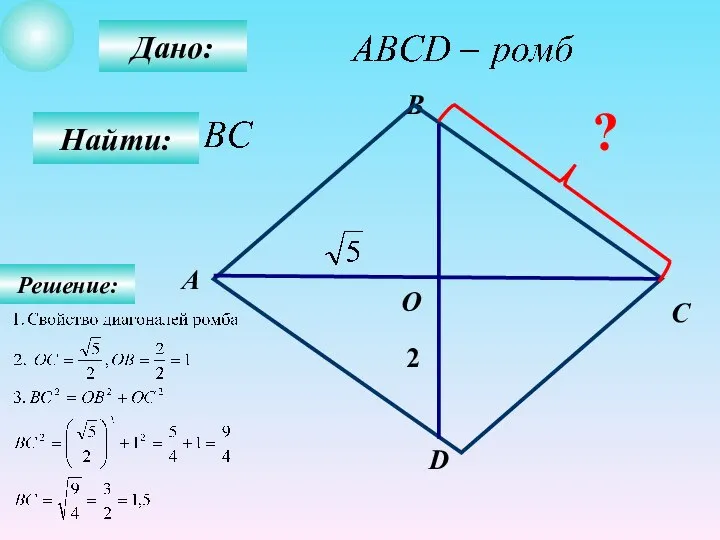
- 15. Дано: Найти: В А С О D 2 ? Решение:
- 16. Первый признак подобия треугольников
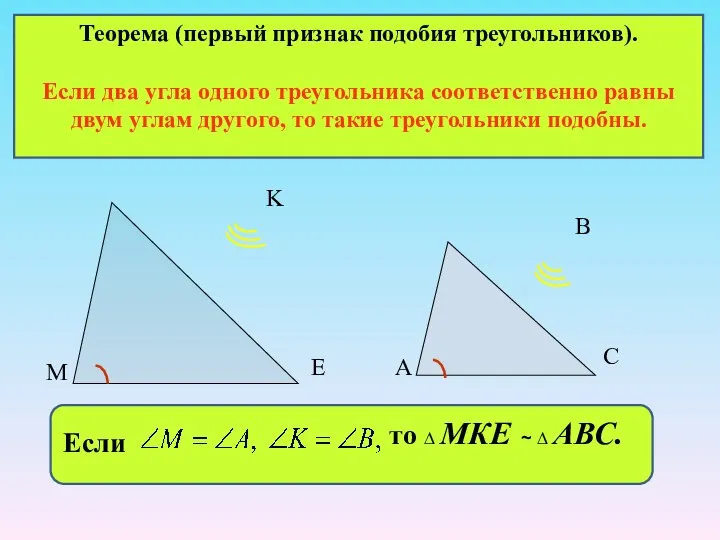
- 17. Теорема (первый признак подобия треугольников). Если два угла одного треугольника соответственно равны двум углам другого, то
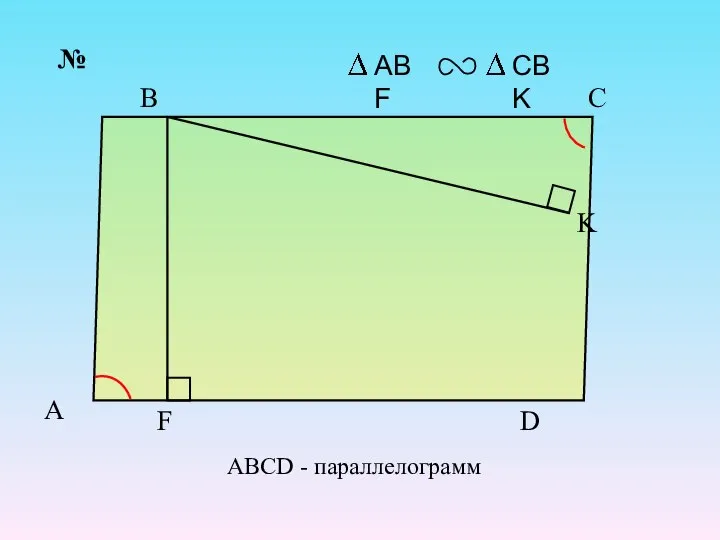
- 18. A K F D C B № ABCD - параллелограмм
- 19. Второй признак подобия треугольников
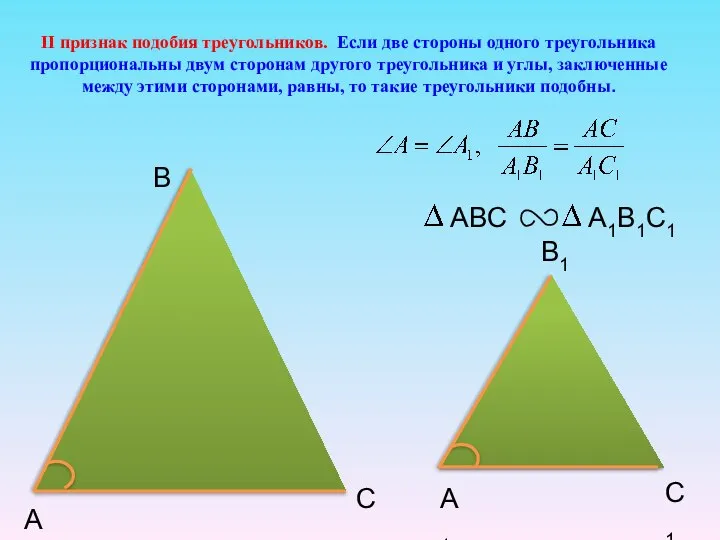
- 20. II признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы,
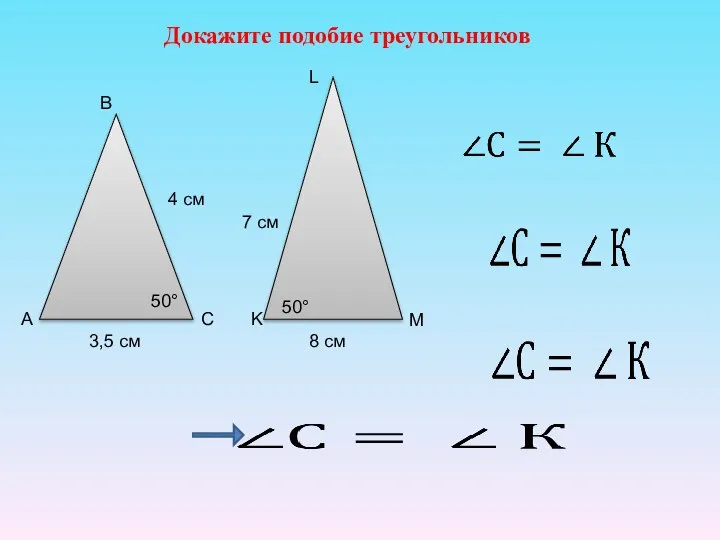
- 21. Докажите подобие треугольников А 3,5 см С В 4 см 50° K L M 7 см
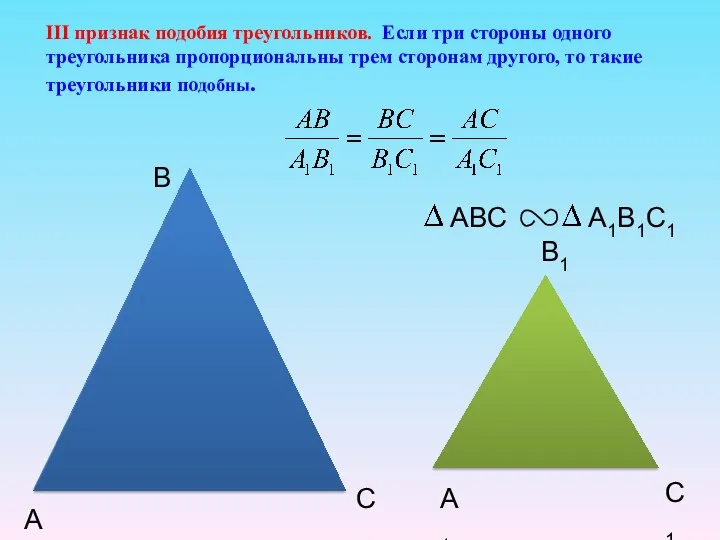
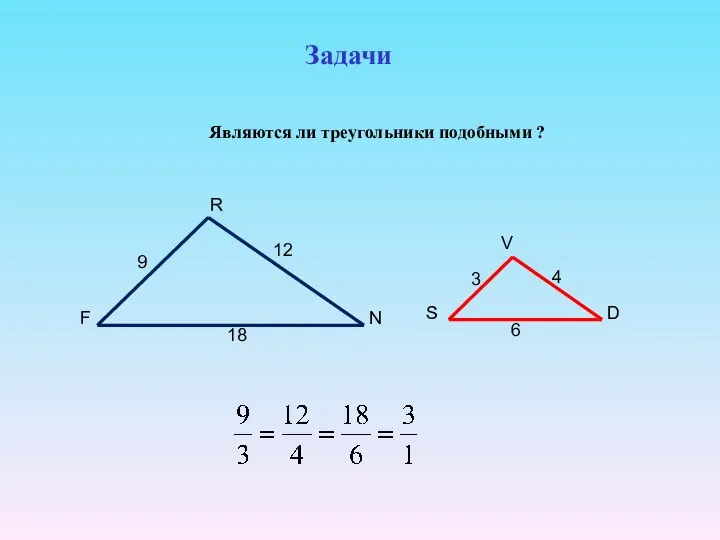
- 22. А B C А1 B1 C1 III признак подобия треугольников. Если три стороны одного треугольника пропорциональны
- 24. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ
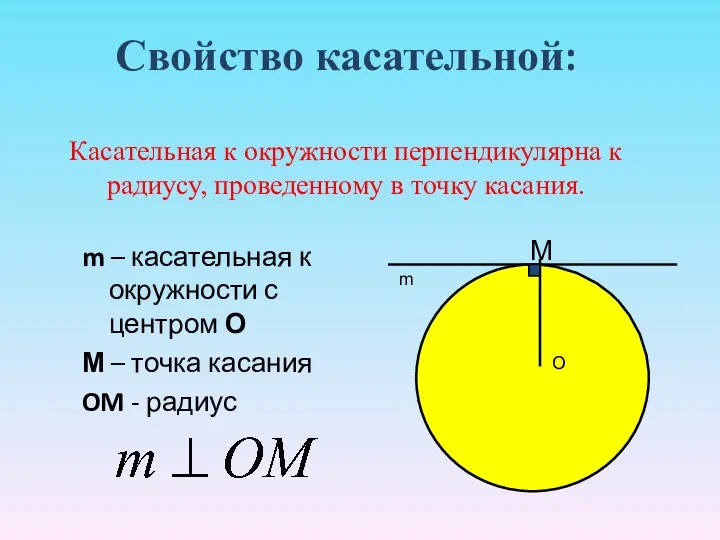
- 25. Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. m – касательная к
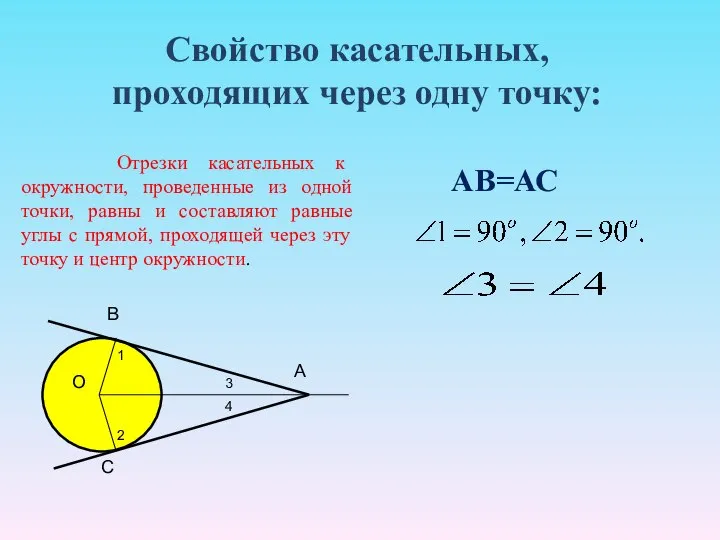
- 26. Свойство касательных, проходящих через одну точку: О В С А 1 2 3 4 Отрезки касательных
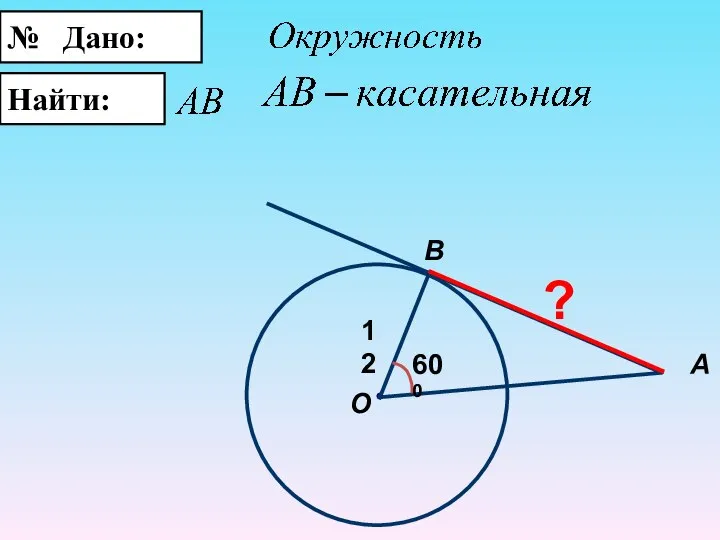
- 27. № Дано: Найти: B О А 12 600 ?
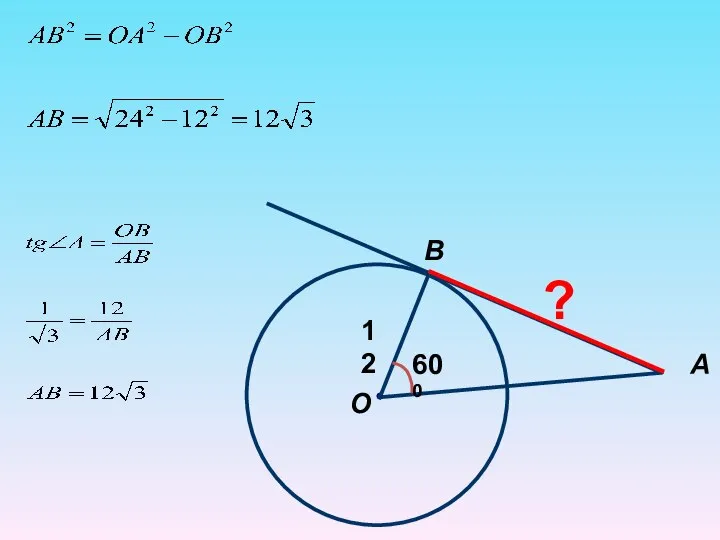
- 28. B О А 12 600 ?
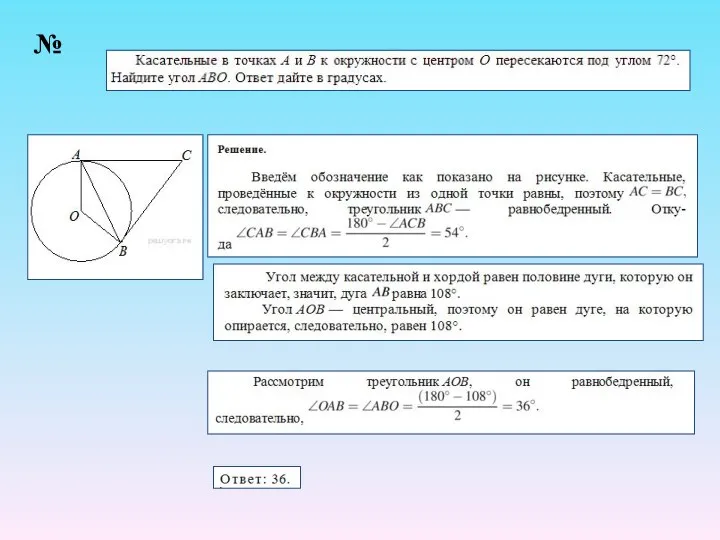
- 29. №
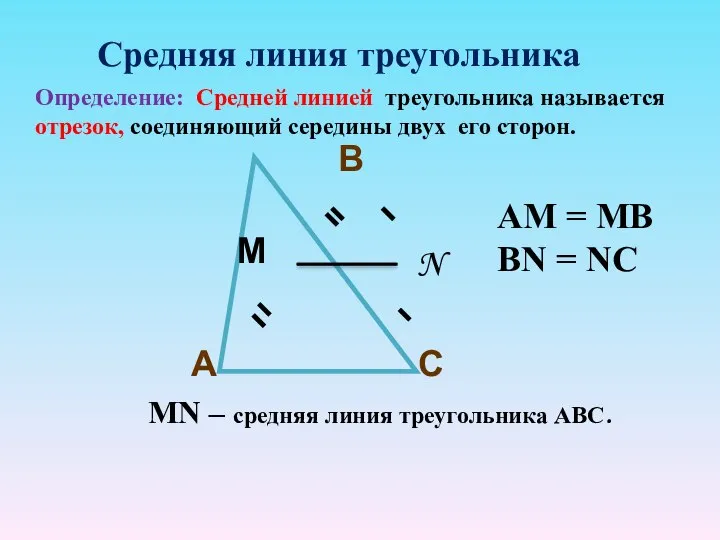
- 30. С В А М N МN – средняя линия треугольника АВС. Определение: Средней линией треугольника называется
- 31. Средняя линия равностороннего треугольника АВС равна 8 см. Найти периметр этого треугольника. А В С Р
- 32. Вариант 1. 1.Дано: ABCD – прямоугольник; ∠ABD=48°. Найти: ∠СОD, ∠СAD. 2.Угол ромба равен 32°. Найдите углы,
- 34. Скачать презентацию











 Прибавить и вычесть число 3. Решение текстовых задач
Прибавить и вычесть число 3. Решение текстовых задач Презентация на тему Золотое сечение - гармония математики
Презентация на тему Золотое сечение - гармония математики  Тренинговая работа №3
Тренинговая работа №3 Свойства числовых функций
Свойства числовых функций Логарифм числа и его свойства
Логарифм числа и его свойства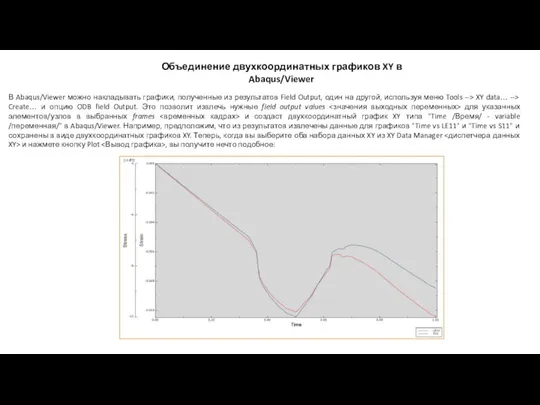 Объединение двухкоординатных графиков XY в Abaqus/Viewer
Объединение двухкоординатных графиков XY в Abaqus/Viewer Повторюємо арифметичні дії множення і ділення
Повторюємо арифметичні дії множення і ділення Устный счёт
Устный счёт Առարկա՝ Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում (ընտրովի դասընթաց)
Առարկա՝ Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում (ընտրովի դասընթաց) Уравнения с параметром
Уравнения с параметром Действия со смешанными числами
Действия со смешанными числами Разбор типового расчета по статистике
Разбор типового расчета по статистике Путешествие в страну дроби
Путешествие в страну дроби Геометрический калейдоскоп
Геометрический калейдоскоп Математическая игра Счастливое число 7!
Математическая игра Счастливое число 7! Интегральное исчисление
Интегральное исчисление Методика обучения математике и ее предмет
Методика обучения математике и ее предмет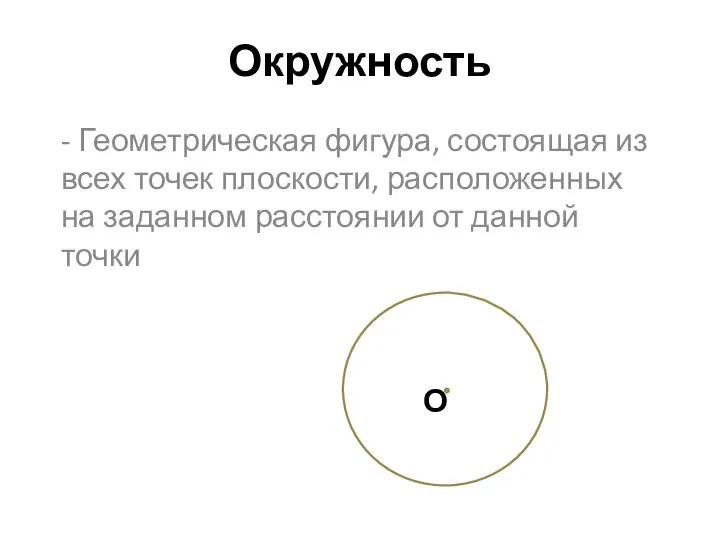 Окружность. Элементы окружности
Окружность. Элементы окружности Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Логические задачи. 1 класс
Логические задачи. 1 класс Движение. Виды движения
Движение. Виды движения Дидактическая игра. Веселый ёжик
Дидактическая игра. Веселый ёжик Násobíme a delíme s Mimoňmi
Násobíme a delíme s Mimoňmi Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Пересечение поверхностей
Пересечение поверхностей Презентация на тему Таблицы истинности
Презентация на тему Таблицы истинности  Дискретная математика с элементами математической логики. Основы теории множеств
Дискретная математика с элементами математической логики. Основы теории множеств Викторина по математике, 1 класс
Викторина по математике, 1 класс