Содержание
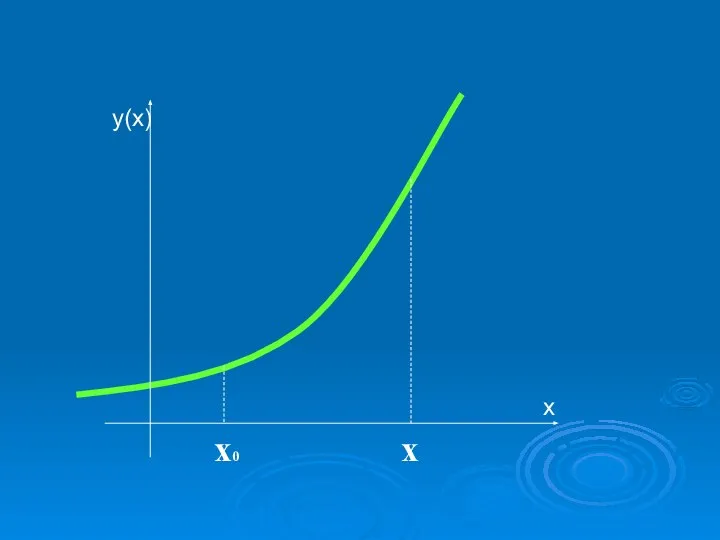
- 2. х0 х
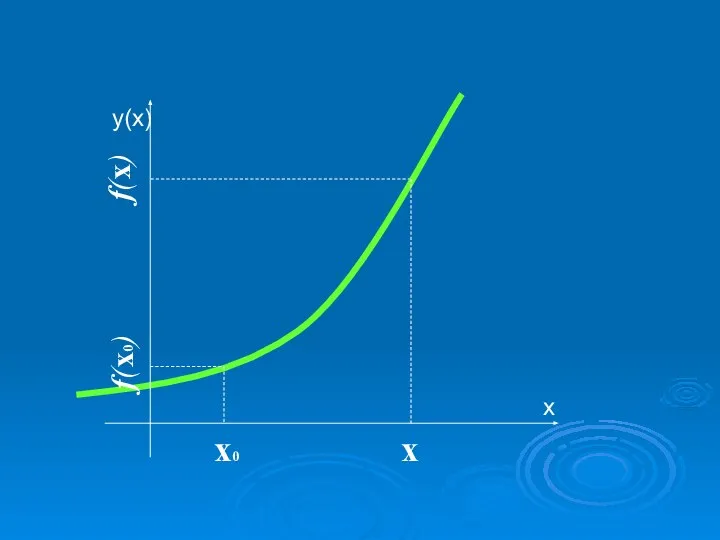
- 3. х0 х f(x0) f(x)
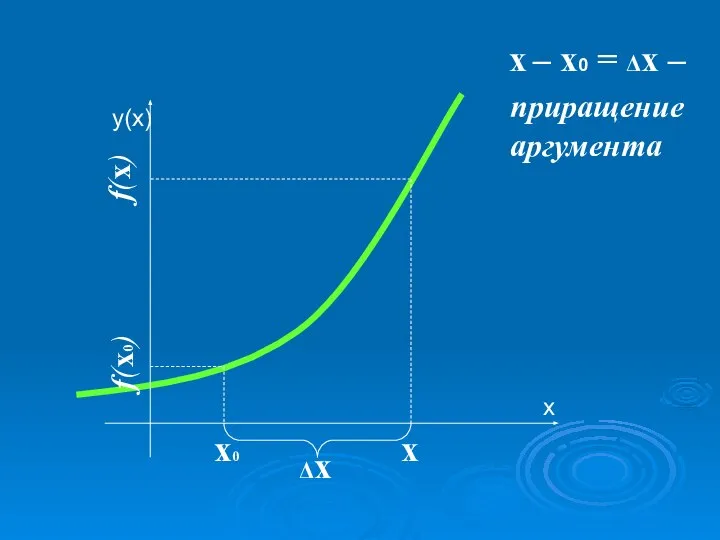
- 4. х0 х х – х0 = Δх – Δх f(x) f(x0) приращение аргумента
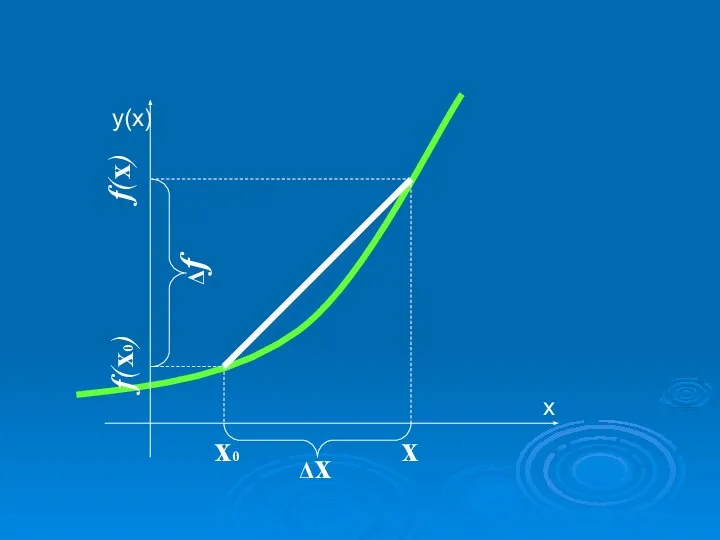
- 5. х0 х Δх f(x) f(x0) Δf
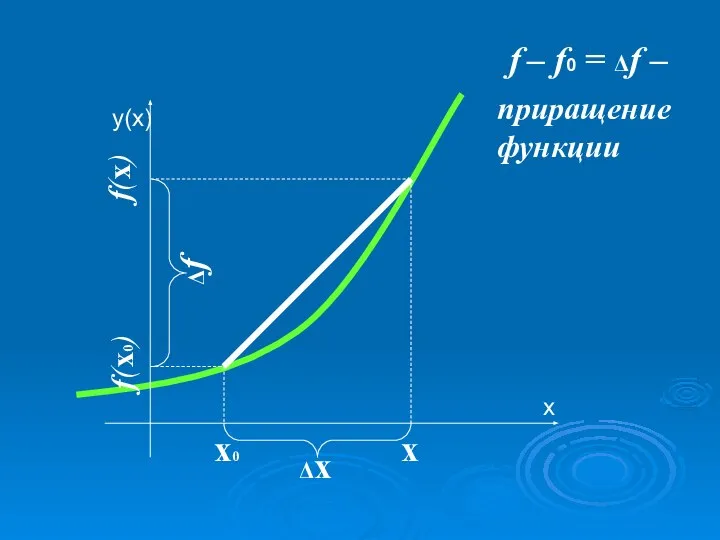
- 6. х0 х Δх f(x) f(x0) Δf f – f0 = Δf – приращение функции
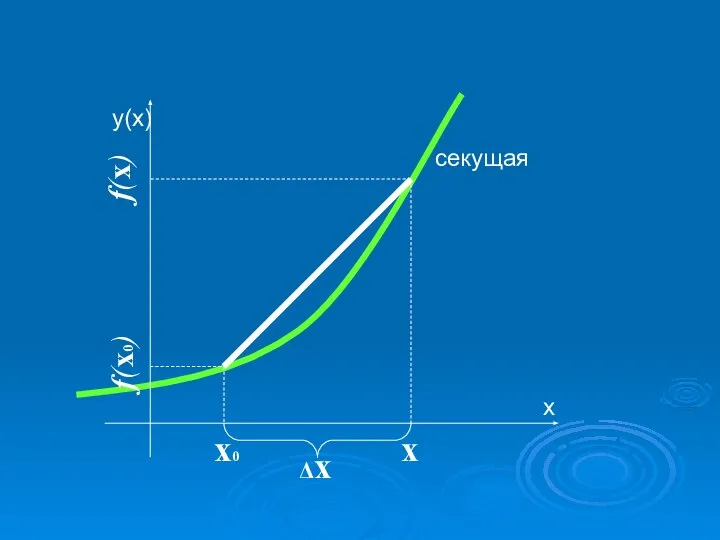
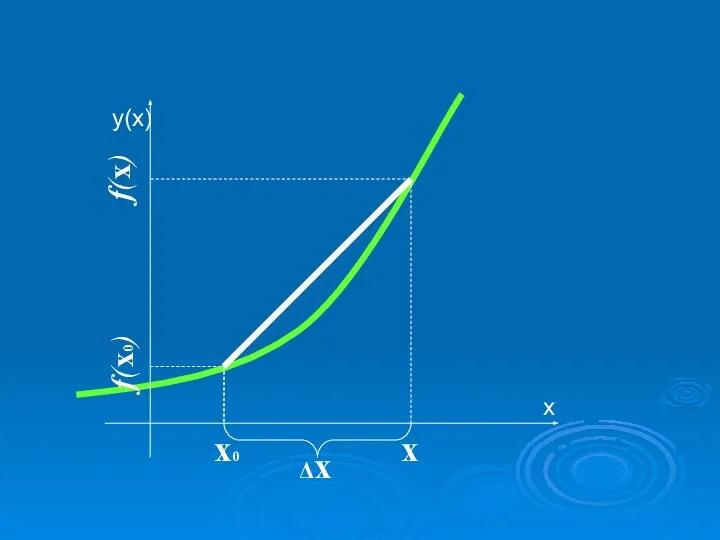
- 7. х0 х Δх f(x) f(x0) секущая
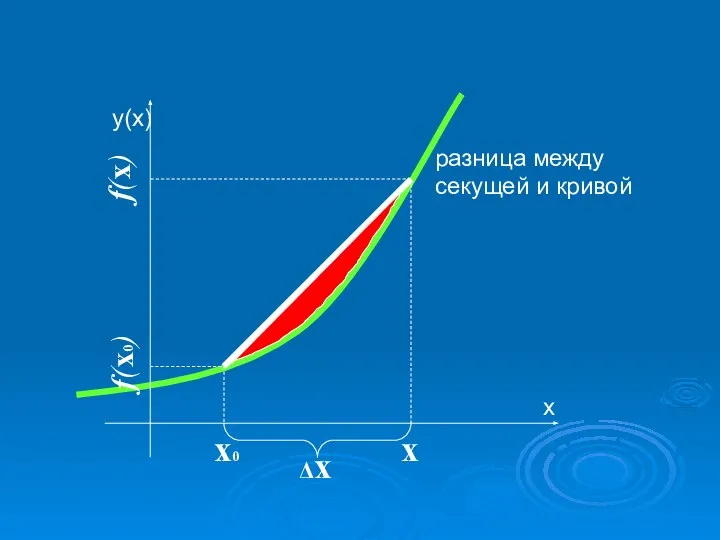
- 8. х0 х Δх f(x) f(x0) разница между секущей и кривой
- 9. f(x) f(x0)
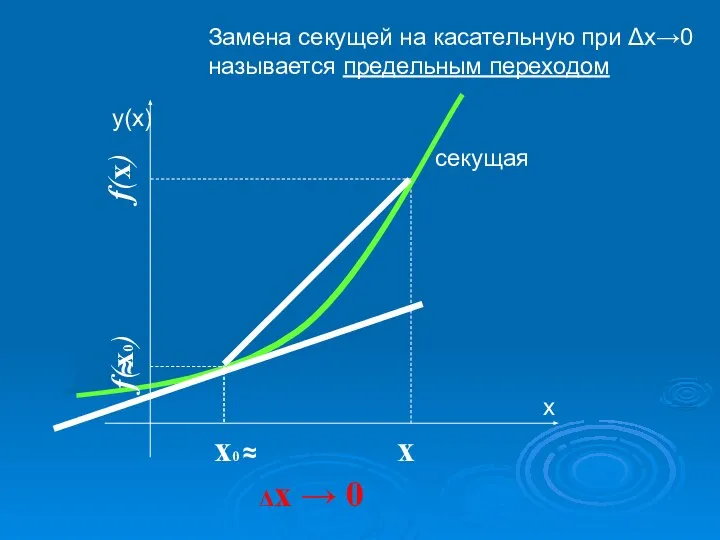
- 10. х0 х Δх → 0 секущая ≈ f(x0) ≈ f(x) Замена секущей на касательную при Δх→0
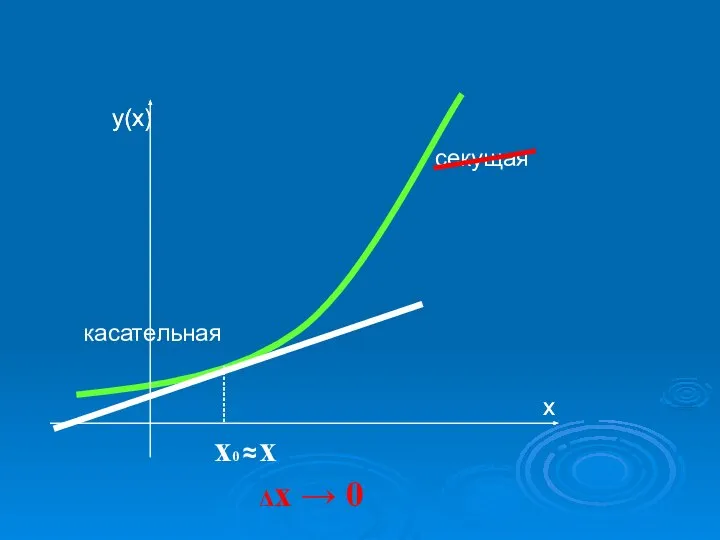
- 11. х0 х Δх → 0 секущая ≈ касательная
- 12. Выводы: Кривые в каждой своей точке меняют угол наклона; Для построения кривой нужно знать бесконечное множество
- 13. Связь между касательной и кривой (графиком функции) График функции f (х)≠ Новая производная функция f '(х)=
- 14. Определение производной Производной функции f '(х) называется предел отношения приращения функции к приращению аргумента при Δх→0
- 16. Скачать презентацию



 Статистика. Занятие 5
Статистика. Занятие 5 Презентация на тему Определение степени с натуральным показателем
Презентация на тему Определение степени с натуральным показателем  Практикум 2
Практикум 2 Решение экстремальных задач с помощью первой производной
Решение экстремальных задач с помощью первой производной Окружность и круг
Окружность и круг Моделирование. Объекты и их модели. (Тема 10)
Моделирование. Объекты и их модели. (Тема 10) Понятия и виды средних величин. Показатели вариации. Тема: 6.1
Понятия и виды средних величин. Показатели вариации. Тема: 6.1 Формула Бернулли
Формула Бернулли Свойства логарифмов
Свойства логарифмов Расчет параметров слоев
Расчет параметров слоев Взаимное расположение двух окружностей
Взаимное расположение двух окружностей Перпендикулярные прямые
Перпендикулярные прямые Функциональное зонирование
Функциональное зонирование Второй признак равенства треугольников
Второй признак равенства треугольников Презентация на тему Виды многогранников
Презентация на тему Виды многогранников  Умножение натуральных чисел
Умножение натуральных чисел Луч. Отрезок
Луч. Отрезок Исследование функции при помощи производной
Исследование функции при помощи производной Теорема Пифагора
Теорема Пифагора Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные
Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов Решение уравнений, содержащих переменную под знаком модуля
Решение уравнений, содержащих переменную под знаком модуля Параллельные прямые
Параллельные прямые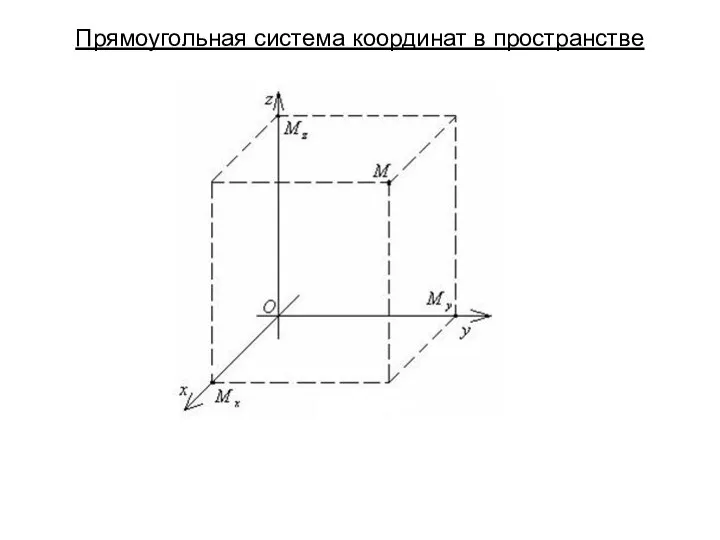 Прямоугольная система координат в пространстве. Понятие вектора
Прямоугольная система координат в пространстве. Понятие вектора Арккосинус, арксинус, арктангенс и арккотангенс
Арккосинус, арксинус, арктангенс и арккотангенс Перпендикуляр и наклонная к прямой
Перпендикуляр и наклонная к прямой Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Задачи на построение
Задачи на построение