Как называется отрезок AM?

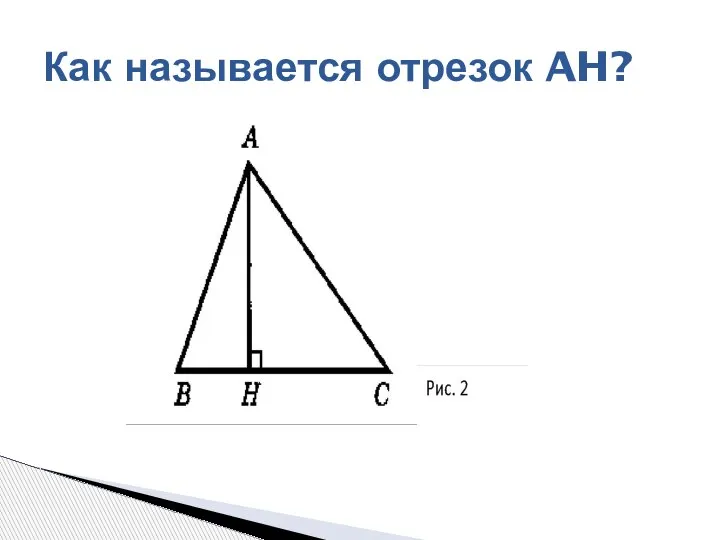
Как называется отрезок AH?

«Равнобедренный треугольник и его свойства»
Тема урока:

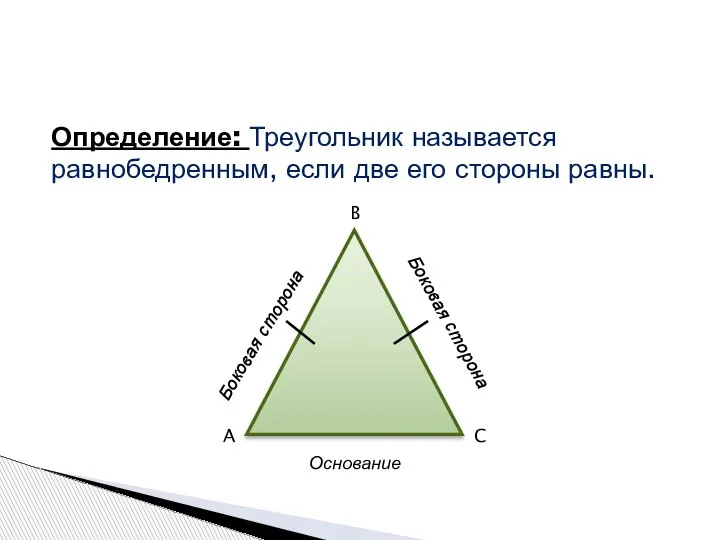
Определение: Треугольник называется равнобедренным, если две его стороны равны.
A
B
C
Боковая сторона
Боковая сторона
Основание

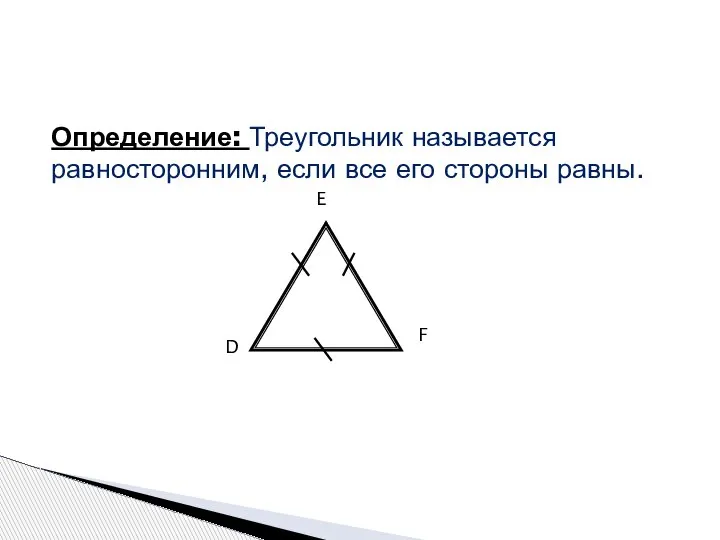
Определение: Треугольник называется равносторонним, если все его стороны равны.
D
E
F

Свойства равнобедренного треугольника
B
A
C

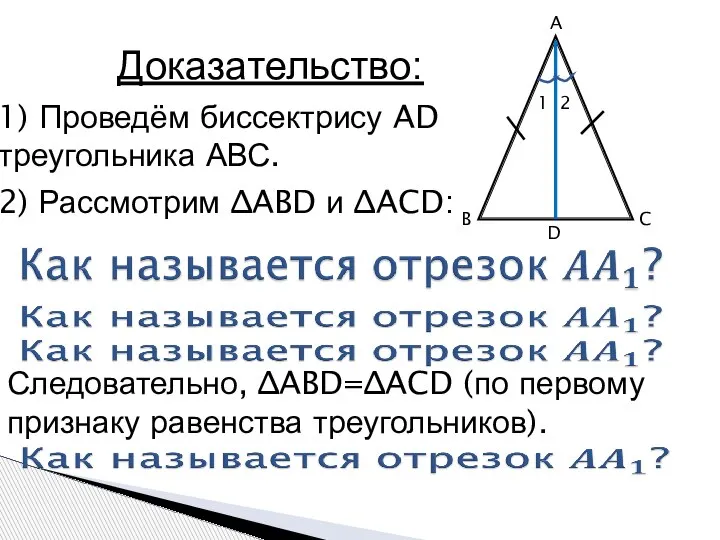
A
B
C
D
Доказательство:
1) Проведём биссектрису AD треугольника АВС.
2) Рассмотрим ∆ABD и ∆ACD:
1
2
Следовательно, ∆ABD=∆ACD (по первому признаку равенства треугольников).

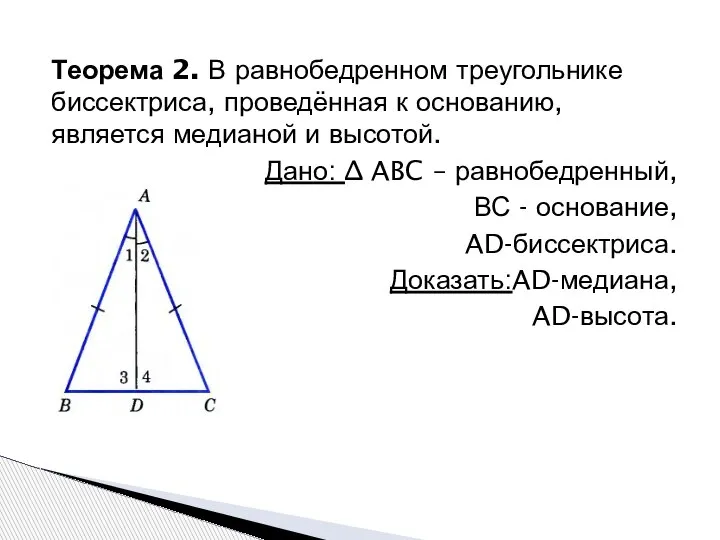
Теорема 2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Дано: ∆ ABC – равнобедренный,
ВС - основание,
AD-биссектриса.
Доказать:AD-медиана,
AD-высота.

Доказательство:
1) Рассмотрим ∆ABD и ∆ACD:
Следовательно, ∆ABD=∆ACD (по первому признаку равенства треугольников).

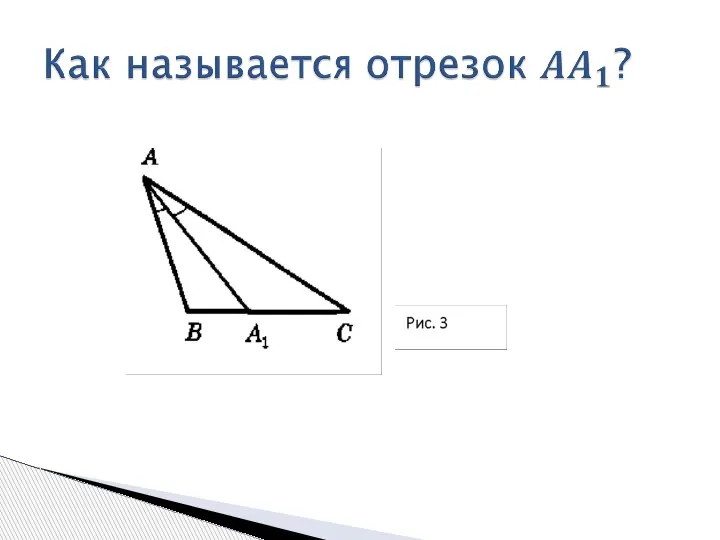
1. Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.
2. Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.

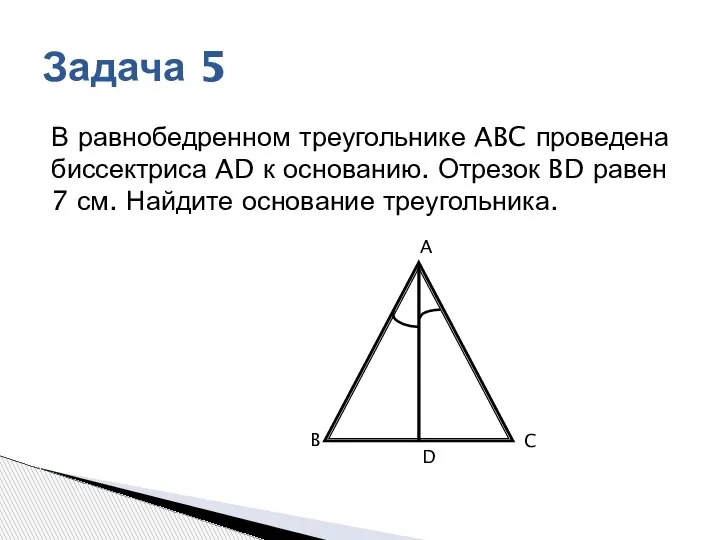
A
B
C
Задача 4

В равнобедренном треугольнике ABC проведена биссектриса AD к основанию. Отрезок BD равен 7 см. Найдите основание треугольника.
Задача 5
A
B
C
D