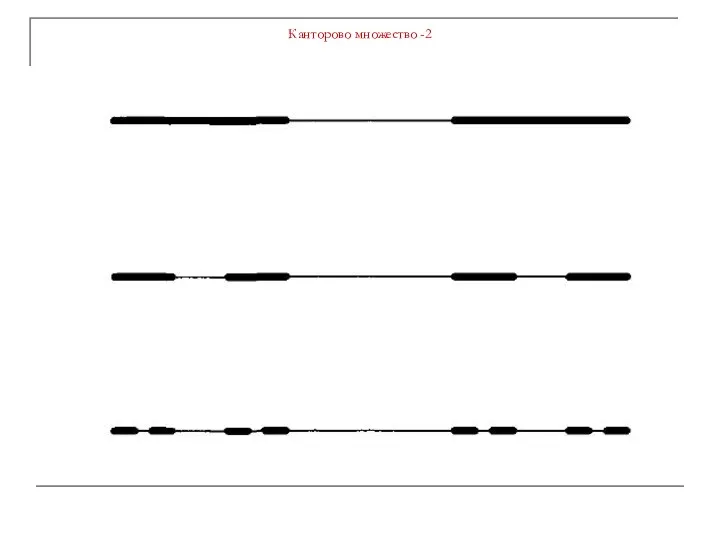
Слайд 2Канторово множество -1
0) Отрезок I = [0; 1].
1) Делим I на три
![Канторово множество -1 0) Отрезок I = [0; 1]. 1) Делим I](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1128171/slide-1.jpg)
равных отрезка:
Средний интервал удаляем. Остаются
2) С каждым из двух оставшихся отрезков делаем то же.
А именно, получаем 6 отрезков длиной 1/9 и
из которых удаляем средние интервалы. Остаются .
3) С каждым из четырех оставшихся отрезков делаем то же.
И Т. Д.
Слайд 4Канторово множество -3
Сумма длин удаленных интервалов:
Получается, что из отрезка длиной 1 удалили

интервалы, сумма длин которых также равна 1. А что-нибудь осталось?
Да, и осталось «столько же» точек, сколько было на [0;1].
Кодировка точек канторовского множества.
Пусть любая послед-ть символов 0 и 2. Тогда
послед-ть стягивающихся отрезков, у которых есть ровно одна общая точка .
Слайд 5Канторово множество -4
Примеры.
Точка: 0 Код: (000…..)
Точка: 1 Код: (222…..)
Точка:

1/3 Код: (0222…..)
Точка: 7/9 Код: (20222…..)
Код: (2202000….) Точка:
Код: (20202020(20)) Точка:
Код: . Точка:
Точки 1-го рода - в коде есть «хвост» из 0 или «хвост» из 2, т.е. концы удаляемых интервалов. Точки 2-го рода – остальные.
Слайд 6Канторово множество -5
Ф 1.К континуально(=существует биекция между К и [0;1] ).
До-во.
К
![Канторово множество -5 Ф 1.К континуально(=существует биекция между К и [0;1] ).](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1128171/slide-5.jpg)
биективно множеству всех последовательностей из двух символов 0 и 2,
которое биективно множеству всех подмножеств множества натуральных чисел,
которое континуально ( ).
Слайд 8Ф 2. Существует сюръекция s из К на [0;1]
Док-во.
Возьмем точку из
![Ф 2. Существует сюръекция s из К на [0;1] Док-во. Возьмем точку](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1128171/slide-7.jpg)
К. Выпишем ее код из 0 и 2. Все 2 заменим на 1. Получим последовательность из 0 и 1.
Рассмотрим ее как разложение действительного числа из [0;1] в бесконечную двоичную дробь. Всё.
Слайд 9Канторово множество -6
Ф 3 = Ф 1. К континуально
Док-во.
Значит, К и

[0;1] биективны подмножествам друг друга.
Остается сослаться на теорему Кантора-Бернштейна-Шрёдера.
Ф 4. Сюръекция - не иньекция.
Док-во.
Всегда для любого удаляемого интервала
Слайд 10Канторово множество - 7
Ф 5. Сюръекция непрерывна.
Док-во. Формальный ответ:
Неформально. Если коды

двух точек
x и y совпали на первых n местах, то и тогда
двоичные дроби s(x),s(y) совпали на первых n местах, т.е.
Остается формализовать переход
Слайд 11Канторово множество - 8
Ф 6 (Канторова лестница, «чортова» лестница). Существует непрерывная неубывающая

сюръекция отрезка на себя, которая почти всюду постоянна.
Док-во.
Продолжим сюръекцию на интервалы, удаляемые в процессе построения множества К самым простым образом.
А именно, так как всегда для любого удаляемого интервала , то на этом интервале наша функция будет соответствующей константой.
Слайд 12
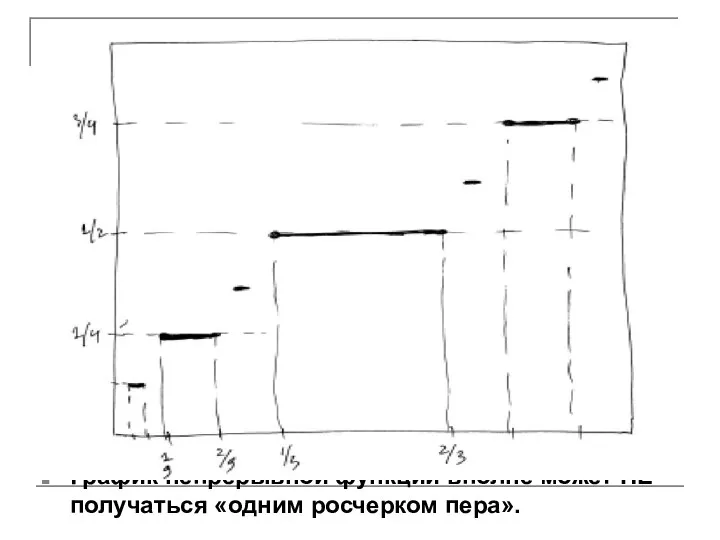
График непрерывной функции вполне может НЕ получаться «одним росчерком пера».
Слайд 14Канторово множество - 9
Ф 7. К - компакт без изолированных точек.
Ф

8. К нигде не плотно (= в любом интервале есть подинтервал, в котором нет точек из К).
Док-во.
Для интервала (a;b) выберем n так, чтобы .
Разделим [0;1] на одинаковых отрезков. Один из них, скажем , целиком лежит в (a;b) .
Если на n-ом шаге построения К внутренность удаляют, то - нужный подинтервал.
Если нет, то на следующем шаге удаляют среднюю треть
и эта треть - нужный подинтервал.
Слайд 15Канторово множество - 10
Ф 9. Если F - замкнутое подмножество К ,

то существует непрерывная сюръекция такая, что . (F – ретракт К).
Док-во.
Возьмем
По Ф8 найдем .
Вырежем из прямой и разрез максимально раздвинем:
отобразим в , а отобразим в
Слайд 16
Все точки из F, как и требуется, оставим на месте..
Теорема Мазуркевича. Замкнутое
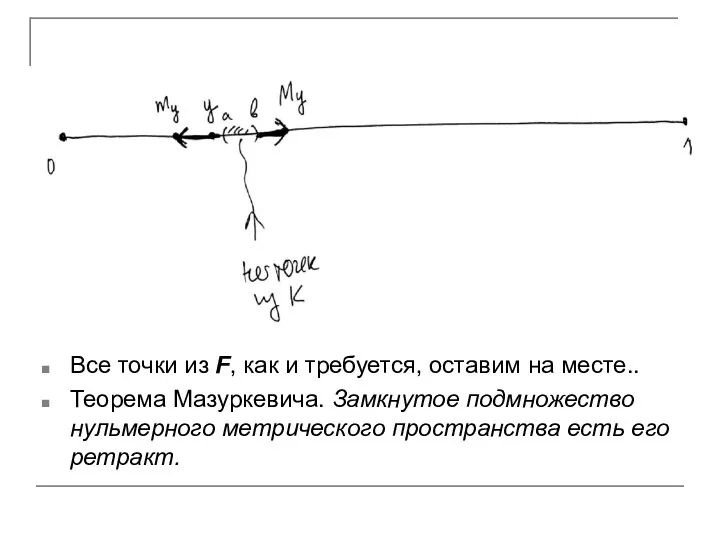
подмножество нульмерного метрического пространства есть его ретракт.
Слайд 17Канторово множество - 11
Ф 10. Для любого метрического компакта X существует непрерывная

сюръекция .
Док-во 1 (обходное).
1) Сначала Ф10 устанавливается для специального X, для гильбертова куба : .
2) Затем используется (иньективная) универсальность :
3) Пусть . Применяем Ф9 о ретракции:
4) Тогда -
то, что нужно:
Слайд 18Канторово множество - 12
Док-во 2 (почти прямое).
1) Для любого в метрическом компакте

X есть конечная сеть, т.е. конечное множество такое, что
2) Строим конечные сети для
3) Выписываем поочередно все сети друг за другом. Получаем последовательность плотную в X.
4) К каждой точке «привязан» открытый шарик
5) Пусть код точки .Определим
по правилу
6) Пересечение или пусто, или одноточечно.
7) Пусть F - множество тех точек из K, для которых непусто.
Оказывается, что F – замкнуто, а отображение
есть непрерывная сюръекция .
8) Остается использовать Ф9 о ретракции:
и определить
Слайд 19Mix
Ф11. К – нульмерен
(=в любой окрестности любой точки есть открыто-замкнутое подмножество

)
Ф12. (уникальность К)
Всякий нульмерный метрический компакт без изолированных точек гомеоморфен К.
Ф13. Существует непрерывная сюрьекция отрезка на любой выпуклый компакт Х.
: сюръекцию продолжить на смежные интервалы по линейности.
Слайд 20Mix
Ф14. К – однороден (=любую точку можно перевести в любую автогомеоморфизмом) и

строго однороден (=все clopen гомеоморфны).
Ф15. (частичное решение СН)
Несчетное замкнутое числовое множество содержит копию К и поэтому континуально.
Ф15’ Если непрерывно отображает полное метрическое пространство X на несчетное пространство Y , то X содержит копию К и поэтому неравенство невозможно.
Ф16. Существует измеримое, не борелевское множество.
![Канторово множество -1 0) Отрезок I = [0; 1]. 1) Делим I](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1128171/slide-1.jpg)


![Канторово множество -5 Ф 1.К континуально(=существует биекция между К и [0;1] ).](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1128171/slide-5.jpg)

![Ф 2. Существует сюръекция s из К на [0;1] Док-во. Возьмем точку](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1128171/slide-7.jpg)












 Ребусы по математике
Ребусы по математике Свойства степени с рациональным показателем
Свойства степени с рациональным показателем Устный счет
Устный счет Симметрия в пространстве
Симметрия в пространстве Бесконечность величин
Бесконечность величин Геометрический смысл производной. Решение примеров на геометрический смысл производной
Геометрический смысл производной. Решение примеров на геометрический смысл производной На лесной поляне
На лесной поляне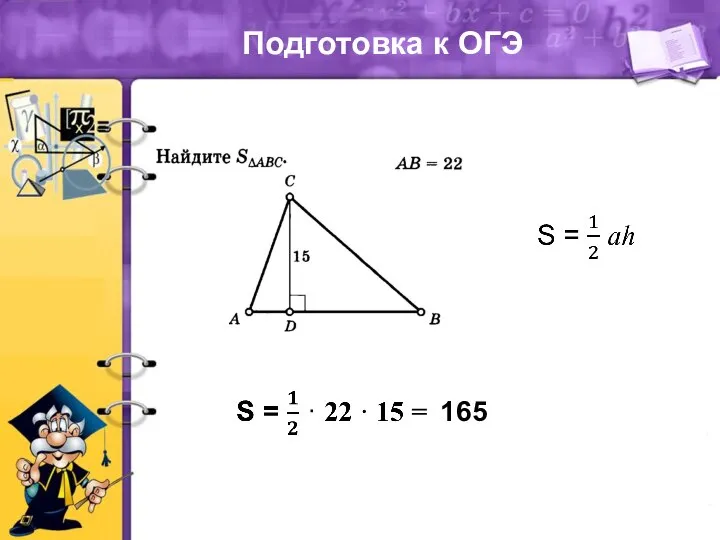 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Проект-игра по геометрии Занимательная геометрия
Проект-игра по геометрии Занимательная геометрия Решение задач на нахождение значений двух величин по сумме и разности
Решение задач на нахождение значений двух величин по сумме и разности Таблица умножения на 3 в стихах
Таблица умножения на 3 в стихах Диофантово уравнение
Диофантово уравнение Учить – значит удивлять
Учить – значит удивлять Задача на процкеты
Задача на процкеты Геометрические фигуры (открытый урок - игра Поле чудес)
Геометрические фигуры (открытый урок - игра Поле чудес) Понятие логарифма
Понятие логарифма Способ группировки
Способ группировки Метод линейного сплайна
Метод линейного сплайна Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс Готовимся к ОГЭ по математике
Готовимся к ОГЭ по математике Свойства умножения. 5 класс
Свойства умножения. 5 класс Дроби вокруг нас
Дроби вокруг нас Из истории теоремы Пифагора
Из истории теоремы Пифагора Решение задач на нахождение вероятности
Решение задач на нахождение вероятности Презентация на тему Дробные числа
Презентация на тему Дробные числа  Умножение и деление комплексных чисел
Умножение и деление комплексных чисел Алгебра в нашей жизни
Алгебра в нашей жизни Повторение и расширение сведений о функции
Повторение и расширение сведений о функции