Содержание
- 2. Пусть y=f(x)- заданная функция. График этой функции может быть подвергнут преобразованиям: y = f(x)+a y =
- 3. Заметим, что в уравнении функции y = f(x)+a «а»- слагаемое при f(x). Значит: при одном значении
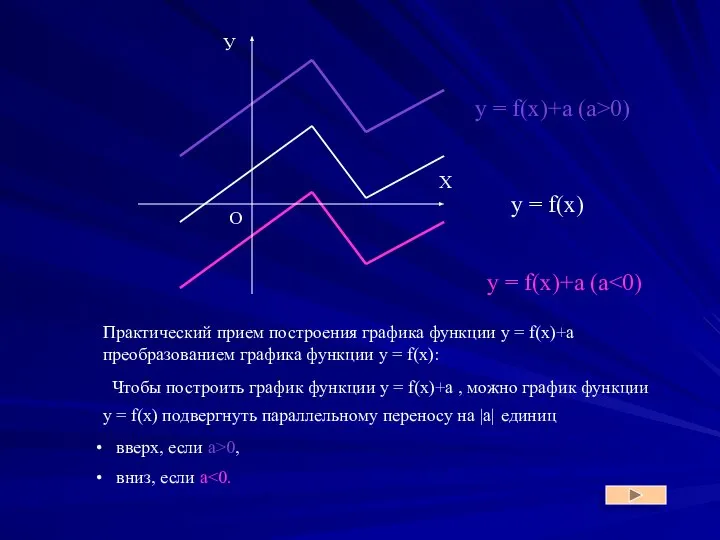
- 4. Практический прием построения графика функции y = f(x)+a преобразованием графика функции y = f(x): Чтобы построить
- 5. Возврат Элементы самоконтроля (правильности построения графика): Аналитическим путем найти область определения функции и сопоставить с соответствующим
- 6. Преобразование y=f(x+a) 1. Сравнивая уравнения функций y = f(x) и y = f(x+a), заметим, что «a»
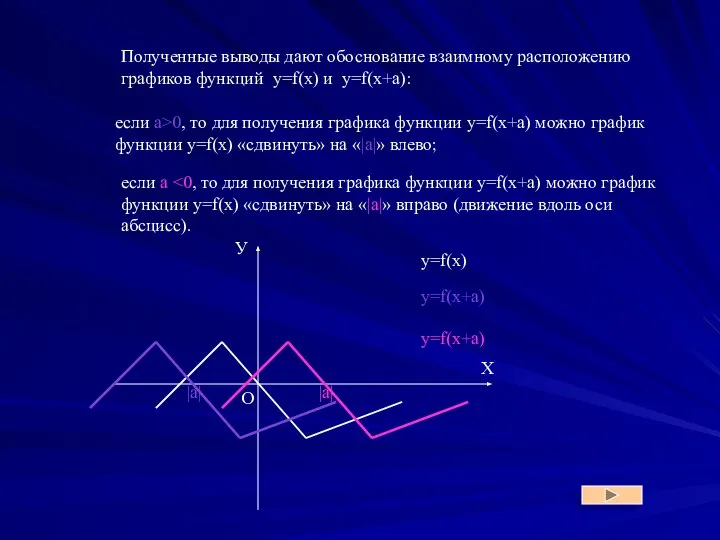
- 7. Полученные выводы дают обоснование взаимному расположению графиков функций y=f(x) и y=f(x+a): если а>0, то для получения
- 8. Преобразование y=-f(x) Уравнение функции y = - f(x) можно привести к виду y = (-1)f(x). Не
- 9. При выполнении симметрии относительно оси абсцисс целесообразно помнить: отрезки переходят в равные отрезки, прямые – в
- 10. Преобразование y=f(-x) 1. Чтобы установить взаимное расположение графиков выделенных функций, выясним взаимосвязь аргументов этих функций при
- 11. Геометрической интерпретацией полученного вывода является утверждение: если точка с координатами (х0,y0) – точка графика y=f(x), то
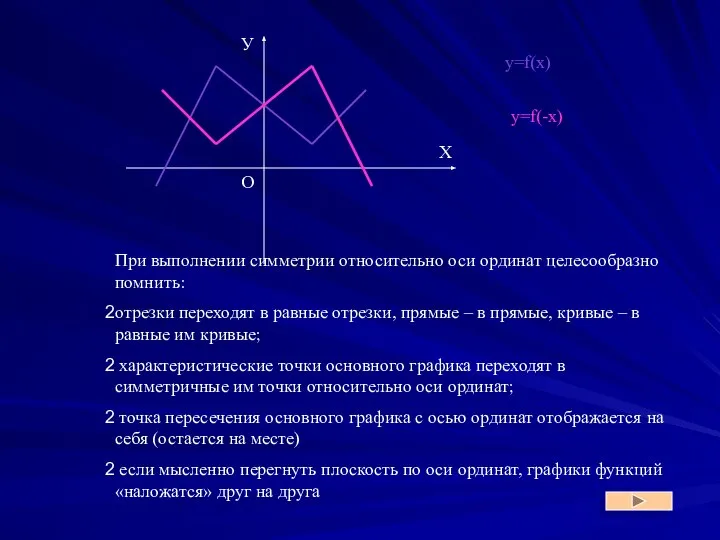
- 12. При выполнении симметрии относительно оси ординат целесообразно помнить: отрезки переходят в равные отрезки, прямые – в
- 13. Преобразование y=|f(x)| Значит, для построения графика функции y=|f(x)|, можно в одной системе координат построить графики функций
- 14. y=f(x) y=- f(x) Результатирующий график y=|f(x)| Практический прием: Для построения графика функции y=|f(x)| преобразованием графика y=f(x)
- 15. Преобразование y=f(|x|) Уравнение функции y=f(|x|) можно записать в виде: y= f(x), если x ≥ 0 f(-x),
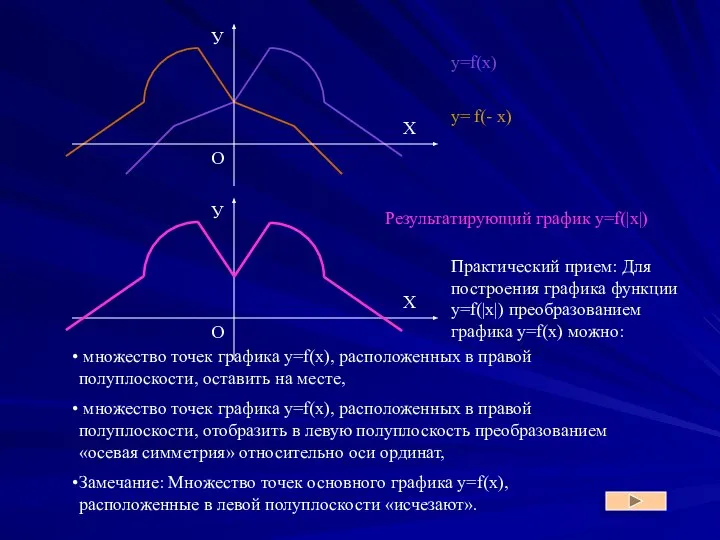
- 16. y=f(x) y= f(- x) Результатирующий график y=f(|x|) Практический прием: Для построения графика функции y=f(|x|) преобразованием графика
- 17. Преобразование у=af(x) Преобразование у=af(x) рассмотрим при а>0, выделяя случаи: 0 1. Замечание: Если а 0. Заметим,
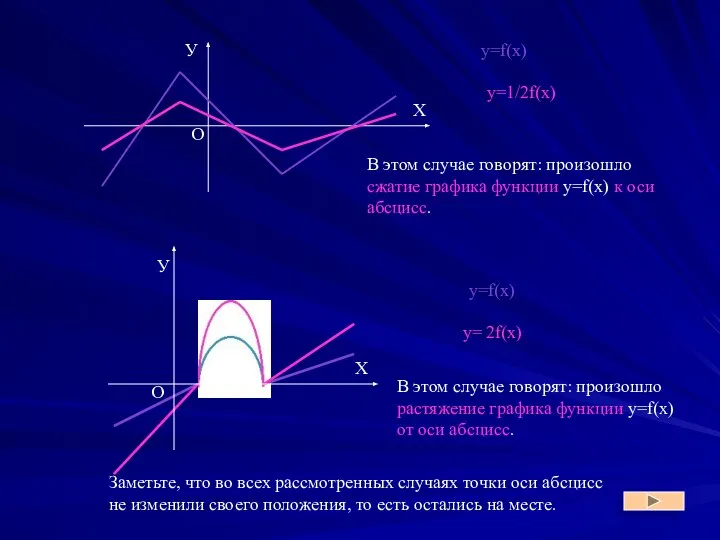
- 18. y=f(x) y=f(x) y=1/2f(x) y= 2f(x) В этом случае говорят: произошло сжатие графика функции y=f(x) к оси
- 19. Преобразование y=f(ax) Преобразование у=f(аx) рассмотрим при а>0, выделяя случаи: 0 1. Замечание: Если а 0. Чтобы
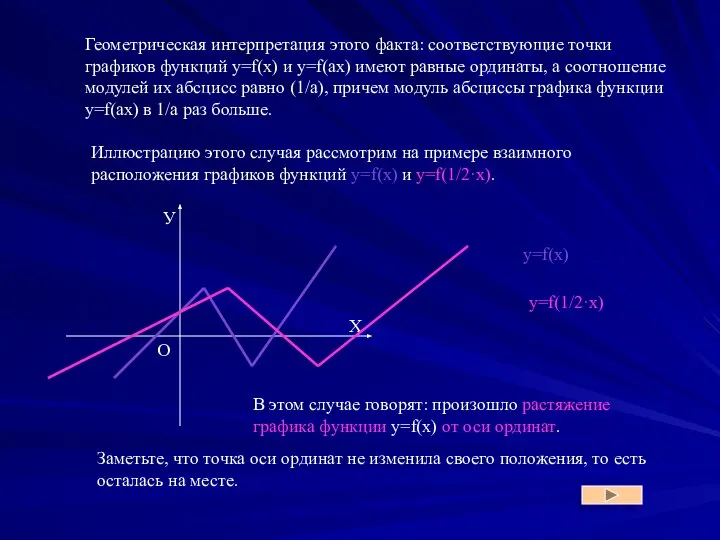
- 20. Геометрическая интерпретация этого факта: соответствующие точки графиков функций y=f(x) и у=f(аx) имеют равные ординаты, а соотношение
- 21. 2. Если а>1, то (1/а ) Геометрическая интерпретация этого факта: соответствующие точки графиков функций y=f(x) и
- 22. Комбинации преобразований y=f(x) y=|f(x)| Преобразование y=f(|x|) y=f(|x|) у=af(x) Преобразование у=af(x) y=f(ax) Преобразование y=f(ax)
- 27. Скачать презентацию


















 Сложение и вычитание дробей с одинаковыми знаменателями. Решение уравнений
Сложение и вычитание дробей с одинаковыми знаменателями. Решение уравнений Правила деления. (6 класс)
Правила деления. (6 класс) Векторы. 9 класс
Векторы. 9 класс Вторая производная и её физический смысл
Вторая производная и её физический смысл Повторение. Дроби
Повторение. Дроби Презентация на тему Арифметическая прогрессия в древности
Презентация на тему Арифметическая прогрессия в древности  Математический дизайн
Математический дизайн Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Основы моделирования
Основы моделирования Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика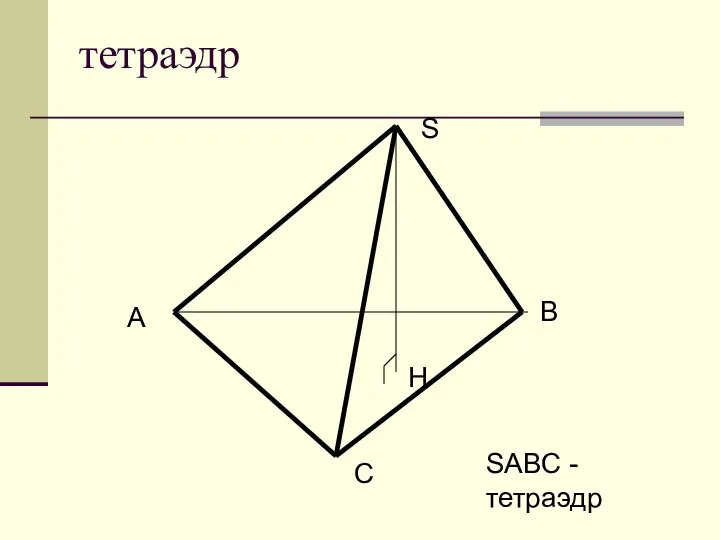 Тетраэдр
Тетраэдр Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда ОДУ высших порядков
ОДУ высших порядков Арифметический квадратный корень. Самостоятельная работа
Арифметический квадратный корень. Самостоятельная работа Признаки равенства треугольников. Подготовка к контрольной работе
Признаки равенства треугольников. Подготовка к контрольной работе Презентация на тему Вычитание и сказка "Царевна-лягушка" 2 класс
Презентация на тему Вычитание и сказка "Царевна-лягушка" 2 класс  Вычисление значений числовых выражений с действиями разной степени. Проверка деления умножением
Вычисление значений числовых выражений с действиями разной степени. Проверка деления умножением ВПР - 7- 9 класс
ВПР - 7- 9 класс Математика в биологии
Математика в биологии Уравнение вида ах2 + bx + c = 0,
Уравнение вида ах2 + bx + c = 0, Прямоугольный треугольник. Задачи. 7 класс
Прямоугольный треугольник. Задачи. 7 класс Историческая задача
Историческая задача Биометрия, как наука
Биометрия, как наука Решение задач (2 класс)
Решение задач (2 класс) Решение квадратных уравнений содержащих параметры в 9 классе
Решение квадратных уравнений содержащих параметры в 9 классе Презентация на тему Сложение дробей с одинаковыми знаменателями (5 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (5 класс)  Контрольная работа. Геометрия
Контрольная работа. Геометрия