достоверным или случайным.
а) Из 25 учащихся класса двое справляют день рождения 30 января.
б) Из 25 учащихся класса двое справляют день рождения 30 февраля.
в) Измерены длины сторон треугольника. Оказалось, что длина каждой стороны меньше суммы длин двух других сторон.
г) Бросают две игральные кости, сумма выпавших на двух костях очков меньше 15.
д) Бросают четыре игральные кости, на всех четырех костях выпало по 3 очка.
е) На уроке математики ученики решали математические задачи.
ж) Из интервала (1; 2) наугад взяли какое-то число, оно оказалось натуральным.
(Случайное.)
(Невозможное.)
(Достоверное.)
(Достоверное.)
(Случайное.)
(Достоверное.)
(Невозможное.)











 Неопределенный интеграл
Неопределенный интеграл Параллелограмм и трапеция. Урок 8
Параллелограмм и трапеция. Урок 8 Геометрические фигуры
Геометрические фигуры Предел последовательности. Урок 1
Предел последовательности. Урок 1 Презентация на тему Десятичные дроби
Презентация на тему Десятичные дроби  Колесо истории математики
Колесо истории математики Стародубцева Анна 9-а класс
Стародубцева Анна 9-а класс Бой эрудитов
Бой эрудитов Математические ребусы. 4 класс
Математические ребусы. 4 класс Понятие квадратного корня из неотрицательного числа
Понятие квадратного корня из неотрицательного числа Лето в цифрах. Маршрут поездки
Лето в цифрах. Маршрут поездки Разбиение множеств на классы
Разбиение множеств на классы Сложение десятичных дробей
Сложение десятичных дробей Число и цифра 1. 1 класс
Число и цифра 1. 1 класс Урок математики в 4 классе по системе Л.В.Занкова (1-4) «Действия с многозначными числами» Автор: Каграманян Елена Владимировна, учи
Урок математики в 4 классе по системе Л.В.Занкова (1-4) «Действия с многозначными числами» Автор: Каграманян Елена Владимировна, учи Классы интегрируемых функций
Классы интегрируемых функций Понятия возрастающей и убывающей функций. Понятие монотонности функции. Возрастание и убывание функции
Понятия возрастающей и убывающей функций. Понятие монотонности функции. Возрастание и убывание функции Приложения производной
Приложения производной Презентация на тему Свойства функции
Презентация на тему Свойства функции  Волшебная страна - Геометрия. Занятие 3
Волшебная страна - Геометрия. Занятие 3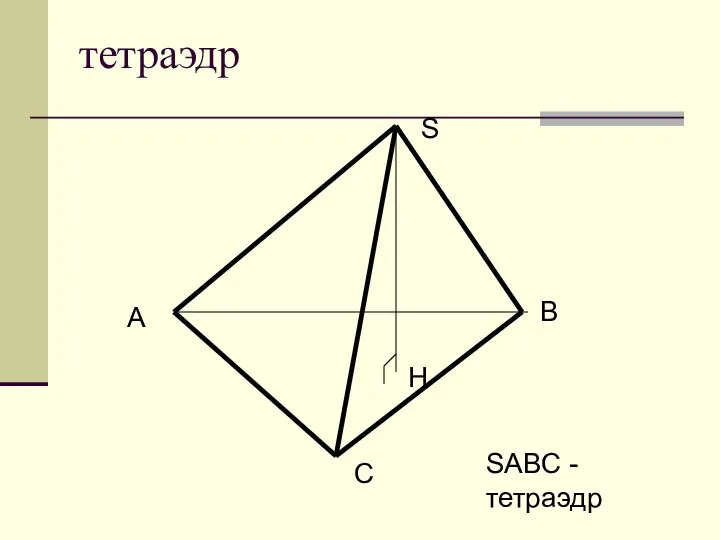 Тетраэдр
Тетраэдр Линейные рекуррентные соотношения и методы их решения
Линейные рекуррентные соотношения и методы их решения Численное решение алгебраических и трансцендентных уравнений
Численное решение алгебраических и трансцендентных уравнений Десятичные дроби. Выполнить действия
Десятичные дроби. Выполнить действия Презентация на тему Буквенная запись свойств сложения и вычитания (5 класс)
Презентация на тему Буквенная запись свойств сложения и вычитания (5 класс)  Системы принятия решений
Системы принятия решений Корень степени n
Корень степени n Начальные геометрические сведения. Признаки равенства треугольников
Начальные геометрические сведения. Признаки равенства треугольников