Содержание
- 2. Основные понятия - мнимая единица (i - от французского imaginaire – «мнимый») а - называется действительной
- 3. Если a = 0, то ib – чисто мнимое число. Если b = 0, то получаем
- 4. Основные понятия
- 5. О M (a;b) x y b a ϕ Геометрическое изображение комплексного числа модуль комплексного числа аргумент
- 6. Алгебраическая, тригонометрическая форма записи комплексного числа ⇒
- 7. Алгебраическая, тригонометрическая и форма записи комплексного числа - алгебраическая форма; - тригонометрическая форма;
- 8. Действия с комплексными числами В алгебраической форме Суммой двух комплексных чисел называется комплексное число, определяемое равенством
- 9. Действия с комплексными числами Произведением комплексных чисел называется такое комплексное число, которое получается, если перемножить числа
- 10. Действия с комплексными числами Частным от деления z1 на z2 называется комплексное число z , удовлетворяющее
- 11. Действия с комплексными числами В тригонометрической форме При умножении комплексных чисел в тригономет-рической форме их модули
- 12. Действия с комплексными числами. Формула Муавра Для нахождения частного двух комплексных чисел в тригонометрической и показательной
- 14. Скачать презентацию











 Особенности математических моделей, влияющих на выбор методов
Особенности математических моделей, влияющих на выбор методов Алгебра логики
Алгебра логики Математический маятник. Измерения
Математический маятник. Измерения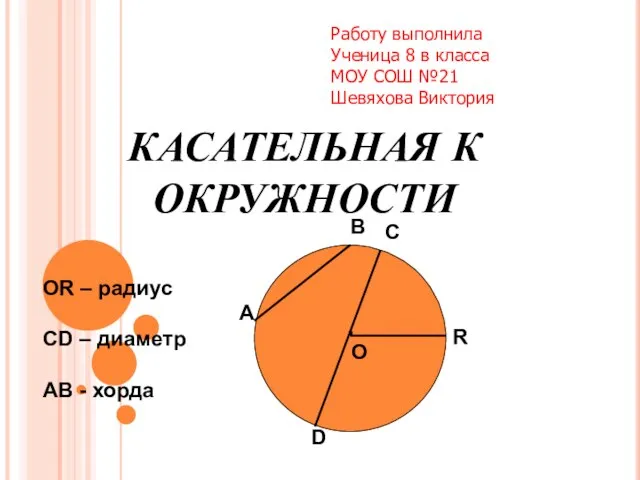 Презентация на тему Касательная к окружности
Презентация на тему Касательная к окружности  Треугольники (элементы, площади)
Треугольники (элементы, площади) Признаки подобия треугольников
Признаки подобия треугольников Старинные единицы измерения. Меры и массы и объемы
Старинные единицы измерения. Меры и массы и объемы На что похож наш ноль?
На что похож наш ноль? Презентация на тему СВОЙСТВА ДВИЖЕНИЯ
Презентация на тему СВОЙСТВА ДВИЖЕНИЯ  Презентация на тему Виды многогранников
Презентация на тему Виды многогранников  Уравнение окружности и прямой
Уравнение окружности и прямой Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов 2020.09.03 Десятичная система записи натуральных чисел
2020.09.03 Десятичная система записи натуральных чисел Предмет математика. Счёт предметов. Один, два, три…
Предмет математика. Счёт предметов. Один, два, три… Килограмм. Фрагмент урока
Килограмм. Фрагмент урока Метод Гаусса для решения систем линейных уравнений
Метод Гаусса для решения систем линейных уравнений Как помочь учащимся легче воспринимать новый материал
Как помочь учащимся легче воспринимать новый материал Перпендикулярные прямые. Самостоятельная работа
Перпендикулярные прямые. Самостоятельная работа Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Показательная функция. Порядок роста и убывания функции
Показательная функция. Порядок роста и убывания функции Шкала отношений
Шкала отношений Подготовка к ГИА по математике. Задания 10
Подготовка к ГИА по математике. Задания 10 Розв'язання задач
Розв'язання задач Предел функции
Предел функции Числовая окружность
Числовая окружность Численное интегрирование. Метод средних прямоугольников
Численное интегрирование. Метод средних прямоугольников Предел последовательности. Лекция 3
Предел последовательности. Лекция 3 Сфера и шар
Сфера и шар