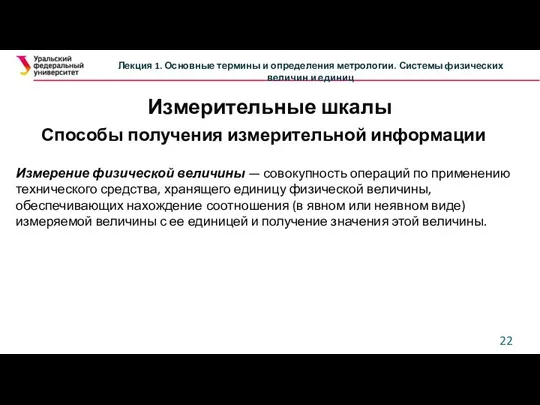
и ее истинное значение.
Следствие А1.
Для данной физической величины объекта измерения существует множество измеряемых величин (и соответственно их истинных значений).
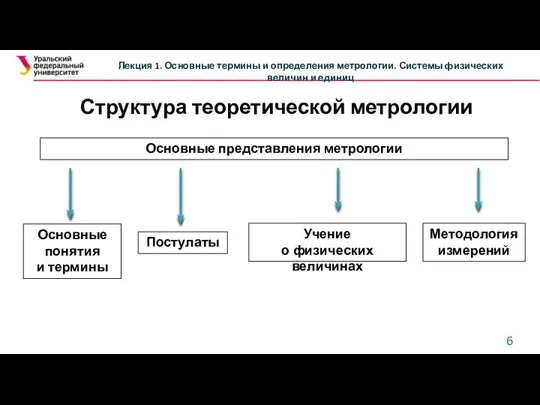
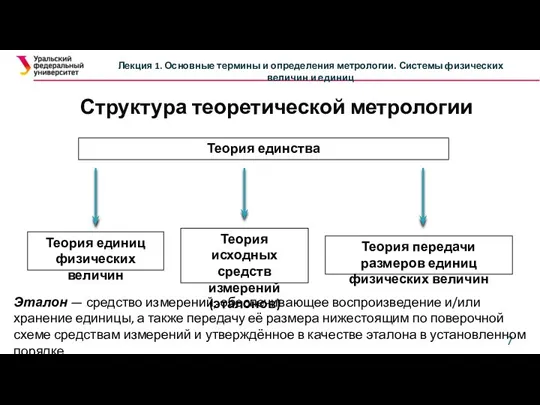
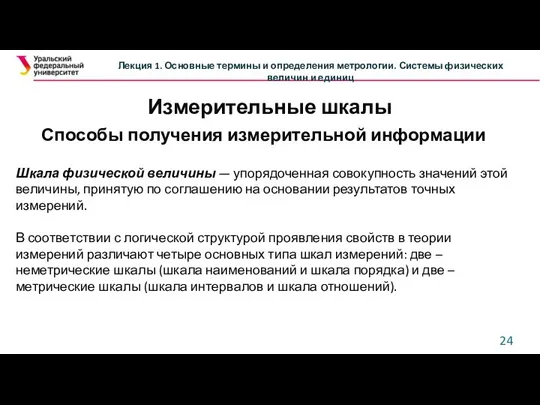
Как и любая другая наука, теория измерений (метрология) строится на основе ряда основополагающих постулатов, описывающих ее исходные аксиомы.
Первым постулатом теории измерений является постулат А: в рамках принятой модели объекта исследования существует определенная физическая величина и ее истинное значение.
Если считать, что деталь представляет собой цилиндр (модель – цилиндр), то она имеет диаметр, который может быть измерен. Если же деталь нельзя считать цилиндрической, например, ее сечение представляет собой эллипс, то измерять ее диаметр бессмысленно, поскольку измеренное значение не несет полезной информации о детали. И, следовательно, в рамках новой модели диаметр не существует. Измеряемая величина существует лишь в рамках принятой модели, то есть имеет смысл только до тех пор, пока модель признается адекватной объекту. Так как при различных целях исследований данному объекту могут быть сопоставлены различные модели, то из постулата А вытекает
следствие А1: для данной физической величины объекта измерения существует множество измеряемых величин (и соответственно их истинных значений).
Из первого постулата теории измерений следует, что измеряемому свойству объекта измерений должен соответствовать некоторый параметр его модели. Данная модель в течение времени, необходимого для измерения, должна позволять считать этот параметр неизменным. В противном случае измерения не могут быть проведены.
Указанный факт описывается постулатом В: истинное значение измеряемой величины постоянно.
Выделив постоянный параметр модели, можно перейти к измерению соответствующей величины. Для переменной физической величины необходимо выделить или выбрать некоторый постоянный параметр и измерить его. В общем случае такой постоянный параметр вводится с помощью некоторого функционала. Примером таких постоянных параметров переменных во времени сигналов, вводимых посредством функционалов, являются средневыпрямленные или среднеквадратические значения. Данный аспект отражается в
следствии В1: для измерения переменной физической величины необходимо определить ее постоянный параметр – измеряемую величину.
При построении математической модели объекта измерения неизбежно приходится идеализировать те или иные его свойства.
Модель никогда не может полностью описывать все свойства объекта измерений. Она отражает с определенной степенью приближения некоторые из них, имеющие существенное значение для решения данной измерительной задачи. Модель строится до измерения на основе априорной информации об объекте и с учетом цели измерения.
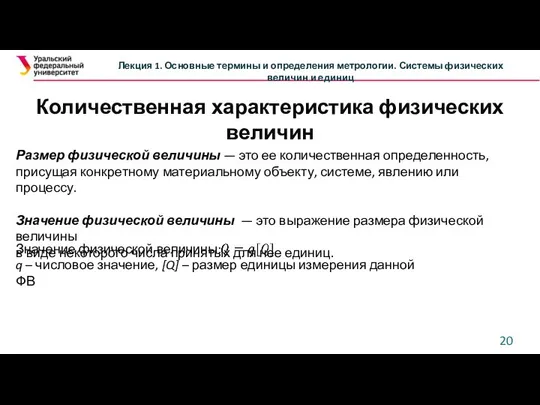
Измеряемая величина определяется как параметр принятой модели, а его значение, которое можно было бы получить в результате абсолютно точного измерения, принимается в качестве истинного значения данной измеряемой величины. Эта неизбежная идеализация, принятая при построении модели объекта измерения, обусловливает
неизбежное несоответствие между параметром модели и реальным свойством объекта, которое называется пороговым.
Принципиальный характер понятия «пороговое несоответствие» устанавливается постулатом С: существует несоответствие измеряемой величины исследуемому свойству объекта (пороговое несоответствие измеряемой величины).
Пороговое несоответствие принципиально ограничивает достижимую точность измерений при принятом определении измеряемой физической величины.
Изменения и уточнения цели измерения, в том числе и такие, которые требуют повышения точности измерений, приводят к необходимости изменять или уточнять модель объекта измерений и переопределять понятие измеряемой величины. Основной причиной переопределения является то, что пороговое несоответствие ранее принятого определения не позволяет повысить точность измерения до уровня требуемой. Вновь введенный измеряемый параметр модели также может быть измерен лишь с погрешностью, которая в лучшем
случае равна погрешности, обусловленной пороговым несоответствием. Поскольку принципиально невозможно построить абсолютно адекватную модель объекта измерения, то нельзя
устранить пороговое несоответствие между измеряемой физической величиной и описывающим ее параметром модели объекта измерений.
Отсюда вытекает важное следствие С1: истинное значение измеряемой величины отыскать невозможно.
Модель можно построить только при наличии априорной информации об объекте измерения. При этом, чем больше информации, тем более адекватной будет модель и соответственно точнее и правильнее будет выбран ее параметр, описывающий измеряемую физическую величину. Следовательно, увеличение априорной информации уменьшает пороговое несоответствие.
Данная ситуация отражается в следствииС2: достижимая точность измерения определяется априорной информацией об объекте измерения.
Из этого следствия вытекает, что при отсутствии априорной информации измерение принципиально невозможно. В то же время максимально возможная априорная информация заключается в известной оценке измеряемой величины, точность которой равна требуемой. В этом случае необходимости в измерении нет.
Лекция 1. Основные термины и определения метрологии. Системы физических величин и единиц






















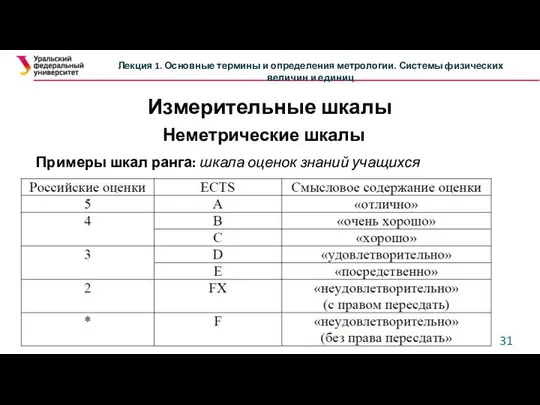






















 Презентация на тему Тренажёр «Квадратные корни»
Презентация на тему Тренажёр «Квадратные корни»  Математический тренажёр
Математический тренажёр Презентация на тему ПОНЯТИЕ ЛОГАРИФМА
Презентация на тему ПОНЯТИЕ ЛОГАРИФМА  Приёмы вычитания с переходом через 10
Приёмы вычитания с переходом через 10 Матричный способ решения СЛАУ и метод Крамера
Матричный способ решения СЛАУ и метод Крамера Взвешенные графы. Остовные деревья. Кратчайшие пути
Взвешенные графы. Остовные деревья. Кратчайшие пути Веселая математика. Головоломки
Веселая математика. Головоломки Гипотеза Коллатца. (доказательство гипотезы)
Гипотеза Коллатца. (доказательство гипотезы) Сокращение дробей. Самоанализ
Сокращение дробей. Самоанализ Сечение геометрических тел плоскостями
Сечение геометрических тел плоскостями Старинные меры длины
Старинные меры длины Общие методы решения уравнений
Общие методы решения уравнений Метод координат
Метод координат Площадь. Фигуры
Площадь. Фигуры Понятия и свойства функции. Предел функции
Понятия и свойства функции. Предел функции Округление десятичных дробей
Округление десятичных дробей Многогранники. Тела Архимеда
Многогранники. Тела Архимеда Арифметические операции в разных системах счисления
Арифметические операции в разных системах счисления Комбинаторика. Факториал. Вычисление факториала. Формула числа перестановок, размещений и сочетаний
Комбинаторика. Факториал. Вычисление факториала. Формула числа перестановок, размещений и сочетаний Зашифрованное слово
Зашифрованное слово Расчет параметров слоев
Расчет параметров слоев Презентация на тему Уменьшаемое. Вычитаемое. Значение разности
Презентация на тему Уменьшаемое. Вычитаемое. Значение разности  Презентация по математике "Отношение больше, меньше" -
Презентация по математике "Отношение больше, меньше" -  Решение уравнений методом замены переменной
Решение уравнений методом замены переменной Простейшие преобразования графиков
Простейшие преобразования графиков Создание математической модели
Создание математической модели Согласование подходов к проверке заданий с развернутым ответом. Задания 22, 25
Согласование подходов к проверке заданий с развернутым ответом. Задания 22, 25 Тренажер таблицы умножения
Тренажер таблицы умножения