Содержание
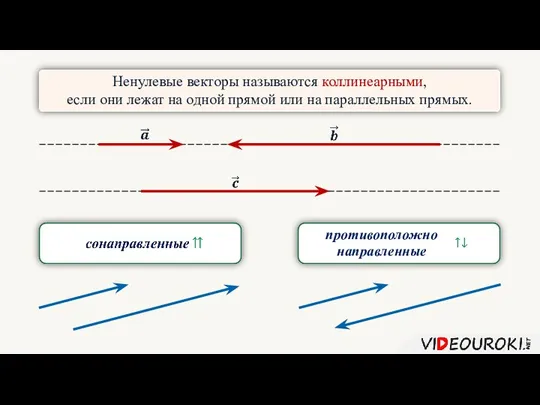
- 3. Ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. противоположно направленные
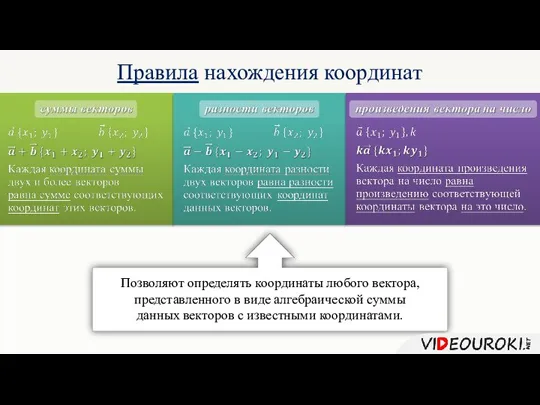
- 5. Сумма векторов Правило многоугольника Правило треугольника Правило параллелограмма
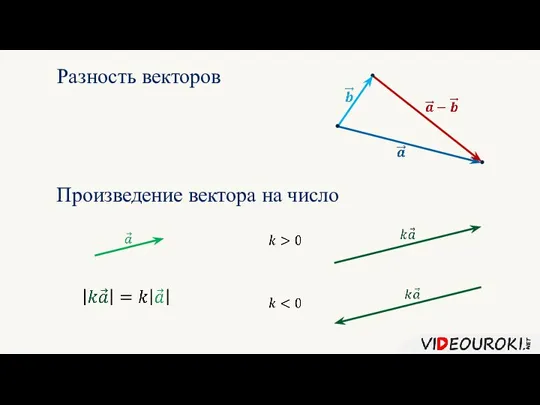
- 6. Разность векторов Произведение вектора на число
- 7. Теорема. На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются
- 9. Правила нахождения координат Позволяют определять координаты любого вектора, представленного в виде алгебраической суммы данных векторов с
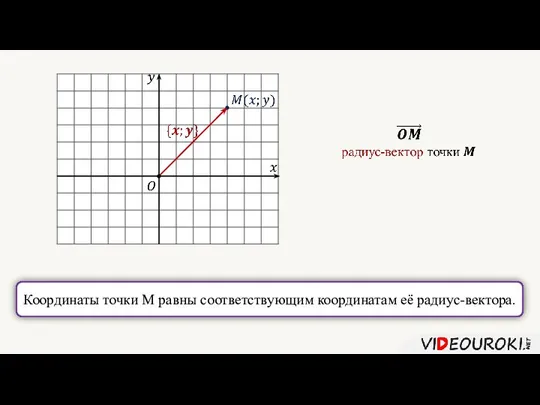
- 10. Координаты точки М равны соответствующим координатам её радиус-вектора.
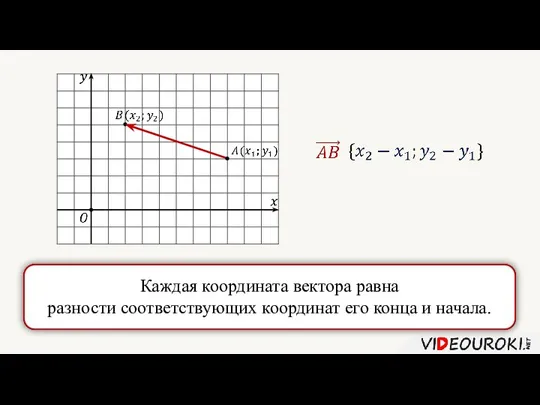
- 11. Каждая координата вектора равна разности соответствующих координат его конца и начала.
- 12. понятие вектора действия над векторами координаты вектора
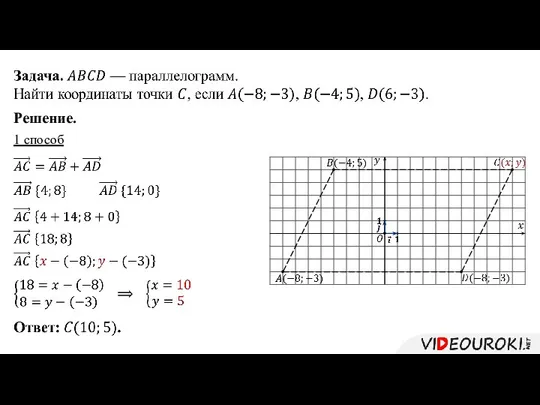
- 13. Решение. 1 способ
- 14. понятие вектора действия над векторами координаты вектора метод координат
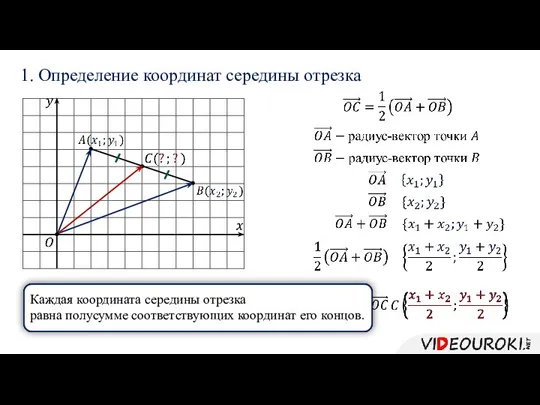
- 15. 1. Определение координат середины отрезка Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
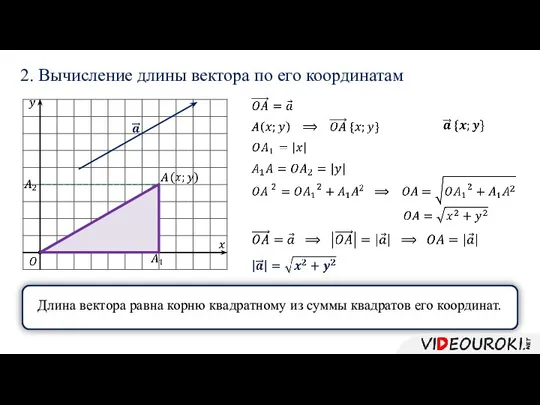
- 18. 2. Вычисление длины вектора по его координатам Длина вектора равна корню квадратному из суммы квадратов его
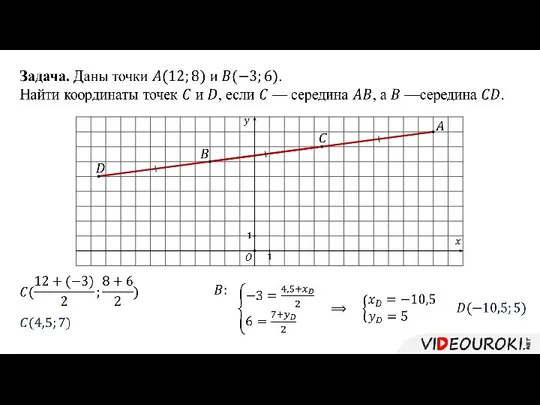
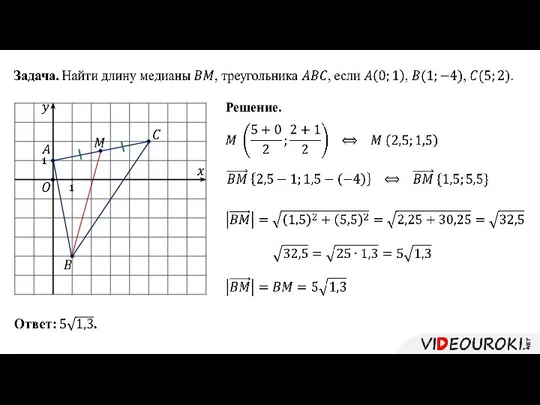
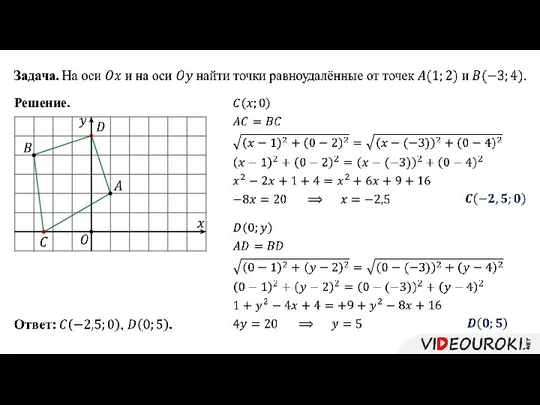
- 20. Решение.
- 21. 3. Определение расстояния между двумя точками
- 22. Решение.
- 24. Скачать презентацию







 Скалярное прозведение векторов
Скалярное прозведение векторов Решение задач
Решение задач Преобразования графиков функций. 8 класс
Преобразования графиков функций. 8 класс Признаки параллельности прямых. Тест
Признаки параллельности прямых. Тест Лекция_04
Лекция_04 Среднее арифметическое
Среднее арифметическое Квадратичная зависимость
Квадратичная зависимость Логарифмы вокруг нас
Логарифмы вокруг нас Диофантово уравнение
Диофантово уравнение Проценты
Проценты Задачи на построение сечений
Задачи на построение сечений Элективный курс. Алгебра 11 класс. Уроки 07-08
Элективный курс. Алгебра 11 класс. Уроки 07-08 Интегралы. Введение в математический анализ
Интегралы. Введение в математический анализ Связь между суммой и слагаемыми (1 класс)
Связь между суммой и слагаемыми (1 класс) Волшебная страна математики: основы математики для детей 5-6 лет
Волшебная страна математики: основы математики для детей 5-6 лет Названия чисел в записях действий
Названия чисел в записях действий Основные формулы
Основные формулы Задачи на совместную работу
Задачи на совместную работу Проверка деления
Проверка деления Презентация на тему Треугольники. Третий признак равенства
Презентация на тему Треугольники. Третий признак равенства  Математическая статистика 2
Математическая статистика 2 Факториал. Задача со стульями
Факториал. Задача со стульями Геометричне моделювання організаційних кластерних сруктур
Геометричне моделювання організаційних кластерних сруктур Логарифмы. Возведение в степень. Логарифмирование
Логарифмы. Возведение в степень. Логарифмирование Окружность и круг
Окружность и круг Презентация на тему Решение систем линейных уравнений 7 класс для учителя
Презентация на тему Решение систем линейных уравнений 7 класс для учителя  Метод Крамера
Метод Крамера Презентация на тему Зарождение и история геометрии
Презентация на тему Зарождение и история геометрии