Признаки равенства треугольников

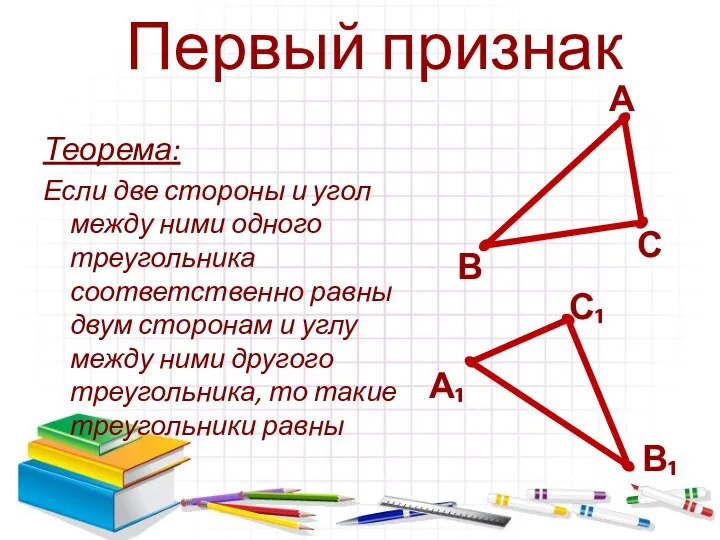
Теорема:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Первый признак

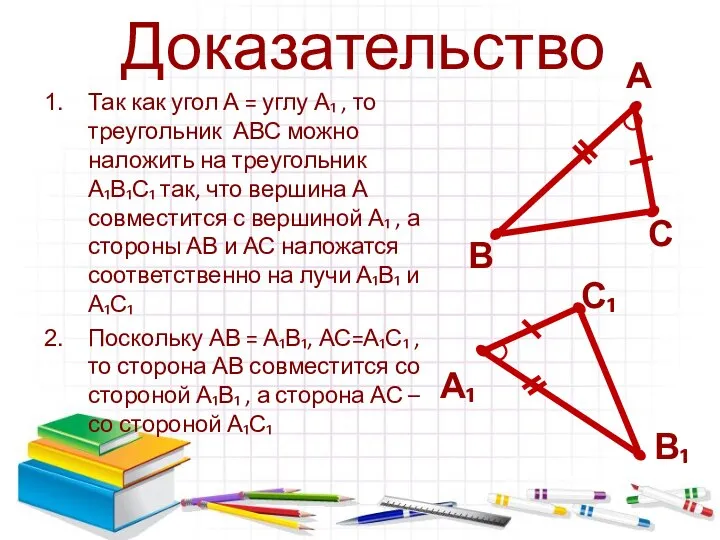
Доказательство
Так как угол А = углу А₁ , то треугольник АВС можно наложить на треугольник А₁В₁С₁ так, что вершина А совместится с вершиной А₁ , а стороны АВ и АС наложатся соответственно на лучи А₁В₁ и А₁С₁
Поскольку АВ = А₁В₁, АС=А₁С₁ , то сторона АВ совместится со стороной А₁В₁ , а сторона АС – со стороной А₁С₁
А
В
С
А₁
В₁
С₁

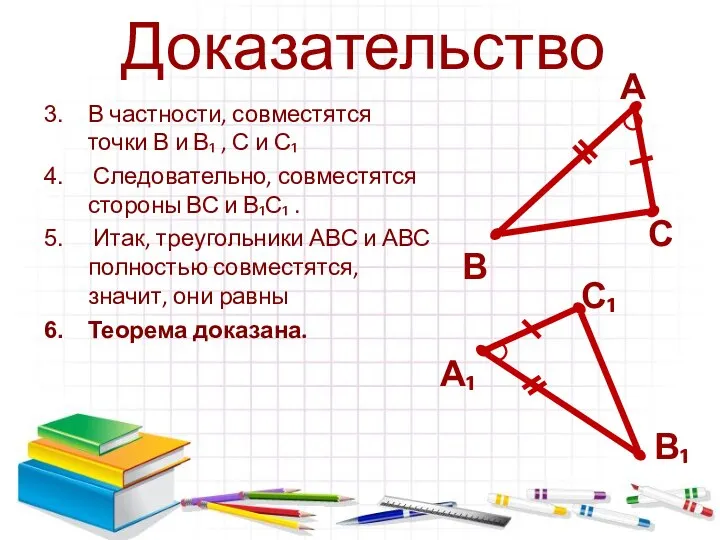
Доказательство
В частности, совместятся точки В и В₁ , С и С₁ Следовательно, совместятся стороны ВС и В₁С₁ .
Итак, треугольники АВС и АВС полностью совместятся, значит, они равны
Теорема доказана.
А
В
С
А₁
В₁
С₁

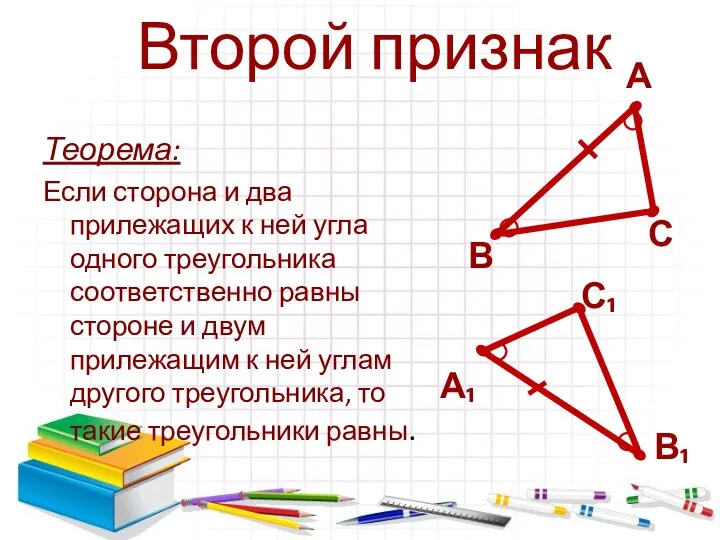
Теорема:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Второй признак
С
В₁

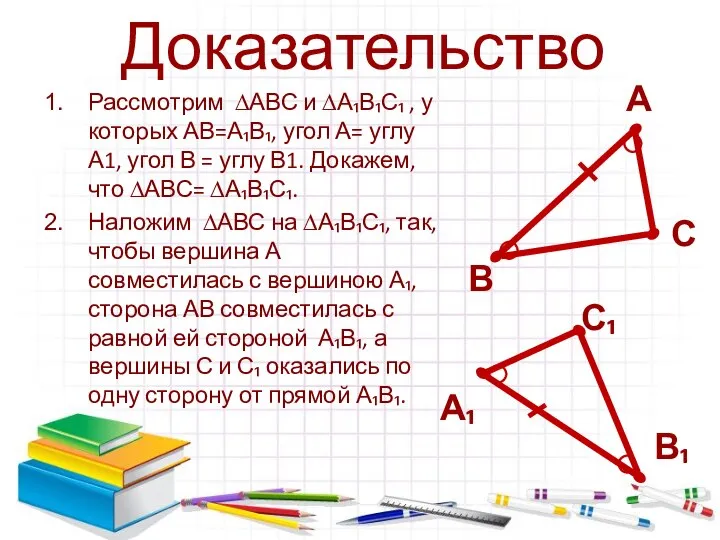
Доказательство
Рассмотрим ∆АВС и ∆А₁В₁С₁ , у которых АВ=А₁В₁, угол А= углу А1, угол В = углу В1. Докажем, что ∆АВС= ∆А₁В₁С₁.
Наложим ∆АВС на ∆А₁В₁С₁, так, чтобы вершина А совместилась с вершиною А₁, сторона АВ совместилась с равной ей стороной А₁В₁, а вершины С и С₁ оказались по одну сторону от прямой А₁В₁.
А
В
А₁
С₁
В₁
С

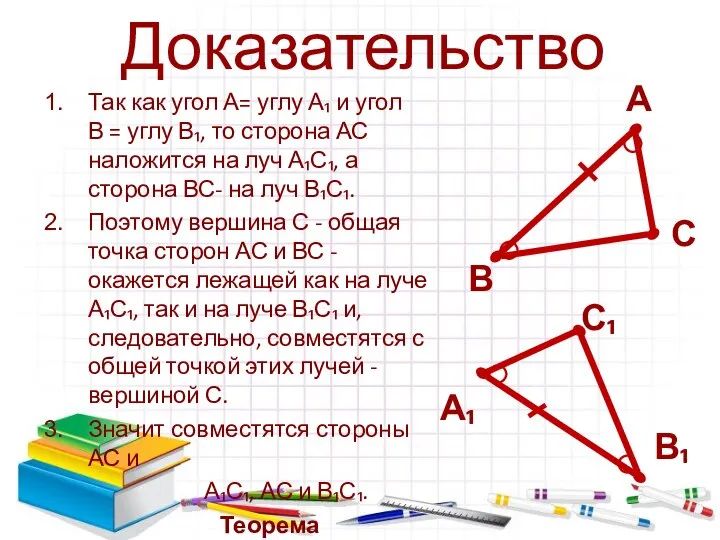
Доказательство
Так как угол А= углу А₁ и угол В = углу В₁, то сторона АС наложится на луч А₁С₁, а сторона ВС- на луч В₁С₁.
Поэтому вершина С - общая точка сторон АС и ВС - окажется лежащей как на луче А₁С₁, так и на луче В₁С₁ и, следовательно, совместятся с общей точкой этих лучей - вершиной С.
Значит совместятся стороны АС и
А₁С₁, АС и В₁С₁.
Теорема доказана.
А
В
А₁
С₁
В₁
С

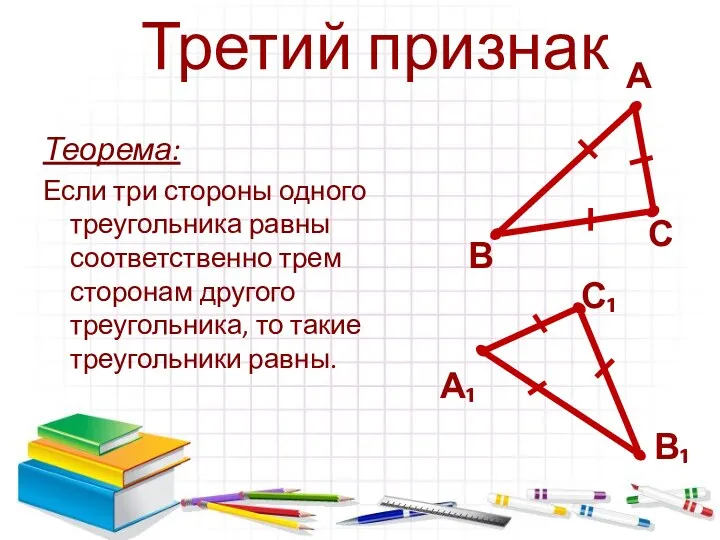
Теорема:
Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Третий признак

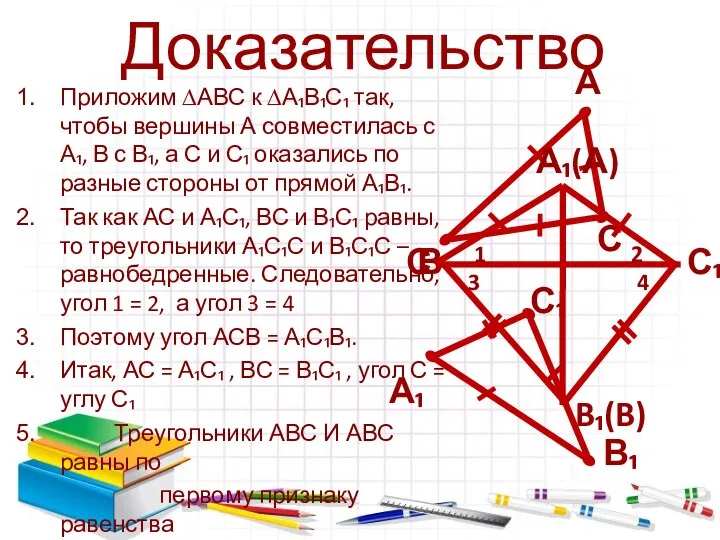
Доказательство
Приложим ∆АВС к ∆А₁В₁С₁ так, чтобы вершины А совместилась с А₁, В с В₁, а С и С₁ оказались по разные стороны от прямой А₁В₁.
Так как АС и А₁С₁, ВС и В₁С₁ равны, то треугольники А₁С₁С и В₁С₁С – равнобедренные. Следовательно, угол 1 = 2, а угол 3 = 4
Поэтому угол АСВ = А₁С₁В₁.
Итак, АС = А₁С₁ , ВС = В₁С₁ , угол С = углу С₁
Треугольники АВС И АВС равны по
первому признаку равенства Теорема доказана

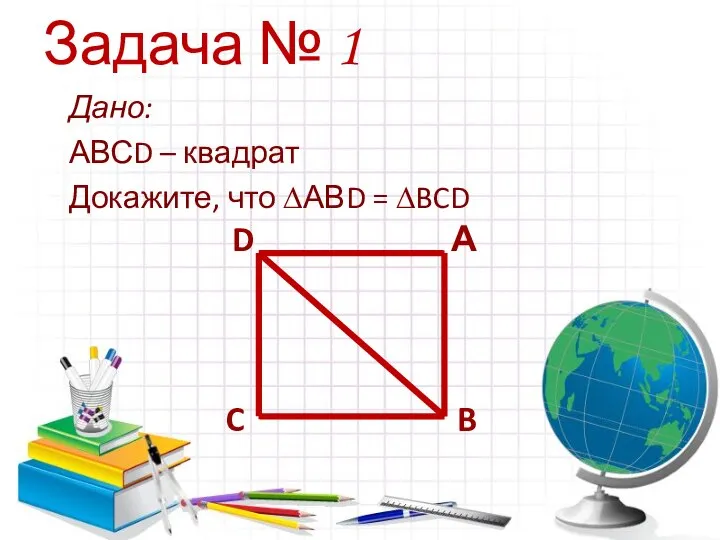
Задача № 1
Дано:
АВСD – квадрат
Докажите, что ∆АВD = ∆BCD

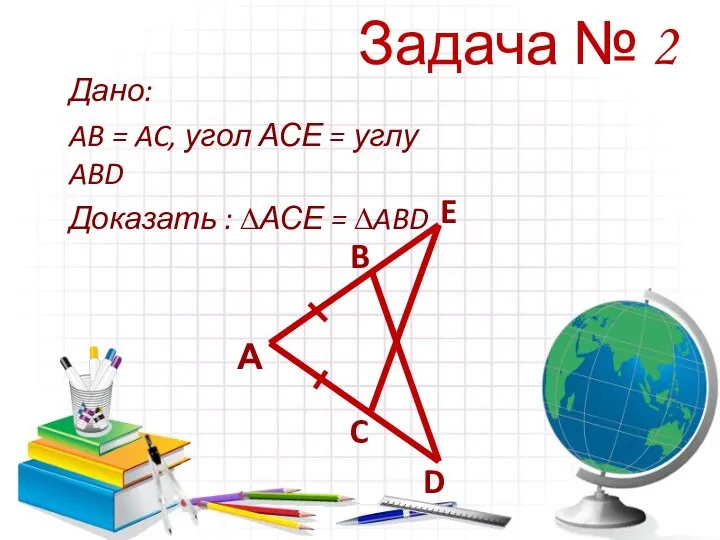
Задача № 2
Дано:
AB = AC, угол АСЕ = углу ABD
Доказать : ∆АСЕ = ∆ABD

Задача № 3
Дано:
Отрезки BЕ и AC точкой D делятся пополам.
Доказать : угол AED= углу CBD