Содержание
- 2. Термин “пирамида” заимствован из греческого “пирамис” или “пирамидос”. Греки в свою очередь позаимствовали это слово, как
- 3. На окраине Каира - столицы современного Египта самая высокая - пирамида Хеопса
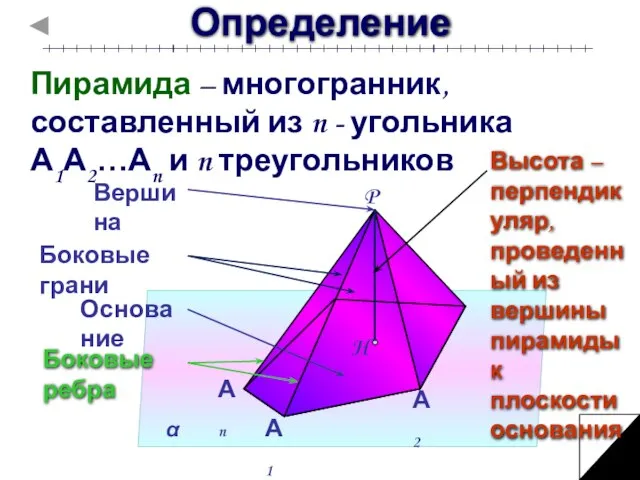
- 4. Определение Пирамида – многогранник, составленный из n - угольника А1А2…Аn и n треугольников Высота – перпендикуляр,
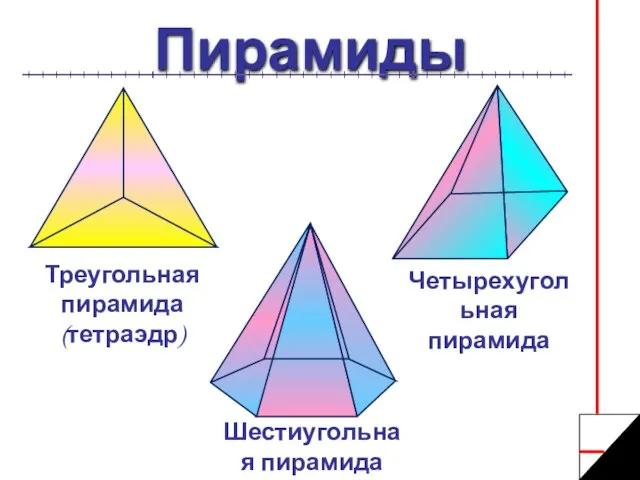
- 5. Пирамиды Треугольная пирамида (тетраэдр) Шестиугольная пирамида Четырехугольная пирамида
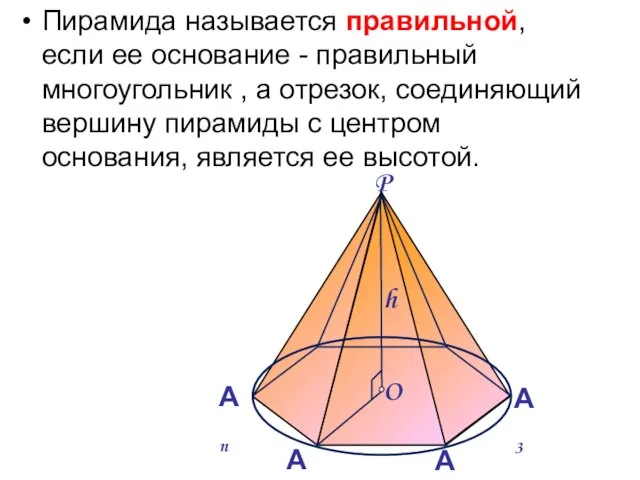
- 6. Пирамида называется правильной, если ее основание - правильный многоугольник , а отрезок, соединяющий вершину пирамиды с
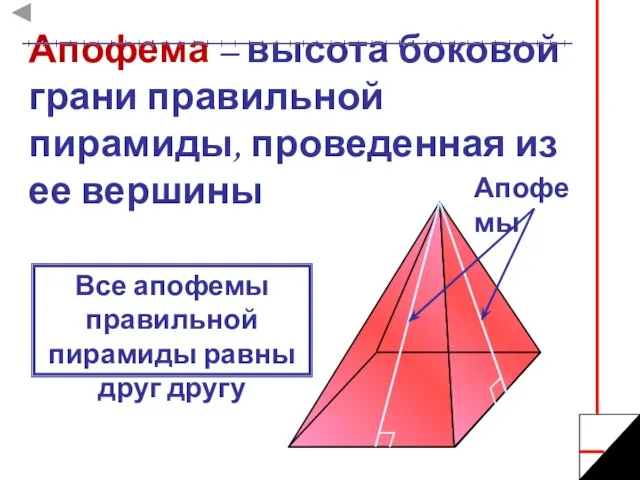
- 7. Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины Апофемы Все апофемы правильной пирамиды
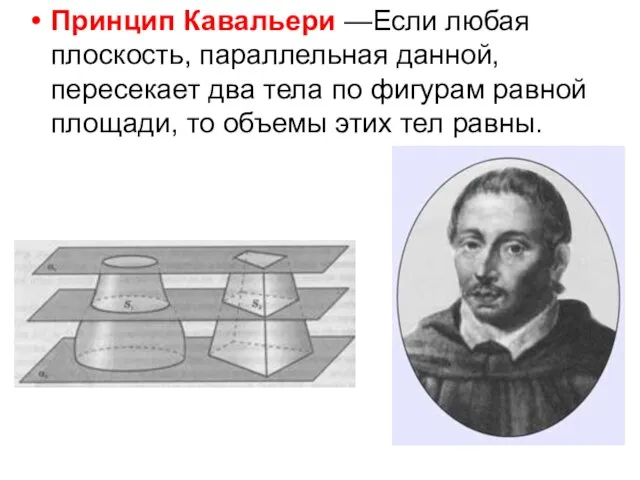
- 8. Принцип Кавальери —Если любая плоскость, параллельная данной, пересекает два тела по фигурам равной площади, то объемы
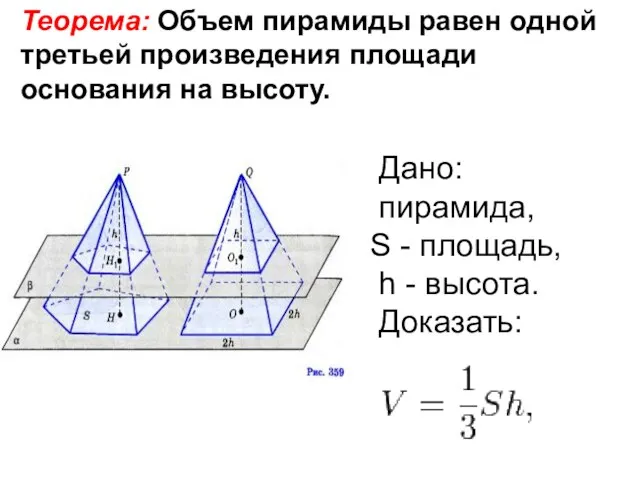
- 9. Теорема: Объем пирамиды равен одной третьей произведения площади основания на высоту. Дано: пирамида, S - площадь,
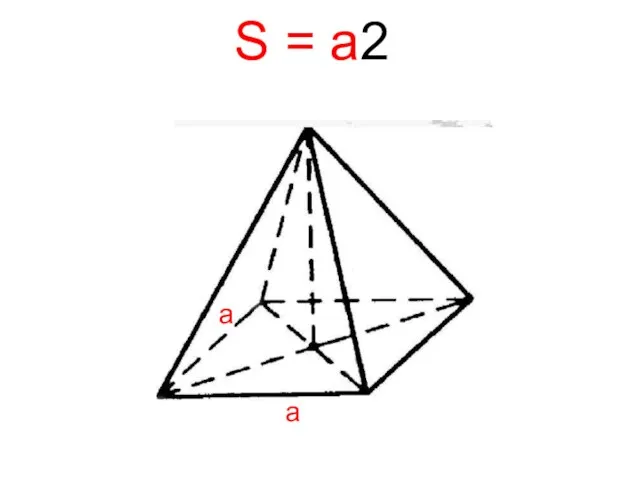
- 10. S = a2 а а
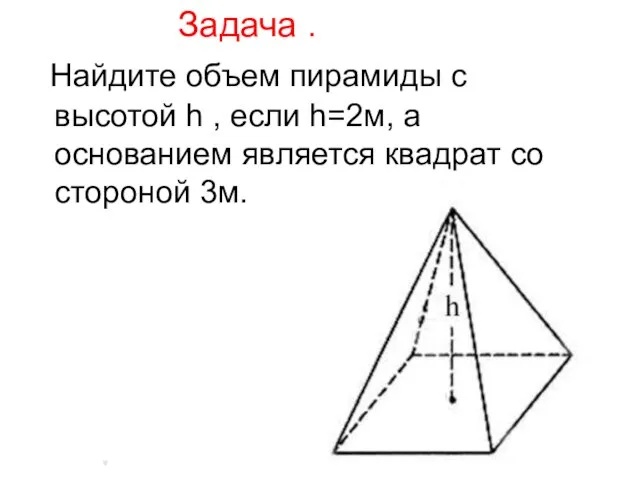
- 11. Задача . Найдите объем пирамиды с высотой h , если h=2м, а основанием является квадрат со
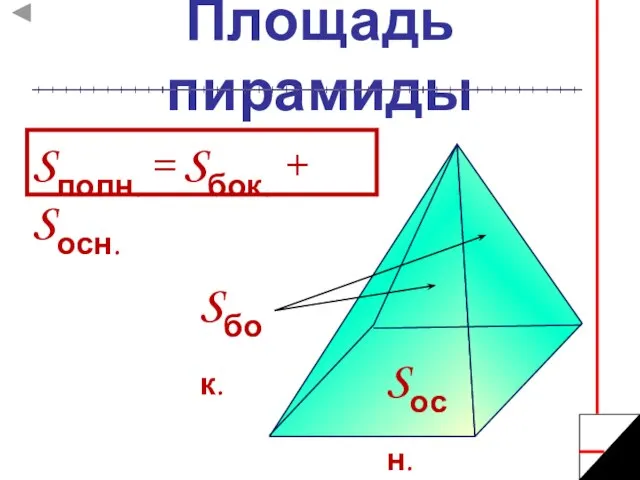
- 12. Площадь пирамиды Sполн. = Sбок. + Sосн. Sбок. Sосн.
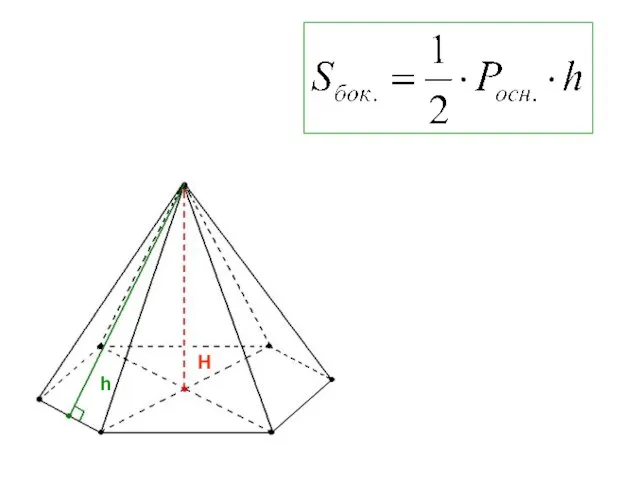
- 13. h H
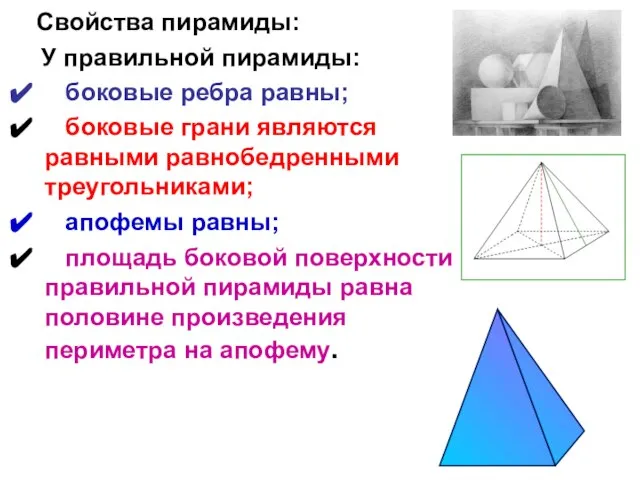
- 14. Свойства пирамиды: У правильной пирамиды: боковые ребра равны; боковые грани являются равными равнобедренными треугольниками; апофемы равны;
- 17. Скачать презентацию



 Комплексные числа и координатная плоскость. Решение примеров на построение комплексных чисел на комплексной плоскости
Комплексные числа и координатная плоскость. Решение примеров на построение комплексных чисел на комплексной плоскости Решение показателей уравнений
Решение показателей уравнений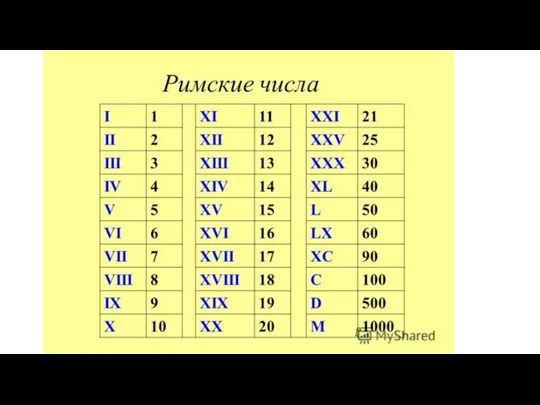 Римские числа
Римские числа Повторительно-обобщающий урок по теме: Показательная функция. 11 класс
Повторительно-обобщающий урок по теме: Показательная функция. 11 класс Теоремы о пределах. Нахождение пределов
Теоремы о пределах. Нахождение пределов Презентация на тему Средняя линия треугольника
Презентация на тему Средняя линия треугольника  Реши примеры устно. 2 класс
Реши примеры устно. 2 класс Декартова система координат
Декартова система координат Презентация на тему Математический КВН
Презентация на тему Математический КВН  Отображения (функции)
Отображения (функции) Диалектика как методология научного познания
Диалектика как методология научного познания Экологические понятия в математике
Экологические понятия в математике Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА Параллельные прямые. 7 класс
Параллельные прямые. 7 класс Научные открытия России. Задача тысячелетия. Теорема Пуанкаре
Научные открытия России. Задача тысячелетия. Теорема Пуанкаре Дифференциальные уравнения и их применение в медицине
Дифференциальные уравнения и их применение в медицине Динамика системы вблизи цикла
Динамика системы вблизи цикла Деление с остатком
Деление с остатком Парная линейная регрессия
Парная линейная регрессия Компоненти дій
Компоненти дій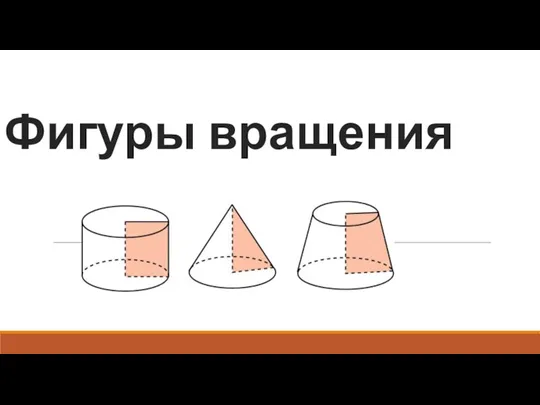 Фигуры вращения
Фигуры вращения Элементы комбинаторики. Решение простейших комбинаторных задач
Элементы комбинаторики. Решение простейших комбинаторных задач Таблица умножения с 7 до 9
Таблица умножения с 7 до 9 Производная и первообразная
Производная и первообразная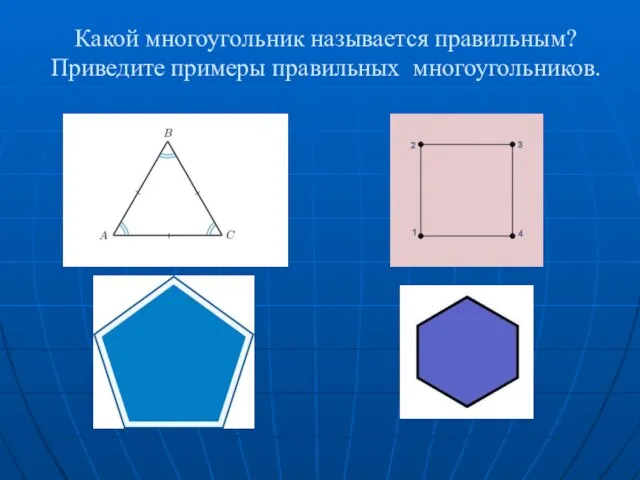 Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Занимательные задачи
Занимательные задачи Основное свойство дроби
Основное свойство дроби