Кроссворд по теме Треугольники. 7 класс

Один мудрец сказал:
«Высшее проявление духа — это разум.
Высшее проявление разума — это геометрия. Клетка геометрии — треугольник. Он так же неисчерпаем, как и Вселенная. Окружность — душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но и возвысите душу свою».

Дорогие ребята!
Сегодня я хочу проверить, как вы знаете термины и понятия по теме «Треугольники».
Давайте заполним с вами кроссворд по изученному материалу. Разгадывается он следующим образом:
внимательно прочитайте вопрос, наберите на клавиатуре правильный ответ, перейдите (с помощью кнопки «дальше») на следующий слайд.

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Р
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
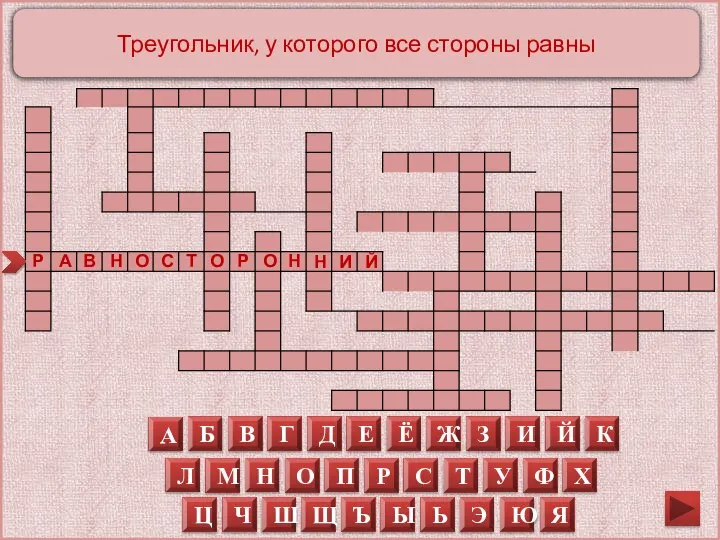
Треугольник, у которого все стороны равны

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
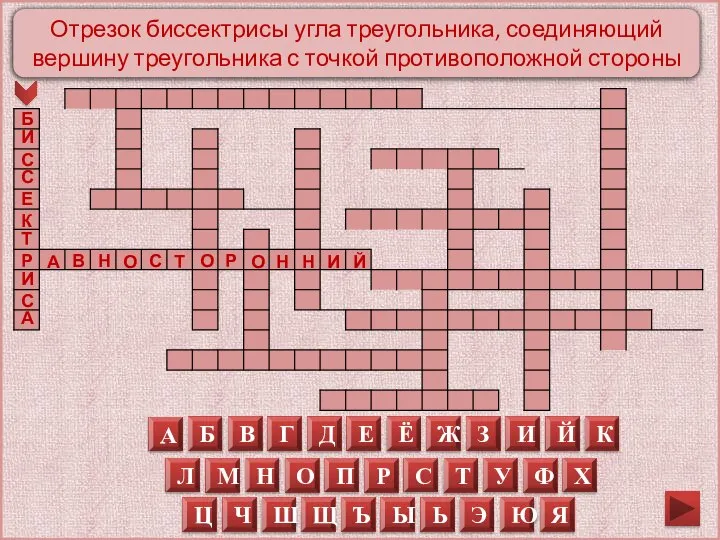
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
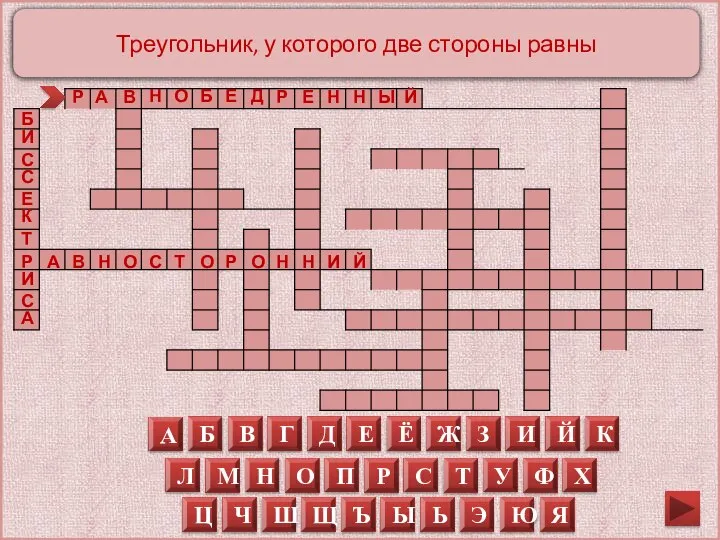
Треугольник, у которого две стороны равны

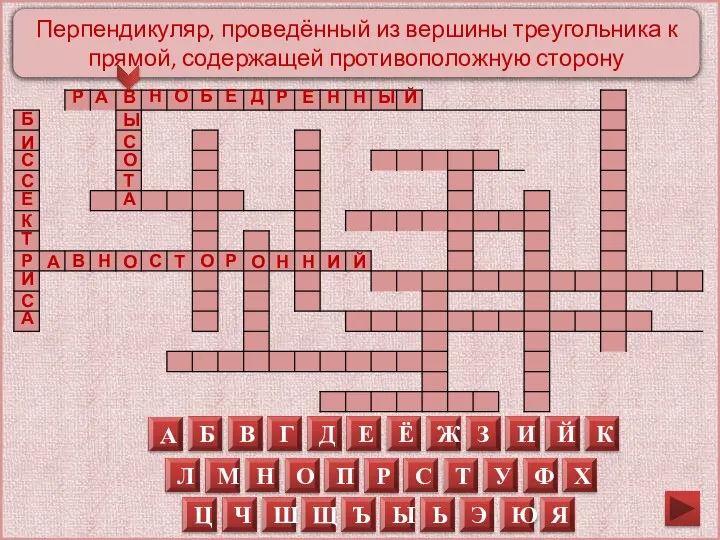
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону
А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
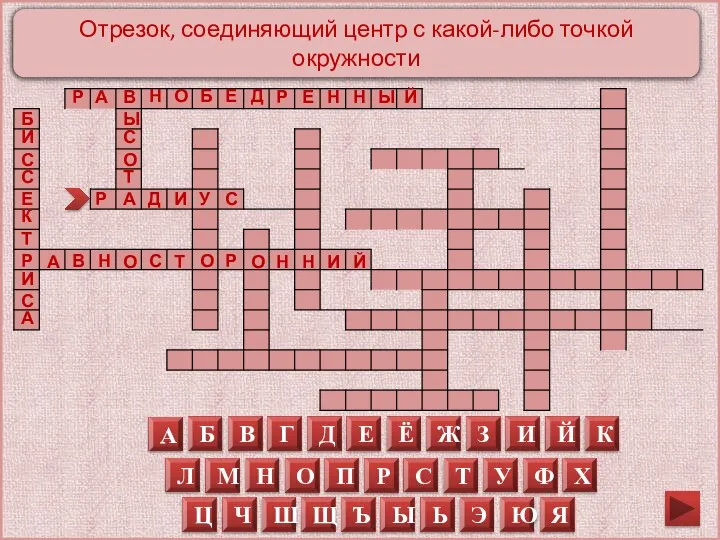
Отрезок, соединяющий центр с какой-либо точкой окружности

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
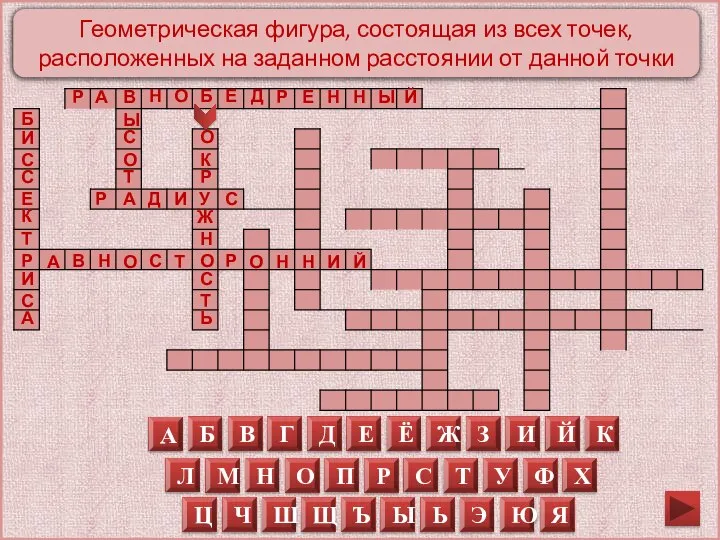
Геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
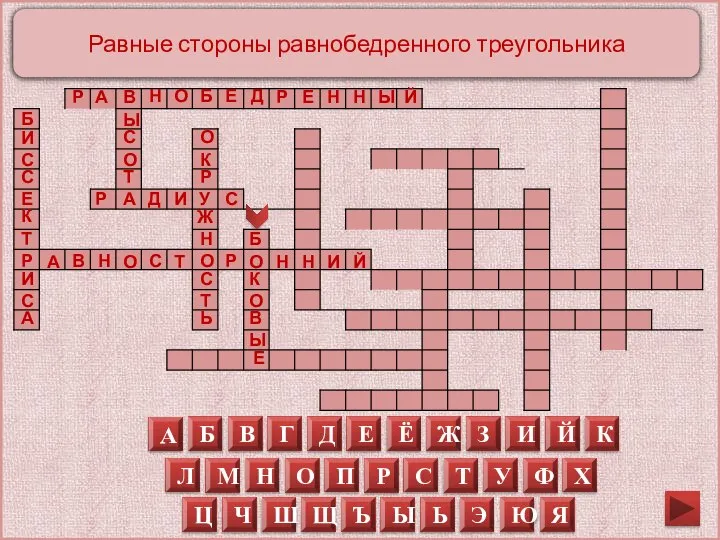
Равные стороны равнобедренного треугольника

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Равные стороны равнобедренного треугольника называются боковыми, а третья сторона – это ...

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Р
П
О
Д
Е
Л
Е
Н
И
Е
Предложение, в котором разъясняется смысл того или иного выражения

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Р
П
О
Д
Е
Л
Е
Н
И
Е
М
Е
Д
И
А
Н
А
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Р
П
О
Д
Е
Л
Е
Н
И
Е
М
Е
Д
И
А
Н
А
Т
У
П
У
Г
О
Л
Ь
Н
Ы
О
Й
Треугольник, у которого один угол тупой

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Р
П
О
Д
Е
Л
Е
Н
И
Е
М
Е
Д
И
А
Н
А
Т
У
П
У
Г
О
Л
Ь
Н
Ы
О
Й
О
С
Т
О
У
Г
О
Л
Ь
Н
Р
Ы
Й
Треугольник, у которого все углы острые

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Р
П
О
Д
Е
Л
Е
Н
И
Е
М
Е
Д
И
А
Н
А
Т
У
П
У
Г
О
Л
Ь
Н
Ы
О
Й
О
С
Т
О
У
Г
О
Л
Ь
Н
Р
Ы
Й
П
Е
Р
М
Е
Т
Р
И
Сумма длин трёх сторон треугольника

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Р
П
О
Д
Е
Л
Е
Н
И
Е
М
Е
Д
И
А
Н
А
Т
У
П
У
Г
О
Л
Ь
Н
Ы
О
Й
О
С
Т
О
У
Г
О
Л
Ь
Н
Р
Ы
Й
П
Е
Р
М
Е
Т
Р
И
Х
О
Р
А
Д
Отрезок, соединяющий две точки окружности

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Р
П
О
Д
Е
Л
Е
Н
И
Е
М
Е
Д
И
А
Н
А
Т
У
П
У
Г
О
Л
Ь
Н
Ы
О
Й
О
С
Т
О
У
Г
О
Л
Ь
Н
Р
Ы
Й
П
Е
Р
М
Е
Т
Р
И
Х
О
Р
А
Д
Е
Р
М
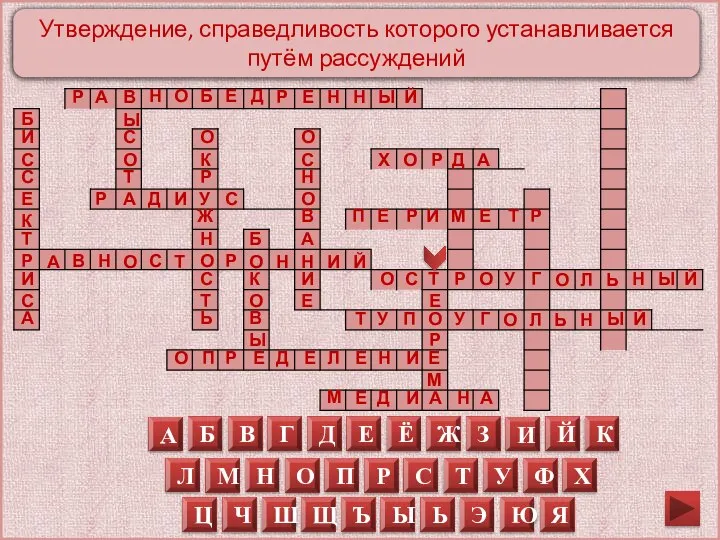
Утверждение, справедливость которого устанавливается путём рассуждений

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Р
П
О
Д
Е
Л
Е
Н
И
Е
М
Е
Д
И
А
Н
А
Т
У
П
У
Г
О
Л
Ь
Н
Ы
О
Й
О
С
Т
О
У
Г
О
Л
Ь
Н
Р
Ы
Й
П
Е
Р
М
Е
Т
Р
И
Х
О
Р
А
Д
Е
Р
М
И
А
Е
Т
Хорда, проходящая через центр окружности

А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Р
П
О
Д
Е
Л
Е
Н
И
Е
М
Е
Д
И
А
Н
А
Т
У
П
У
Г
О
Л
Ь
Н
Ы
О
Й
О
С
Т
О
У
Г
О
Л
Ь
Н
Р
Ы
Й
П
Е
Р
М
Е
Т
Р
И
Х
О
Р
А
Д
Е
Р
М
И
А
Е
Т
Т
У
И
Н
К
О
Е
Ь
Геометрическая фигура, составленная из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки

Треугольник, у которого один угол прямой
А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
Б
И
С
Е
К
Р
С
А
В
Н
О
С
Т
О
Р
О
Н
Н
И
Й
И
А
Т
С
Р
А
В
Н
О
Б
Е
Д
Р
Е
Н
Н
Ы
Й
Ы
С
О
Т
А
Р
Д
И
У
С
Р
К
О
Ж
Н
С
Т
Ь
Б
К
О
В
Ы
Е
А
И
Е
О
С
Н
О
В
Р
П
О
Д
Е
Л
Е
Н
И
Е
М
Е
Д
И
А
Н
А
Т
У
П
У
Г
О
Л
Ь
Н
Ы
О
Й
О
С
Т
О
У
Г
О
Л
Ь
Н
Р
Ы
Й
П
Е
Р
М
Е
Т
Р
И
Х
О
Р
А
Д
Е
Р
М
И
А
Е
Т
Т
У
И
Н
К
О
Е
Ь
П
Р
М
О
У
О
Л
Н
Г
Я
Й