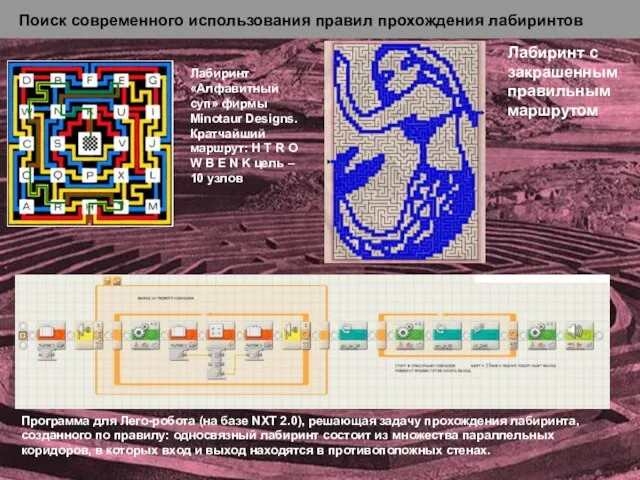
одно простое правило для прохождения лабиринта – правило "одной руки": двигаясь по лабиринту, надо все время касаться правой – красная линия (левой – синяя линия) рукой его стены. Этот алгоритм, вероятно, был известен еще древним грекам. Решая задачу прохождения лабиринта этим способом, я прошёл более длинный путь, касаясь стены правой рукой, и более короткий, касаясь стены левой рукой, но в итоге цель была достигнута.
Но для всех ли типов лабиринтов это правило применимо? Зачем разработан второй метод, если есть такое простое правило. Оказывается, правило руки применимо только к так называемым односвязным лабиринтам.
Односвязный лабиринт – это лабиринт, не содержащий замкнутых маршрутов, т.е. таких, которые образуют замкнутую петлю.
Замкнутый маршрут возникает в том случае, если существует ограниченный стенками «остров», который не соединяется с другими стенками лабиринта.
Лабиринт с одним или более островами называется многосвязным.
Первый многосвязный садовый лабиринт был сооружён в 1820-е годы в Чевнинге
в Великобритании.
В многосвязном лабиринте цели не достигнем, по правилу правой руки
Лабиринт [10]













 Графики функций
Графики функций Подготовка к ВПР
Подготовка к ВПР Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Aproximarea numerică a funcţiilor. Metode numerice – curs 11
Aproximarea numerică a funcţiilor. Metode numerice – curs 11 Признаки равенства треугольников
Признаки равенства треугольников Первообразная F'(x) = f(x)
Первообразная F'(x) = f(x) L_3_U
L_3_U Игра-тренажер Изучаем время
Игра-тренажер Изучаем время Презентация на тему Описательная статистика
Презентация на тему Описательная статистика  Презентация на тему Занимательная математика для детей (устный счёт + учимся писать цифры)
Презентация на тему Занимательная математика для детей (устный счёт + учимся писать цифры)  Сложение и вычитание чисел с разными знаками
Сложение и вычитание чисел с разными знаками Решение задач Параллельные прямые
Решение задач Параллельные прямые Задачи на построение
Задачи на построение Разложение на простые множители
Разложение на простые множители Исторические сведения
Исторические сведения Презентация на тему Сложение и вычитание именованных единиц
Презентация на тему Сложение и вычитание именованных единиц  Эталон и его назначение
Эталон и его назначение Решение логических задач
Решение логических задач Решение задач ( 8 класс)
Решение задач ( 8 класс) Тригонометрия. ЕГЭ, задание 7
Тригонометрия. ЕГЭ, задание 7 Семинар по математике
Семинар по математике Прямоугольник. Признак прямоугольника
Прямоугольник. Признак прямоугольника Измерение и построение углов
Измерение и построение углов График функции y = а(х – х0) +у0
График функции y = а(х – х0) +у0 Бинарный урок физики и геометрии
Бинарный урок физики и геометрии Презентация на тему Таблицы умножения и деления с числом 6
Презентация на тему Таблицы умножения и деления с числом 6  Проценты в медицине
Проценты в медицине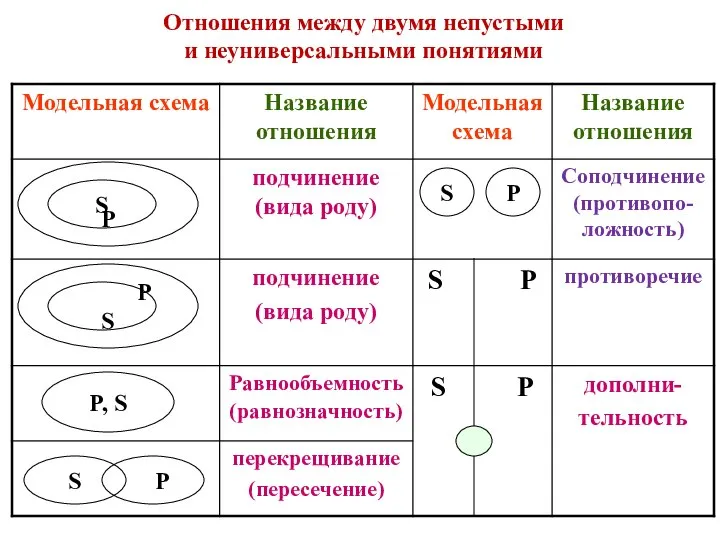 Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема
Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема