Содержание
- 2. Теория вероятностей и математическая статистика. Введение Цель лекции: познакомить с предметом теории вероятностей и математической статистики,
- 3. Теория вероятностей и математическая статистика. Введение Содержание лекции: - исторические сведения -предмет теории вероятностей -пространство элементарных
- 4. Теория вероятностей и математическая статистика. Введение Предмет теории вероятностей
- 5. Теория вероятностей и математическая статистика. Введение Блез Паскаль, 19 июня 1623, Клермон-Ферран, Франция — 19 августа
- 6. Теория вероятностей и математическая статистика. Введение Пьер де Ферма́ (17 августа 1601 — 12 января 1665,
- 7. Христиа́н Гю́йгенс ван Зёйлихем, (14 апреля 1629, — 8 июля 1695, Нидерланды) Теория вероятностей и математическая
- 8. Теория вероятностей и математическая статистика. Введение Русский период в развитии теории вероятностей Особенно быстро теория вероятностей
- 9. Теория вероятностей и математическая статистика. Введение Пространство элементарных событий. Алгебра событий
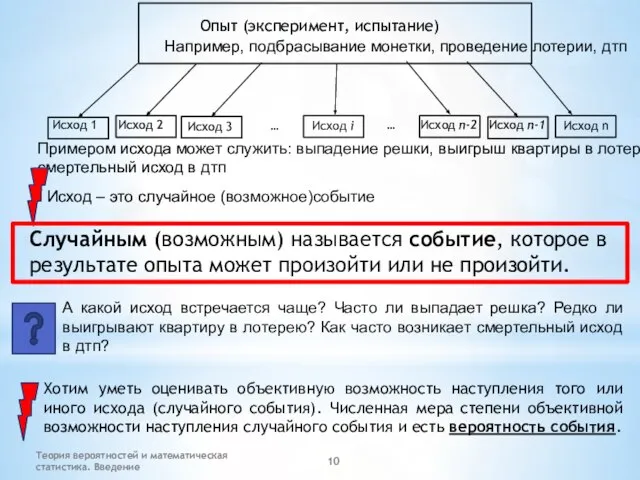
- 10. Теория вероятностей и математическая статистика. Введение Опыт (эксперимент, испытание) Например, подбрасывание монетки, проведение лотерии, дтп Исход
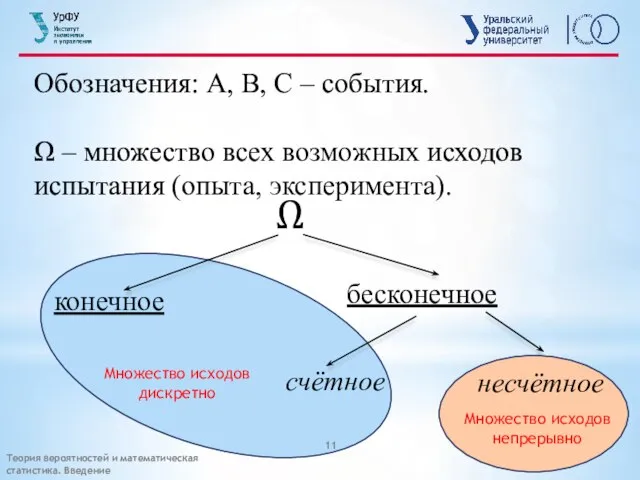
- 11. Обозначения: А, В, С – события. Ω – множество всех возможных исходов испытания (опыта, эксперимента). Ω
- 12. A⊂B Читается: А влечёт за собой В Теория вероятностей и математическая статистика. Введение
- 13. Теория вероятностей и математическая статистика. Введение Пример. А={выпала «2» на игральном кубике}; В={выпало чётное число на
- 14. Теория вероятностей и математическая статистика. Введение Если A⊂B и В⊂А, то А и В называются равносильными:
- 15. Теория вероятностей и математическая статистика. Введение События Совместные Несовместные
- 16. Теория вероятностей и математическая статистика. Введение Пример. События, состоящие в том, что в семье из двух
- 17. А Теория вероятностей и математическая статистика. Введение
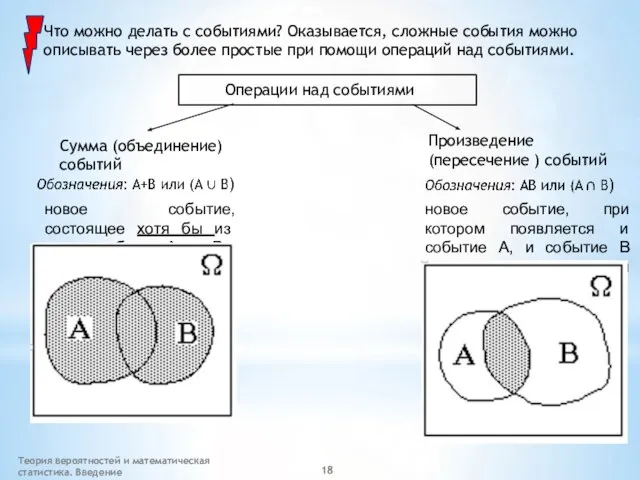
- 18. Теория вероятностей и математическая статистика. Введение Что можно делать с событиями? Оказывается, сложные события можно описывать
- 19. Теория вероятностей и математическая статистика. Введение Утверждение. АВ⊆А В
- 20. Теория вероятностей и математическая статистика. Введение
- 21. Теория вероятностей и математическая статистика. Введение Было изучено: события, как вспомогательный аппарат свойства событий
- 23. Скачать презентацию

















 Равенство фигур
Равенство фигур Некоторые ошибки интерпретации относительных величин
Некоторые ошибки интерпретации относительных величин Число 10
Число 10 Презентация на тему Площадь круга и кругового сектора
Презентация на тему Площадь круга и кругового сектора 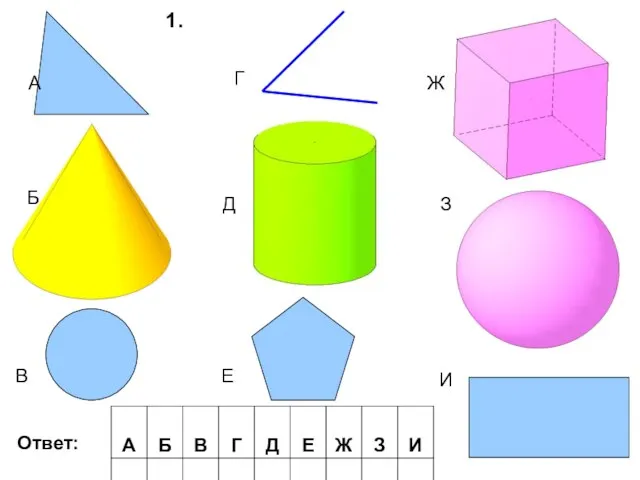 Геометрические тела. 5 класс
Геометрические тела. 5 класс Ортодромия и локсодромия
Ортодромия и локсодромия Окружность. (Задача 18. Вариант 105)
Окружность. (Задача 18. Вариант 105) Azərbaycan Dövlət Neft və Sənaye Universiteti Optimal Control
Azərbaycan Dövlət Neft və Sənaye Universiteti Optimal Control Формулы сокращённого умножения
Формулы сокращённого умножения Окружность и круг
Окружность и круг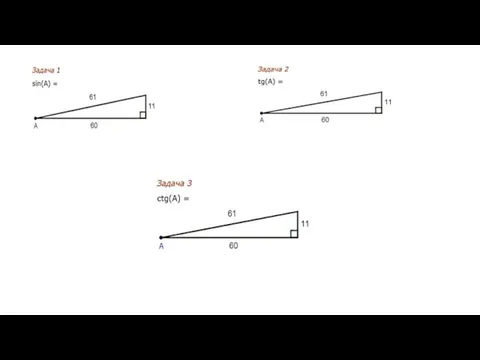 Решение примеров
Решение примеров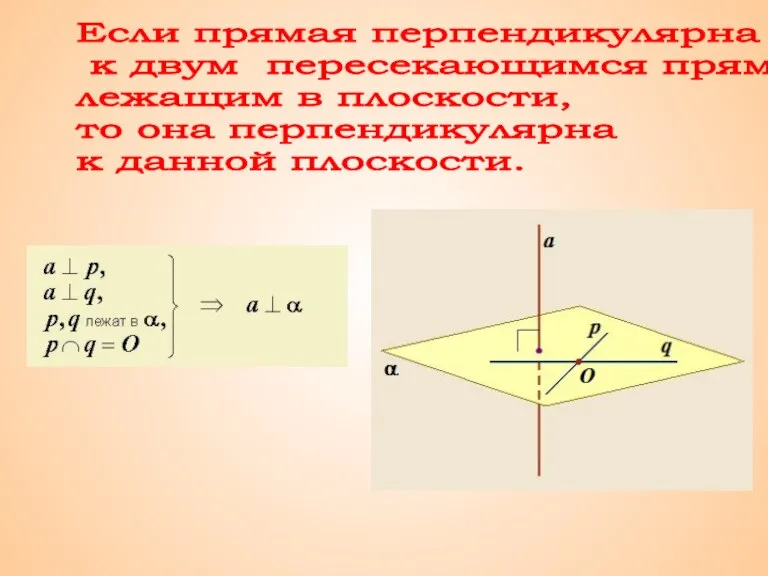 Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Учебно-методический комплект по математике по ФГОС второй ступени
Учебно-методический комплект по математике по ФГОС второй ступени Решение задач
Решение задач Очень жадный крокодил или больше, меньше, равно
Очень жадный крокодил или больше, меньше, равно Презентация на тему Степень числа. Квадрат и куб числа
Презентация на тему Степень числа. Квадрат и куб числа  Конусы в нашей жизни
Конусы в нашей жизни Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых (4 класс)
Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых (4 класс) Общие вопросы теории очередей
Общие вопросы теории очередей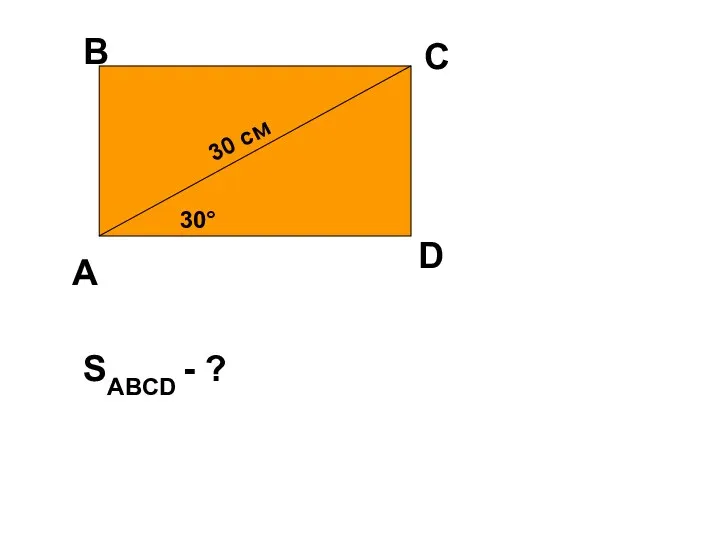 Параметры четырехугольника
Параметры четырехугольника Геометрия, 10 класс
Геометрия, 10 класс Дифференциалы высших порядков
Дифференциалы высших порядков Производная вокруг нас
Производная вокруг нас Параллелограмм
Параллелограмм Основное свойство пропорции
Основное свойство пропорции Математика и спорт
Математика и спорт Угол между прямой и плоскостью
Угол между прямой и плоскостью Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости