Математическая логика

Логика - наука о формах и способах мышления.
Он пытался первым найти ответ на вопрос
«Как мы рассуждаем?», изучал правила мышления. Аристотель впервые дал систематическое изложение логики.
Он подверг анализу человеческое мышление, его формы - понятие, суждение, умозаключение.
Так возникла формальная логика.
Основы логики были заложены работами ученого и философа Аристотеля
(384 -322гг. до н.э.).

Основные формы мышления:
Понятие – форма мышления, фиксирующая основные существенные признаки объекта.
Высказывание - это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть истинно или ложно.
Не являются высказываниями восклицательные и вопросительные предложения:
Высказывания делятся на:
простые
составные (истинность которых вычисляется с помощью алгебры высказываний)
Умозаключение – форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение)

Англичанин Джордж Буль (1815-1864, математик-самоучка), на фундаменте, заложенном Лейбницем, создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний). В его работах логика обрела свой алфавит, свою орфографию и грамматику.
Немецкий ученый Готфрид Лейбниц (1646-1716) заложил основы математической логики. Он пытался построить первые логические исчисления (свести логику к математике), предложил использовать символы вместо слов обычного языка, поставил много задач по созданию символьной логики, его идеи оказали влияние на последующие работы ученых в этой области.
Математическая логика

Алгебра логики (высказываний) работает с высказываниями.
Различают:
1. Логические константы (логические утверждения) – конкретные частные утверждения (И/Л)
2. Логические переменные (предикаты) – логические высказывания, значения которых меняются в зависимости от входящих в них переменных, обозначаются заглавными латинскими буквами А, В, С, D, F,…
Истинному высказыванию ставится в соответствие 1, ложному — 0.

3. Логические функции ( логические формулы) – сложные логические выражения образованные из простых и связанные логическими операциями И, ИЛИ, НЕ и др.)
Высказывание “Все мышки и кошки с хвостами”
является сложным и состоит из двух простых высказываний.
А=“Все мышки с хвостами” и В=“Все кошки с хвостами”
Его можно записать в виде логической функции, значение которой истинно: F(A,B)=A и B
В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только ложно (0) или истинно (1).

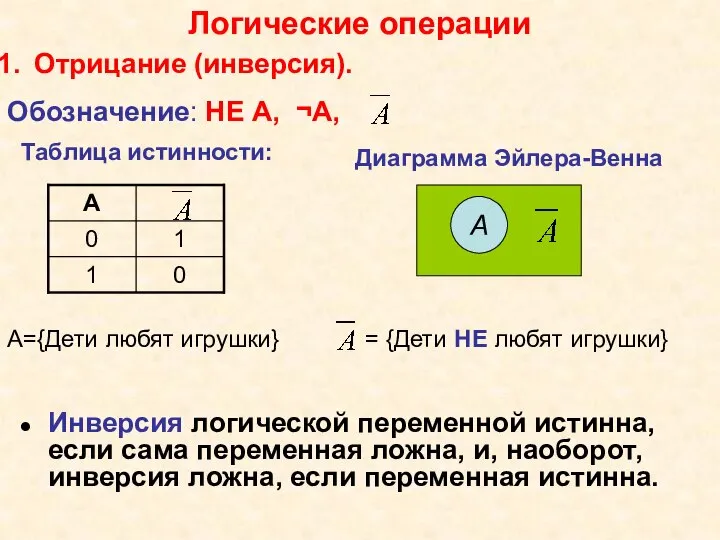
Логические операции
Отрицание (инверсия).
Обозначение: НЕ А, ¬А,
А={Дети любят игрушки} = {Дети НЕ любят игрушки}
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.

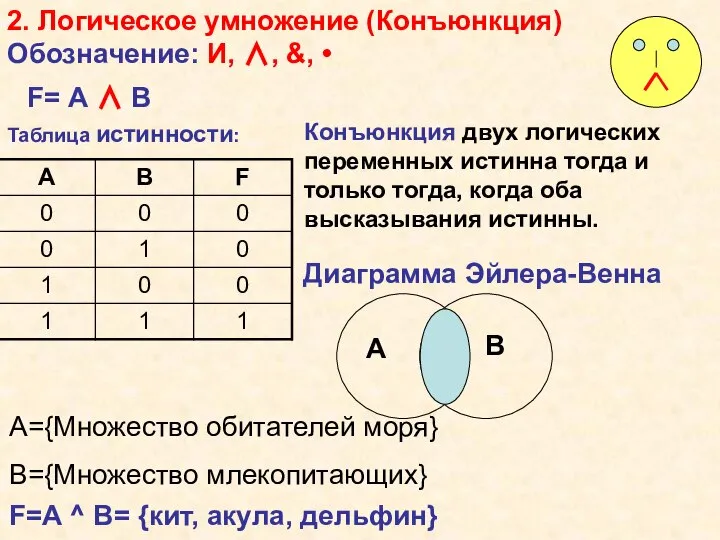
2. Логическое умножение (Конъюнкция) Обозначение: И, ∧, &, •
F=A ^ B= {кит, акула, дельфин}
Таблица истинности:
F= А ∧ В
Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания истинны.

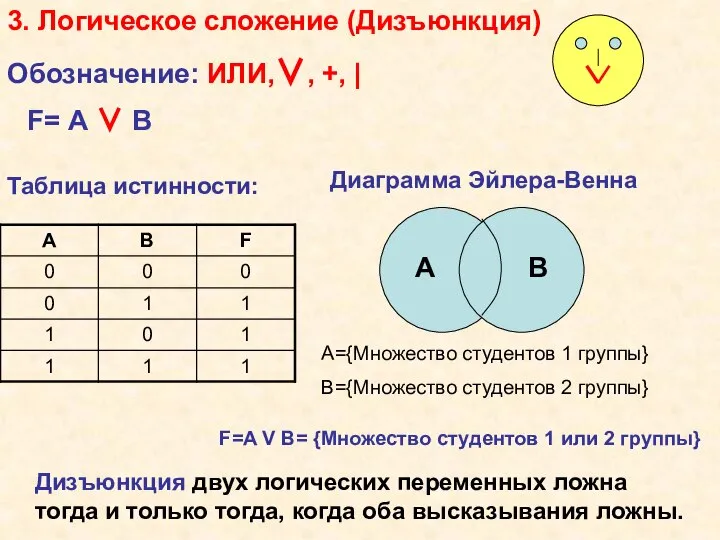
3. Логическое сложение (Дизъюнкция)
Обозначение: ИЛИ,∨, +, |
F=A V B= {Множество студентов 1 или 2 группы}
Таблица истинности:
F= А ∨ В
Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны.

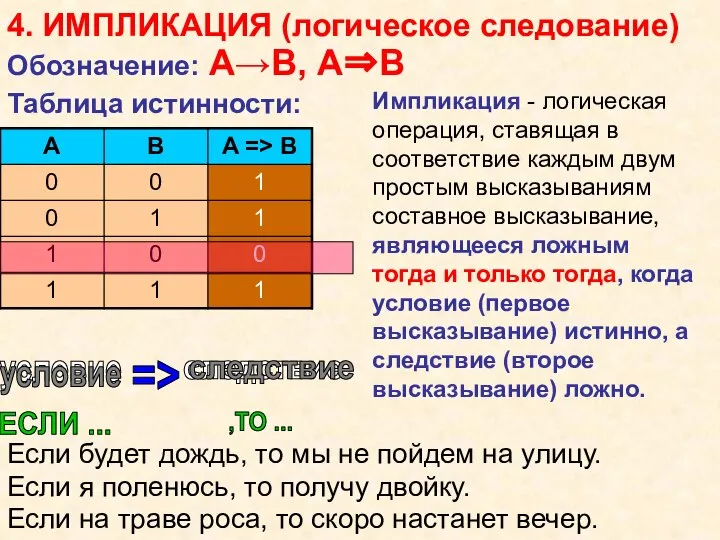
4. ИМПЛИКАЦИЯ (логическое следование)
условие
следствие
ЕСЛИ ...
,ТО ...
=>
условие
следствие
Если будет дождь, то мы не пойдем на улицу.
Если я поленюсь, то получу двойку.
Если на траве роса, то скоро настанет вечер.
Обозначение: А→В, А⇒В
Таблица истинности:
Импликация - логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

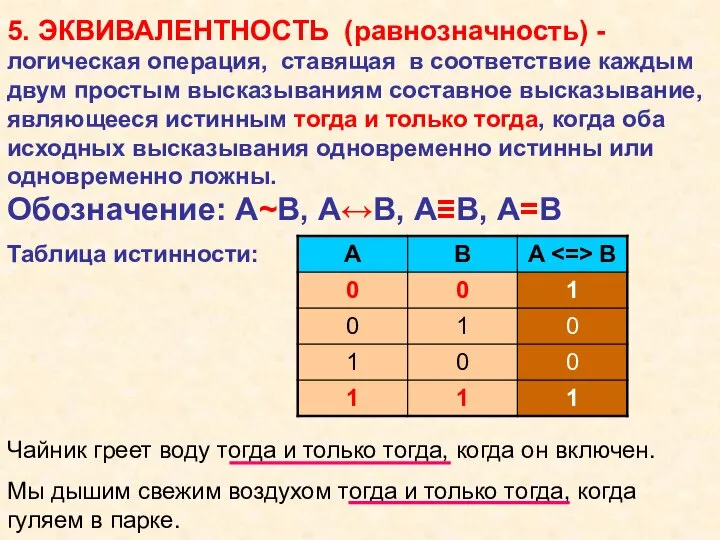
5. ЭКВИВАЛЕНТНОСТЬ (равнозначность) -
Чайник греет воду тогда и только тогда, когда он включен.
Мы дышим свежим воздухом тогда и только тогда, когда гуляем в парке.
Обозначение: А~В, А↔В, А≡В, А=В
логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Таблица истинности:

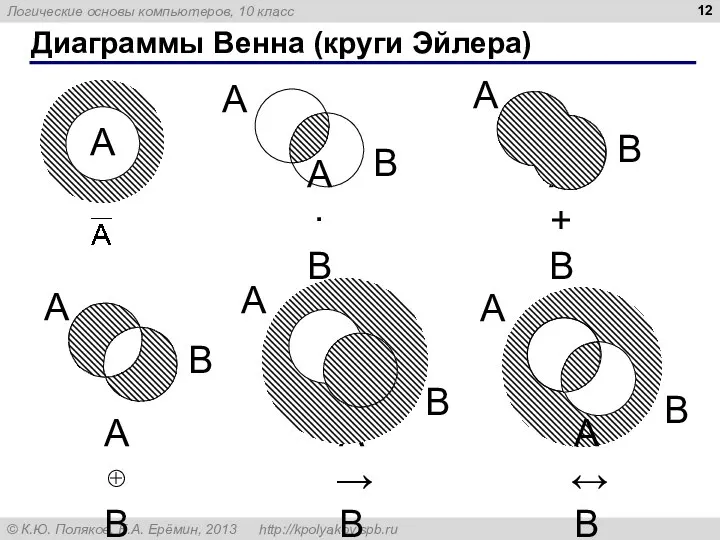
Диаграммы Венна (круги Эйлера)
A·B
A+B
A⊕B
A→B
A↔B

Приоритет логических операций:
() Операции в скобках
НЕ Отрицание
И логическое умножение
ИЛИ Логическое сложение
→ Импликация
↔ Эквивалентность

Вычисление логических выражений
Пример1.
Вычислить значение логического выражения
«(2·2=5 или 2·2=4) и (2·2 ≠ 5 или 2·2 ≠ 4)»
Обозначим
А=«2·2=5» – ложно (0)
В=«2·2=4» – истинно (1)
Тогда (А или В) и ( или )

Задание 2. Определите истинность составного высказывания
состоящего из простых высказываний:
А={Принтер – устройство вывода информации}
В={Процессор – устройство хранения информации}
C={Монитор – устройство вывода информации}
D={Клавиатура – устройство обработки информации}
Определяем истинность составного высказывания:
А=1, В=0, С=1, D=0
Установим истинность простых высказываний:

ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ
ПО ЛОГИЧЕСКОМУ ВЫРАЖЕНИЮ
Таблицу, показывающую, какие значения принимает сложное высказывание при всех сочетаниях значений входящих в него простых высказываний (переменных), называют таблицей истинности сложного высказывания ( логической формулы).
По формуле логической функции легко рассчитать ее таблицу истинности, соблюдая приоритет логических операций и действия в скобках

Порядок действий:
Количество строк в таблице Q=2n, где n - количество переменных (аргументов), здесь n = 3 (А, В, С) и тогда Q=23=8
2. Количество столбцов = число переменных + число операций (здесь 3+3=6 столбцов)
3. Выписать наборы входных переменных. Это удобнее сделать так:
разделить колонку значений первой переменной пополам и заполнить верхнюю половину 0, нижнюю половину 1.
разделить колонку значений второй переменной на 4 части и заполнить каждую четверть чередующимися группами 0 и 1 , начиная опять с группы 0.
продолжить деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами из 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа. (Можно заполнять все колонки, начиная с группы единиц.)
4. Провести заполнение таблицы истинности по столбикам, выполняя логические операции.
Пример. Построим таблицу истинности следующей функции:

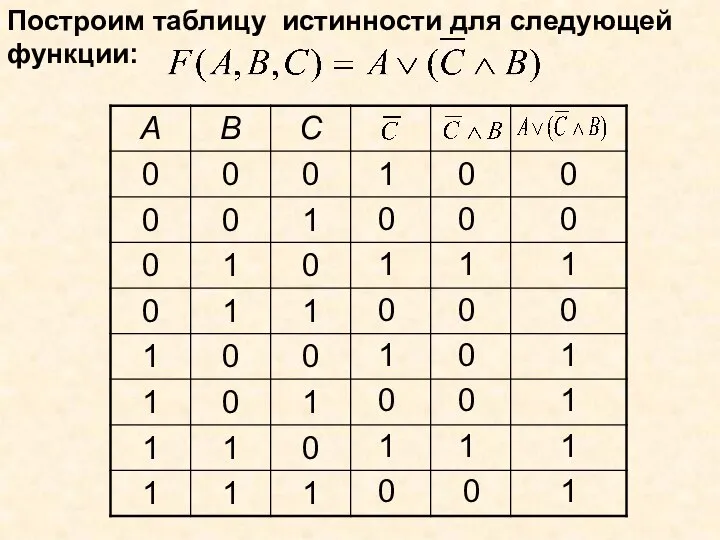
Построим таблицу истинности для следующей функции:
1
1
1
1
0
0
0
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
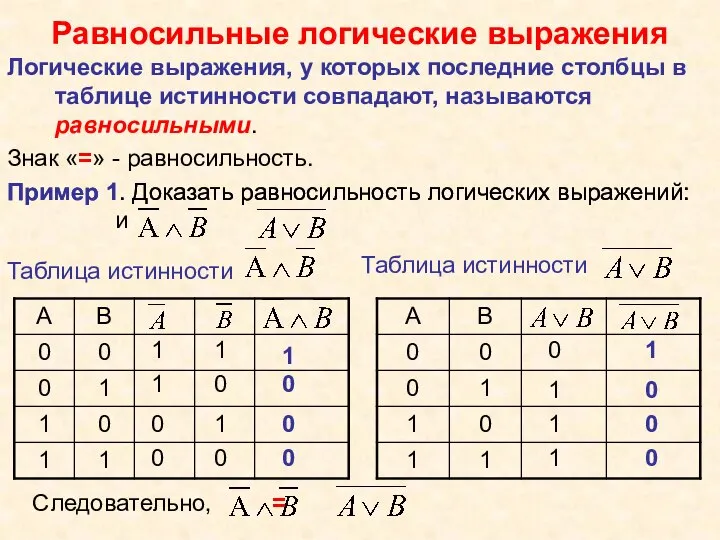
1
1

Пример 1. Доказать равносильность логических выражений: и
Равносильные логические выражения
Логические выражения, у которых последние столбцы в таблице истинности совпадают, называются равносильными.
Знак «=» - равносильность.
0
1
1
1
1
0
1
0
0
0
0
0
0
1
1
1
1
0
0
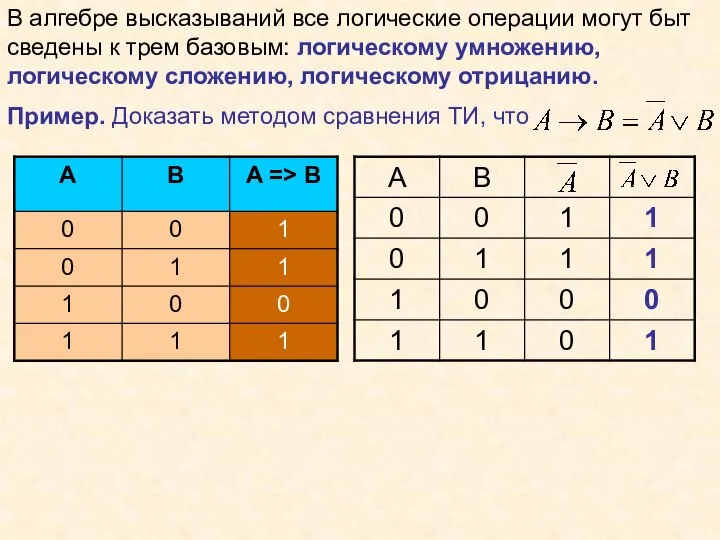
0

В алгебре высказываний все логические операции могут быт сведены к трем базовым: логическому умножению, логическому сложению, логическому отрицанию.
Пример. Доказать методом сравнения ТИ, что

Законы алгебры логики и свойства логических операций
используются для упрощения логических выражений
(минимизации логических функций)