РўР’РёРњРЎ_Лекция 4_Дискретные СЃРучайные РІРµРичины

Лекция 4. Дискретные случайные величины
Возможности использования понятия «случайное событие» являются ограниченными. Это связано с тем, что элементарные исходы эксперимента в общем случае имеют нечисловую (качественную) природу, а интерес, как правило, представляет их количественная характеристика, отражающая в каждом конкретном случае, например, размер выигрыша.
Для того чтобы качественные результаты эксперимента отобразить количественно, достаточно каждому элементарному исходу эксперимента (событию) ω сопоставить некоторое число, т.е. на множестве всех элементарных исходов эксперимента Ω задать функцию.
Пролог

Определение 1. Случайной величиной X называется функция f, заданная на множестве Ω элементарных исходов эксперимента, т.е.
Итак, случайной величиной называется величина, которая в результате эксперимента в зависимости от случая принимает одно из своих возможных значений.
Определение 2. Законом распределения случайной величины X называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Лекция 4. Дискретные случайные величины
§1. Закон распределения СВ

В зависимости от множества Ω различают дискретные и непрерывные случайные величины.
Определение 3. Дискретной называется случайная величина у которой множество элементарных исходов эксперимента конечное или счётное.
Закон распределения такой величины может быть представлен таблично, аналитически или графически.
Определение 4. Под непрерывной понимают случайную величину у которой множество элементарных исходов эксперимента представляет собой интервал (континуальное множество).
Задать закон распределения такой величины представить таблично уже нельзя.
§1. Закон распределения СВ
Лекция 4. Дискретные случайные величины

Простейшей формой закона распределения дискретной случайной величины (ДСВ) является таблица, в которой в порядке возрастания перечислены возможные значения случайной величины и соответствующие им вероятности.
Все возможные значения случайной величины X образуют полную группу событий. Поэтому их сумма является достоверным событием, а, значит, вероятность такого события равна единице.
§1. Закон распределения СВ
Лекция 4. Дискретные случайные величины

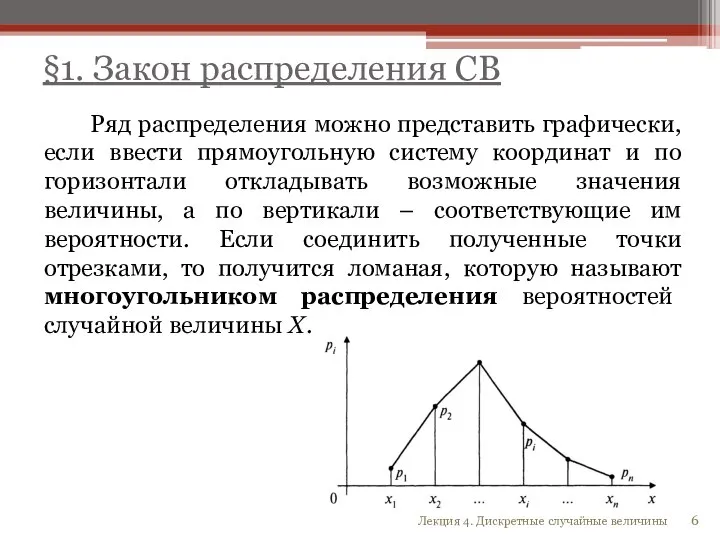
Ряд распределения можно представить графически, если ввести прямоугольную систему координат и по горизонтали откладывать возможные значения величины, а по вертикали – соответствующие им вероятности. Если соединить полученные точки отрезками, то получится ломаная, которую называют многоугольником распределения вероятностей случайной величины Х.
§1. Закон распределения СВ
Лекция 4. Дискретные случайные величины

Определение 5. ДСВ имеет биномиальный закон распределения с параметрами n и p, если она принимает значения 0, 1, 2, …, n, вероятности которых определяются по формуле Бернулли:
где 0 < p < 1, q = 1 - p.
Ряд распределения имеет вид:
Введённое определение корректно, так как сумма вероятностей pi – это сумма коэффициентов бинома:
§2. Биномиальное распределение
Лекция 4. Дискретные случайные величины

Пример 1
Эксперимент: выбрать наугад деталь для проверки
качества.
Событие А: выбрана бракованная деталь.
n=5 – число выбранных для проверки деталей (число всех проведённых экспериментов).
Величина Х: число бракованных деталей среди отобранных на проверку.
8
Лекция 4. Дискретные случайные величины

§3. Распределение Пуассона
9
Определение 6. ДСВ распределена по закону Пуассона с параметром λ>0, если она принимает счётное множество значений 0,1,2,…,m,…, вероятности которых определяются по формуле:
Ряд распределения имеет вид:
Введённое определение корректно, так как:
Лекция 4. Дискретные случайные величины

Определение 7. ДСВ имеет геометрическое распределение с параметром p, если она принимает счётное множество значений 1,2,…,m,… c вероятностями
где 0 < p < 1, q = 1 - p.
Ряд распределения имеет вид:
Введённое определение корректно, так как:
Величина Х есть число испытаний m, проведённых по схеме Бернулли до первого наступления события А и в каждом испытании P(A) = p.
§4. Геометрическое распределение
Лекция 4. Дискретные случайные величины

Пример 2
Эксперимент: выбрать наугад деталь для проверки
качества.
Событие А: выбрана бракованная деталь.
n – число выбранных для проверки деталей – не ограничено.
Величина Х: число проверенных деталей до первого обнаружения бракованной детали.
11
Лекция 4. Дискретные случайные величины

Определение 8.
ДСВ имеет гипергеометрическое распределение с параметрами n, M, N, если она принимает значения
0, 1, 2, …, m, …, min{n, M} c вероятностями
где M ≤ N, n ≤ N; n, M, N – натуральные числа.
Величина Х есть число объектов m, обладающих заданным свойством, среди n объектов, случайно отобранных (без повторов) из совокупности N объектов, из которых M обладают этим свойством.
§5. Гипергеометрическое распределение
Лекция 4. Дискретные случайные величины

Пример 3
Эксперимент: выбрать наугад деталь для проверки
качества.
N=10 – число всех деталей в партии (объектов);
M=4 – число бракованных деталей в партии (объектов, обладающих заданным свойством);
n=3 – число деталей, отобранных для проверки качества.
Величина Х: число бракованных деталей среди отобранных для проверки качества.
13
Лекция 4. Дискретные случайные величины

Определение 9.
Две случайные величины называются независимыми, если закон распределения одной не зависит от того, какие значения принимает другая.
В противном случае случайные величины называют зависимыми.
Для случайных величин определены следующие математические операции:
умножение на постоянную величину;
возведение в степень;
сложение величин;
вычитание величин;
умножение величин.
§6. Математические операции над СВ
Лекция 4. Дискретные случайные величины

Определение 10. Произведением случайной величины Х и постоянной величины k называется случайная величина k⋅X, которая принимает значения k⋅xi с вероятностями pi.
X:
Y=2Х:
§6. Математические операции над СВ
Пример 4
Лекция 4. Дискретные случайные величины

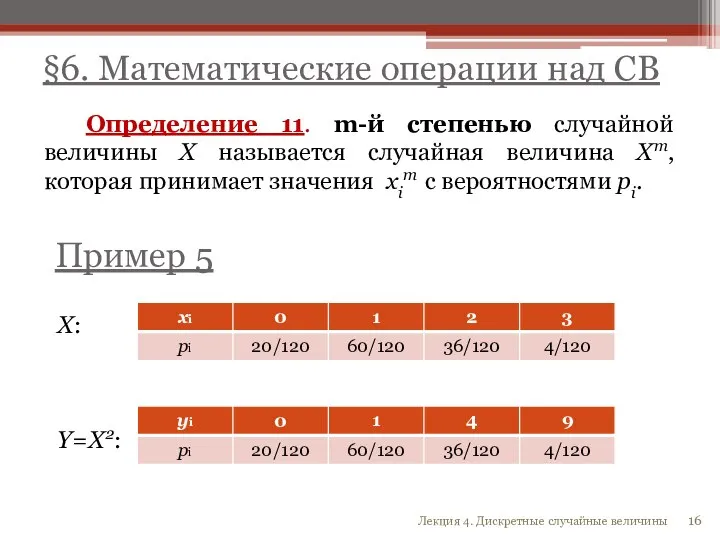
Определение 11. m-й степенью случайной величины Х называется случайная величина Xm, которая принимает значения xim с вероятностями pi.
X:
Y=Х2:
§6. Математические операции над СВ
Пример 5
Лекция 4. Дискретные случайные величины

Определение 12. Суммой случайных величин
Х и Y называется случайная величина X+Y, которая принимает значения xi + yj с вероятностями
pij = P(X= xi, Y= yj), где i=1, 2, …, n; j=1, 2, …, m.
Для независимых величин Х и Y: pij =P(X= xi)⋅P(Y= yj).
X:
Y:
Z=X+Y:
17
§6. Математические операции над СВ
Пример 6
Лекция 4. Дискретные случайные величины

Определение 13. Разностью случайных величин
Х и Y называется случайная величина X-Y, которая принимает значения xi - yj с вероятностями
pij = P(X= xi, Y= yj), где i=1, 2, …, n; j=1, 2, …, m.
Для независимых величин Х и Y: pij =P(X= xi)⋅P(Y= yj).
X:
Y:
Z=X-Y:
§6. Математические операции над СВ
Пример 7
Лекция 4. Дискретные случайные величины

Определение 14. Произведением случайных величин Х и Y называется случайная величина X⋅Y, которая принимает значения xi ⋅ yj с вероятностями
pij = P(X= xi, Y= yj), где i=1, 2, …, n; j=1, 2, …, m.
Для независимых величин Х и Y: pij =P(X= xi)⋅P(Y= yj).
X:
Y:
Z=X⋅Y:
§6. Математические операции над СВ
Пример 8
Лекция 4. Дискретные случайные величины