Содержание
- 2. Логические выражения Логическое выражение — это выражение, результат вычисления которого — логическое значение (истина или ложь).
- 3. Порядок вычисления скобки НЕ И ИЛИ импликация эквиваленция 1 2 3 4 5 6 , исключающее
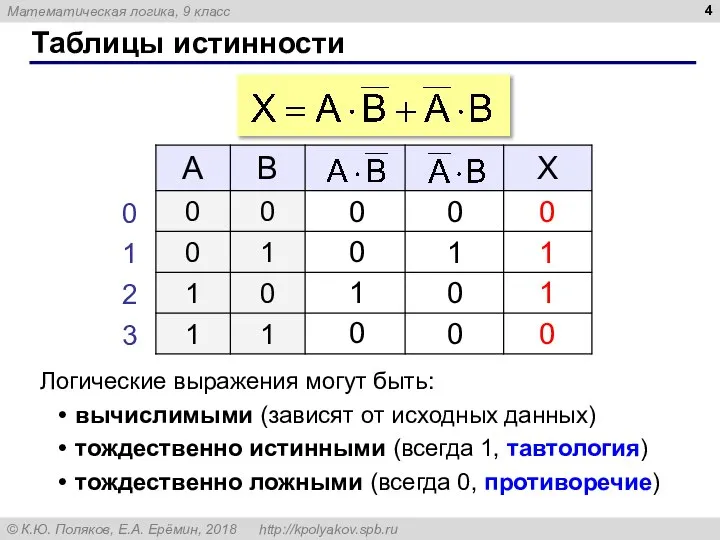
- 4. Таблицы истинности Логические выражения могут быть: вычислимыми (зависят от исходных данных) тождественно истинными (всегда 1, тавтология)
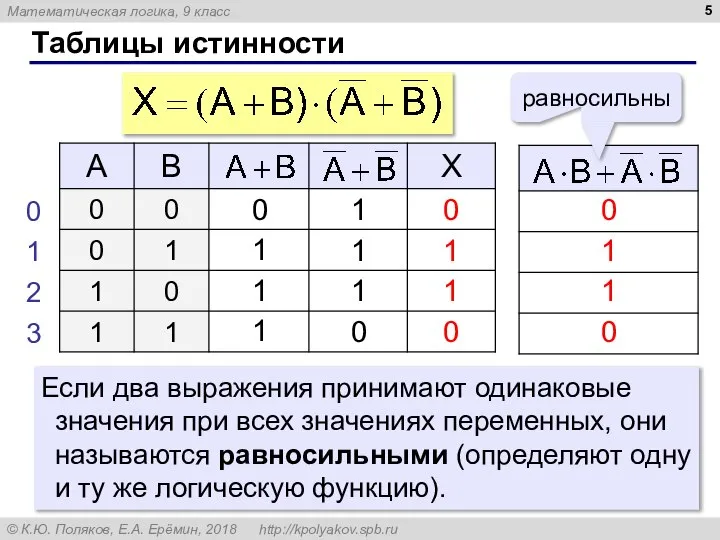
- 5. Таблицы истинности Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными (определяют
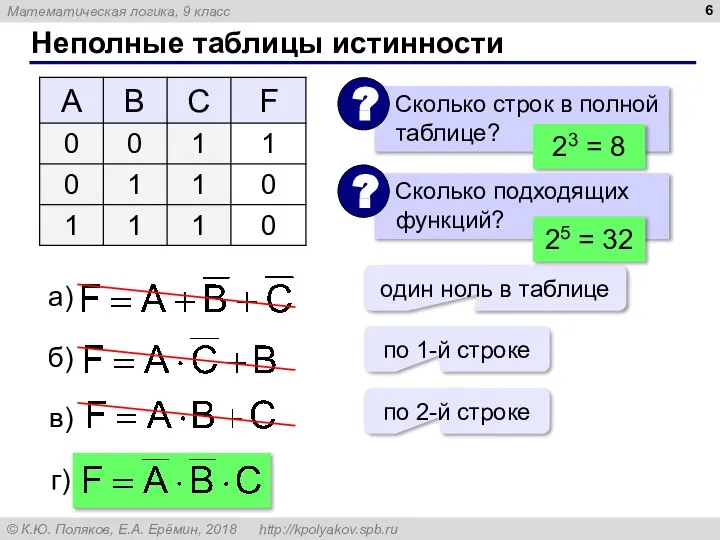
- 6. Неполные таблицы истинности 23 = 8 один ноль в таблице по 1-й строке по 2-й строке
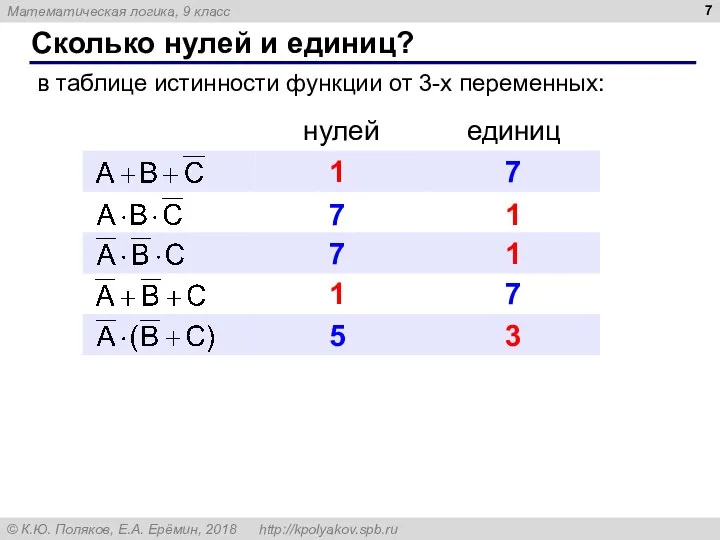
- 7. Сколько нулей и единиц? в таблице истинности функции от 3-х переменных: 1 7 7 1 7
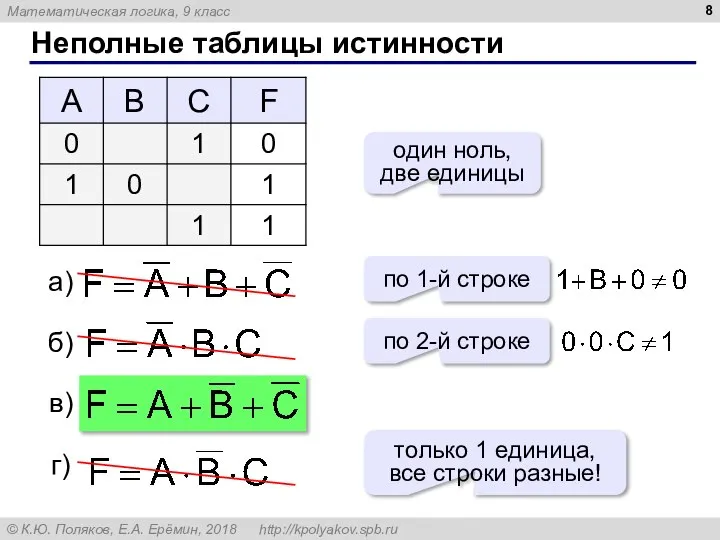
- 8. Неполные таблицы истинности один ноль, две единицы по 1-й строке по 2-й строке только 1 единица,
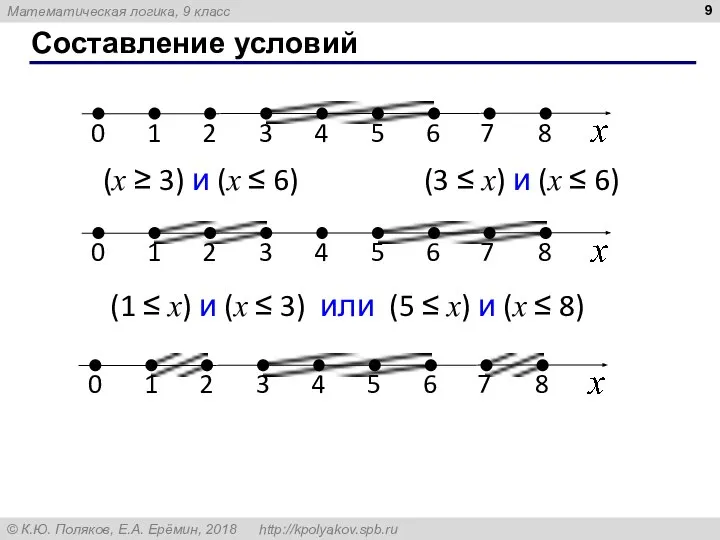
- 9. Составление условий (x ≥ 3) и (x ≤ 6) (3 ≤ x) и (x ≤ 6)
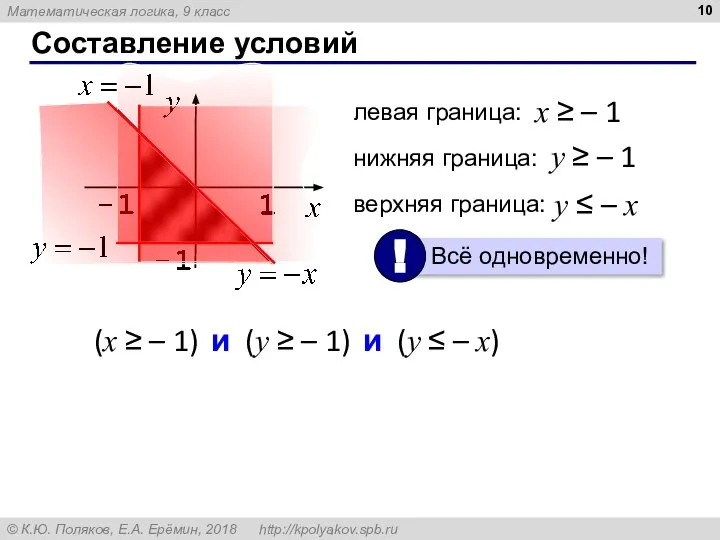
- 10. Составление условий левая граница: x ≥ – 1 нижняя граница: y ≥ – 1 верхняя граница:
- 11. Составление условий (x2+y2 ≤ 1) и (x ≤ 0) (x ≥ 0) и (x2+y2 ≤ 1)
- 13. Скачать презентацию



 Прямая и плоскость в пространстве
Прямая и плоскость в пространстве Решение задач
Решение задач Простейшие геометрические уравнения
Простейшие геометрические уравнения Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников Обработка экспериментальных данных. Описательная статистика: основные понятия
Обработка экспериментальных данных. Описательная статистика: основные понятия Окружность и её элементы
Окружность и её элементы Формулы двойного угла
Формулы двойного угла Экскурсия в мир чисел
Экскурсия в мир чисел Параллельные прямые в пространстве
Параллельные прямые в пространстве Действительный анализ. Интеграл Римана и критерий Лебега
Действительный анализ. Интеграл Римана и критерий Лебега Сфера
Сфера Многогранники
Многогранники Определенный интеграл. Пример 2. Лекция
Определенный интеграл. Пример 2. Лекция Логарифмические уравнения (часть 2)
Логарифмические уравнения (часть 2) Правила комбинаторики. Практическое занятие
Правила комбинаторики. Практическое занятие Презентация на тему Теорема Фалеса
Презентация на тему Теорема Фалеса  Смежные углы
Смежные углы Занимательная математика
Занимательная математика Системы линейных уравнений
Системы линейных уравнений Применение интеграла в физике и геометрии
Применение интеграла в физике и геометрии Сумма углов в треугольнике
Сумма углов в треугольнике Логика и математическая логика. История логики. Алгебра высказываний
Логика и математическая логика. История логики. Алгебра высказываний Сложение и вычитание дробей
Сложение и вычитание дробей Правильные многогранники
Правильные многогранники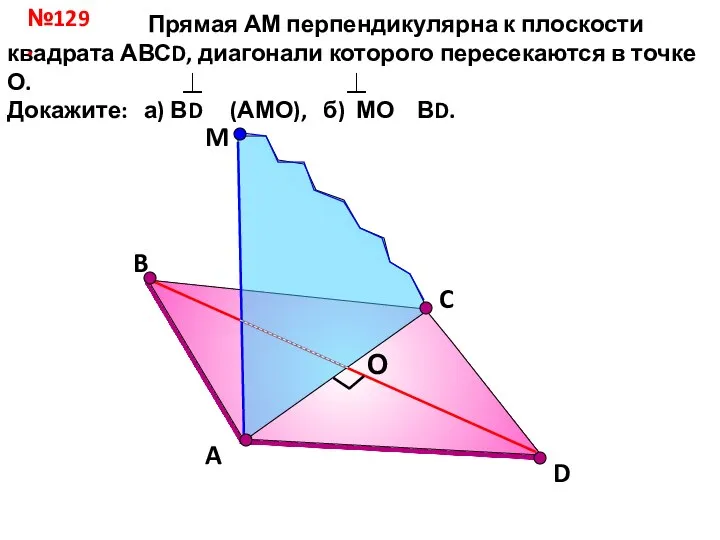 Прямая АМ перпендикулярна к плоскости квадрата АВСD. урок 29
Прямая АМ перпендикулярна к плоскости квадрата АВСD. урок 29 Сложение вида +2, +3
Сложение вида +2, +3 Презентация по математике "Основы концепции “глубинного анализа текстов" -
Презентация по математике "Основы концепции “глубинного анализа текстов" -  Учимся писать цифры
Учимся писать цифры