Содержание
- 2. Содержание Основные понятия Демонстрация сечений Метод следов Метод вспомогательных сечений Комбинированный метод Тест Защита проектов
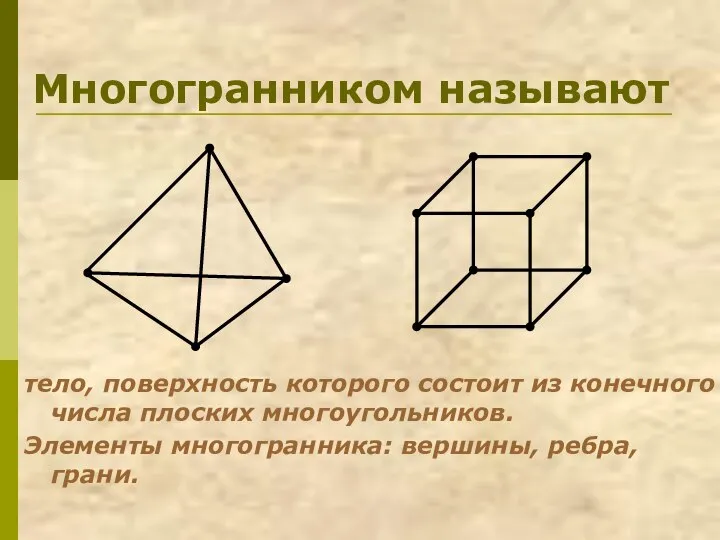
- 3. Многогранником называют тело, поверхность которого состоит из конечного числа плоских многоугольников. Элементы многогранника: вершины, ребра, грани.
- 4. Сечением поверхности геометрических тел называется плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки,
- 5. сечение
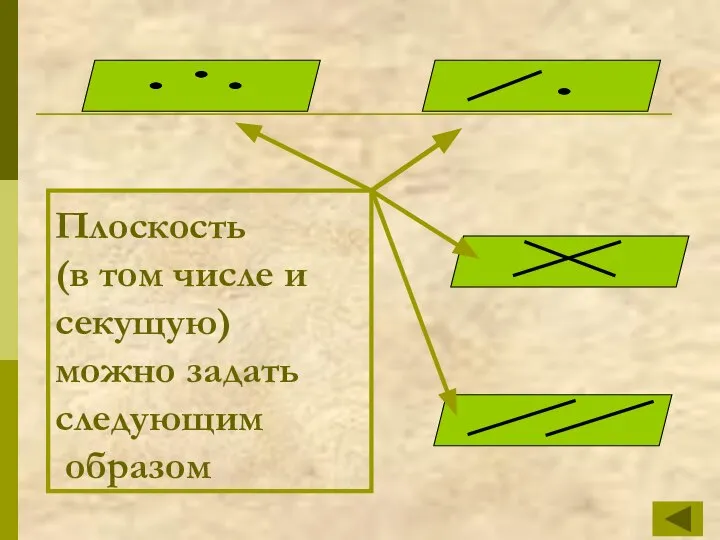
- 6. Плоскость (в том числе и секущую) можно задать следующим образом
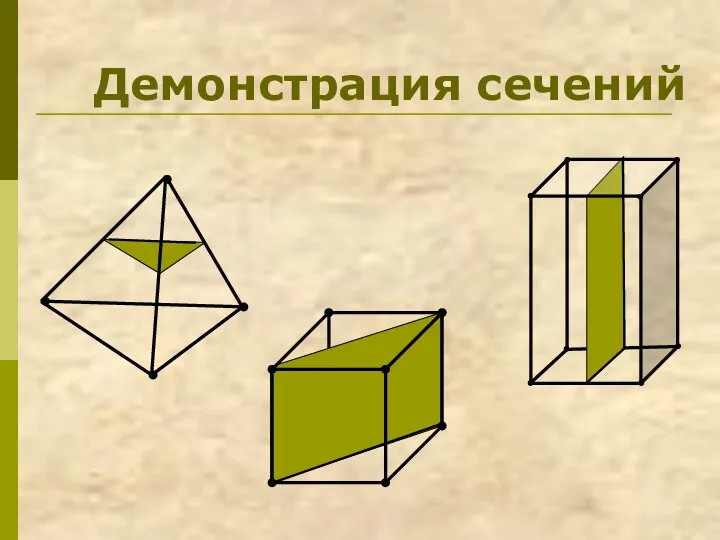
- 7. Демонстрация сечений
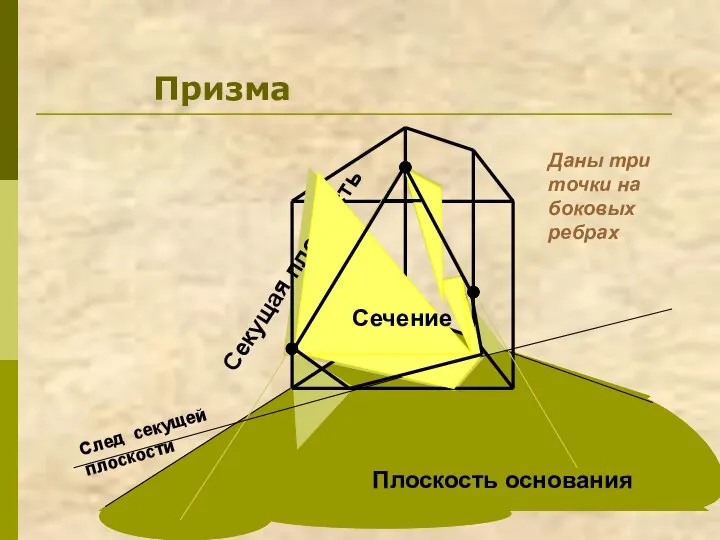
- 8. Призма Плоскость основания Секущая плоскость Даны три точки на боковых ребрах Сечение
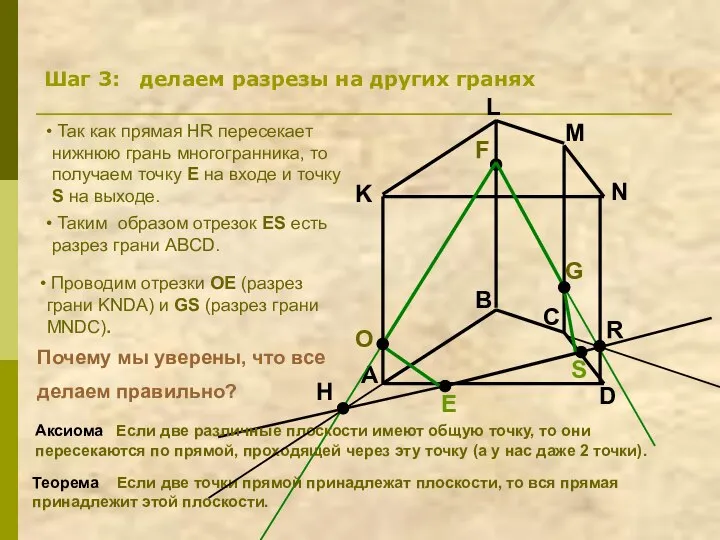
- 9. Секущая плоскость пересекает грани многогранника по прямым, а точнее по отрезкам - разрезам. Так как секущая
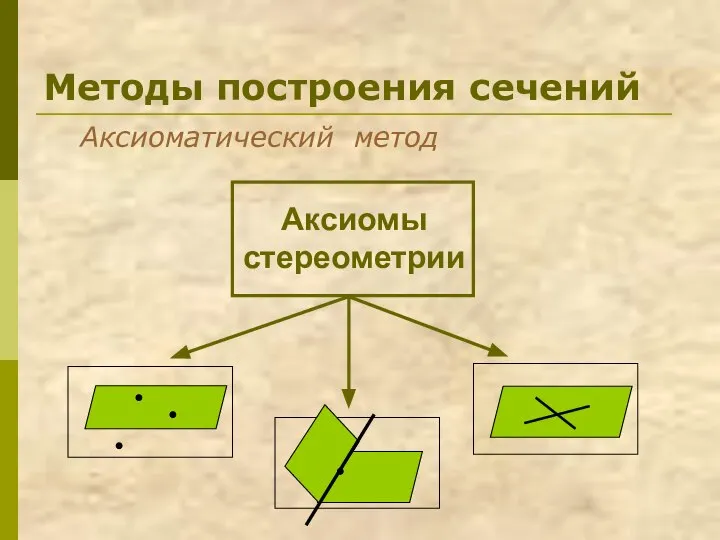
- 10. Методы построения сечений Аксиоматический метод Аксиомы стереометрии
- 11. Аксиоматический метод Метод следов Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей
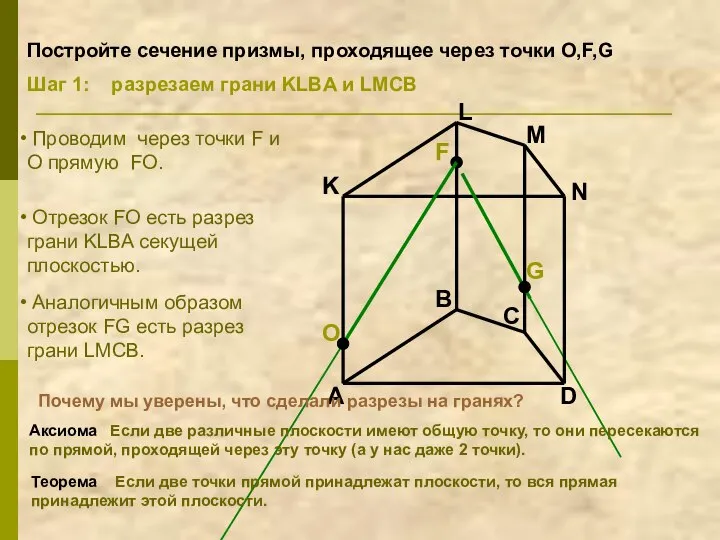
- 12. A B C D K L M N F G Проводим через точки F и O
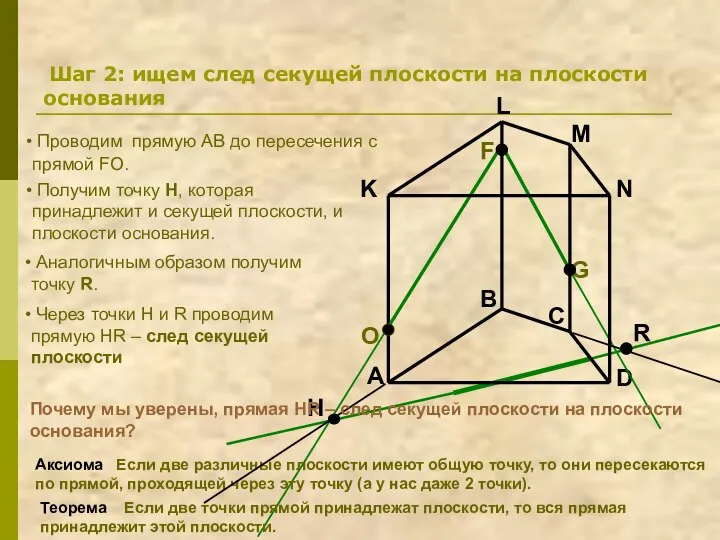
- 13. A B C D K L M N F G Шаг 2: ищем след секущей плоскости
- 14. A B C D K L M N F G Шаг 3: делаем разрезы на других
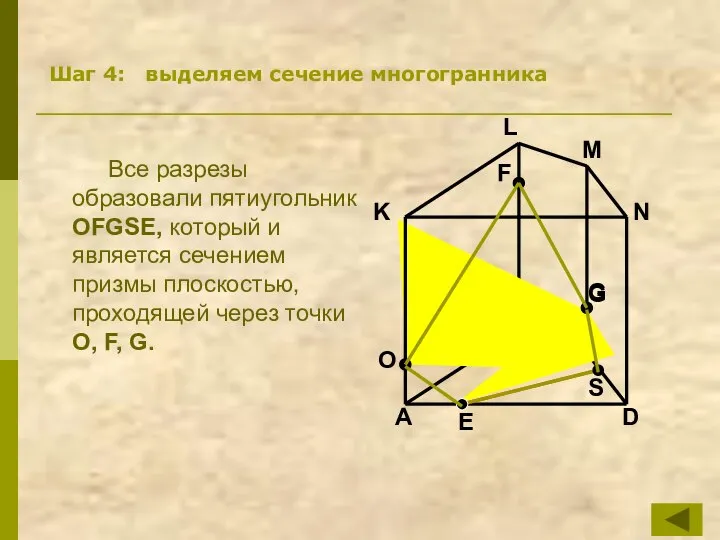
- 15. C B A D K L M N F G Шаг 4: выделяем сечение многогранника Все
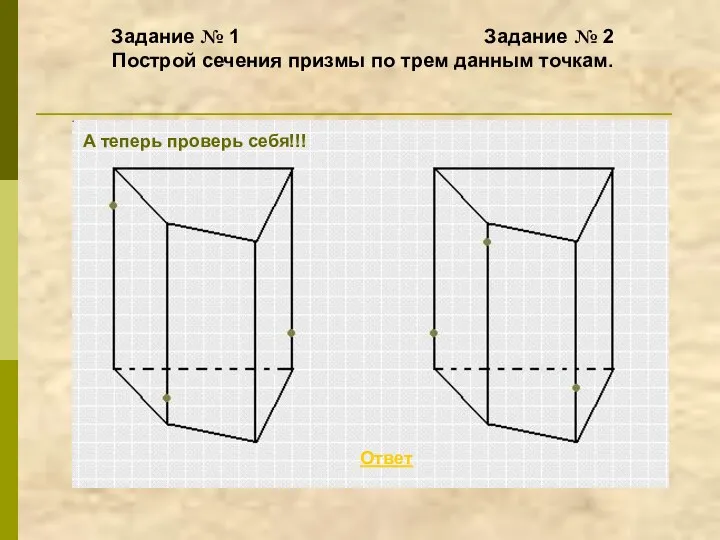
- 16. Задание № 1 Задание № 2 Построй сечения призмы по трем данным точкам. Ответ А теперь
- 17. Метод вспомогательных сечений Этот метод построения сечений многогранников является в достаточной мере универсальным. В тех случаях,
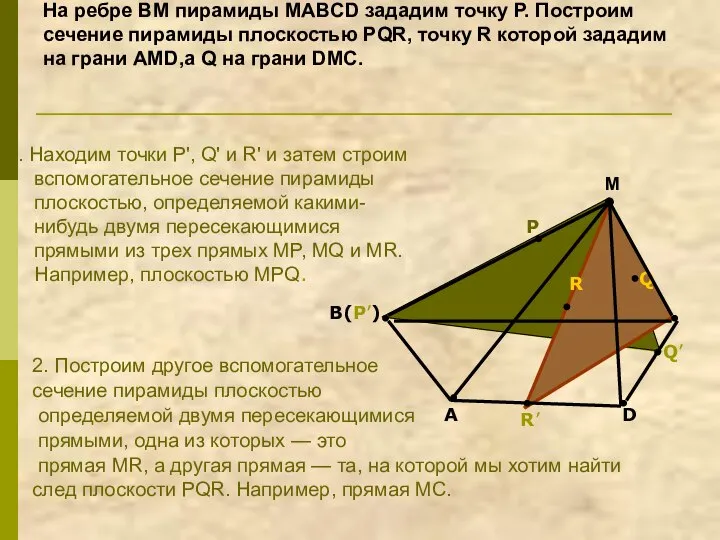
- 18. На ребре BM пирамиды MABCD зададим точку Р. Построим сечение пирамиды плоскостью PQR, точку R которой
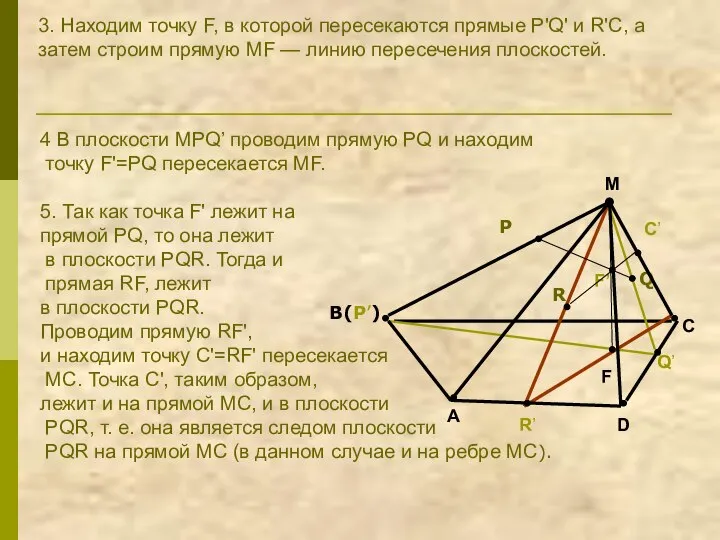
- 19. 3. Находим точку F, в которой пересекаются прямые Р'Q' и R'С, а затем строим прямую MF
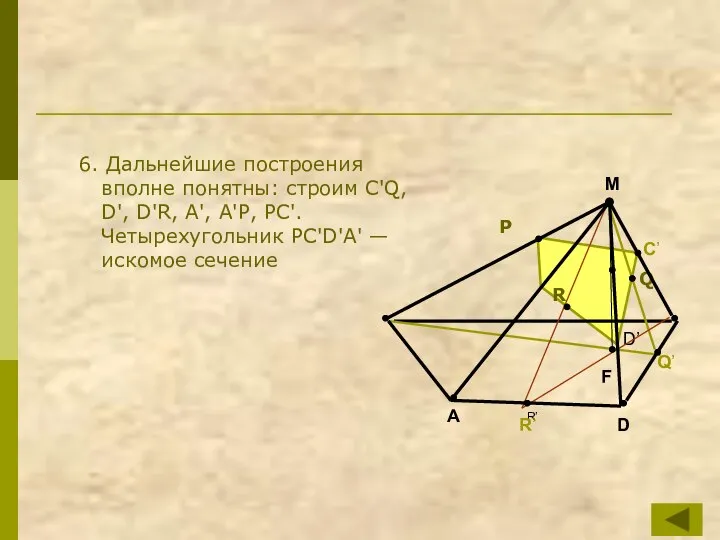
- 20. 6. Дальнейшие построения вполне понятны: строим C'Q, D', D'R, А', А'Р, РС'. Четырехугольник РС'D'А' — искомое
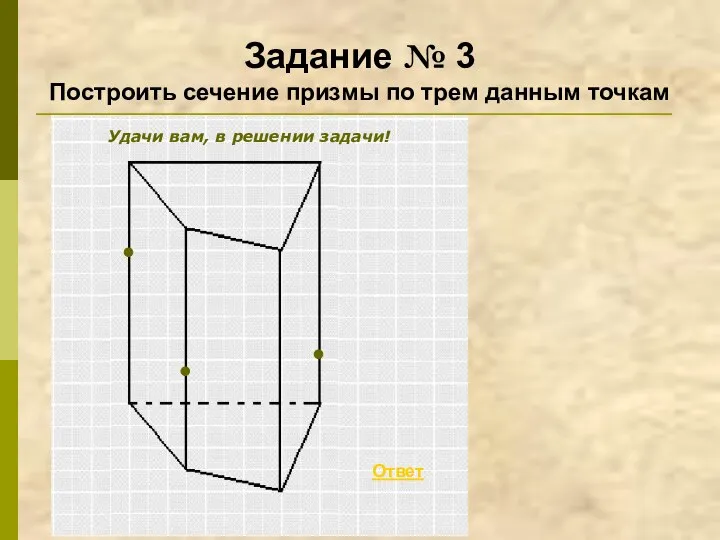
- 21. Задание № 3 Построить сечение призмы по трем данным точкам Ответ Удачи вам, в решении задачи!
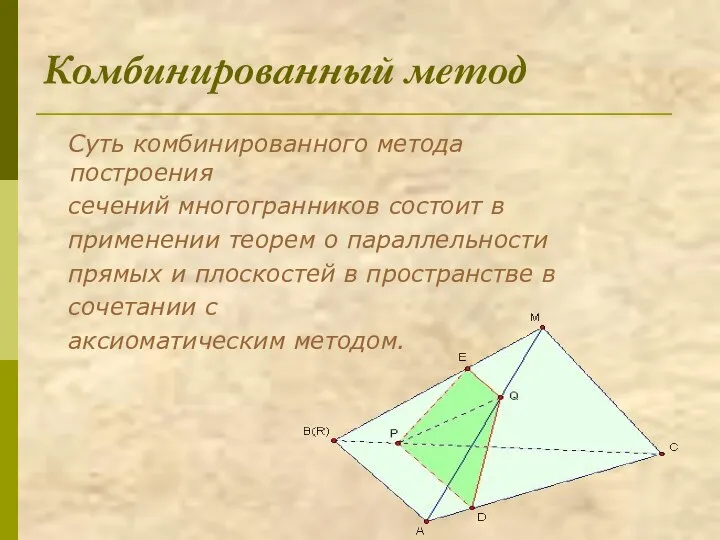
- 22. Комбинированный метод Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и
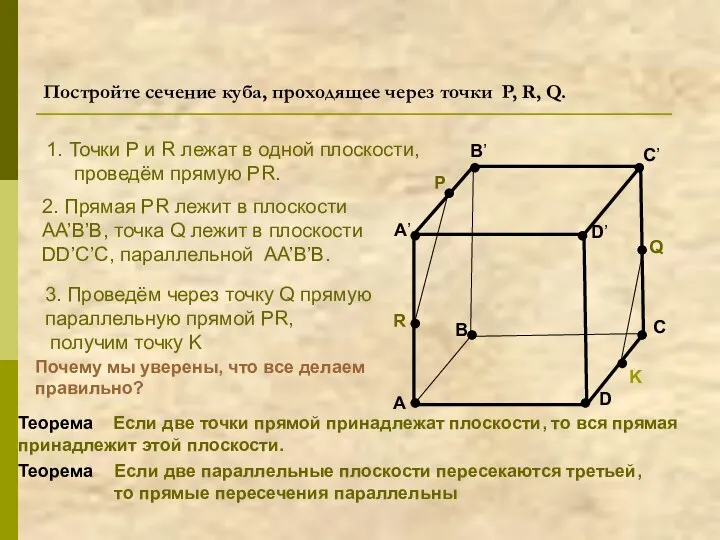
- 23. Постройте сечение куба, проходящее через точки P, R, Q. A B C D A’ B’ C’
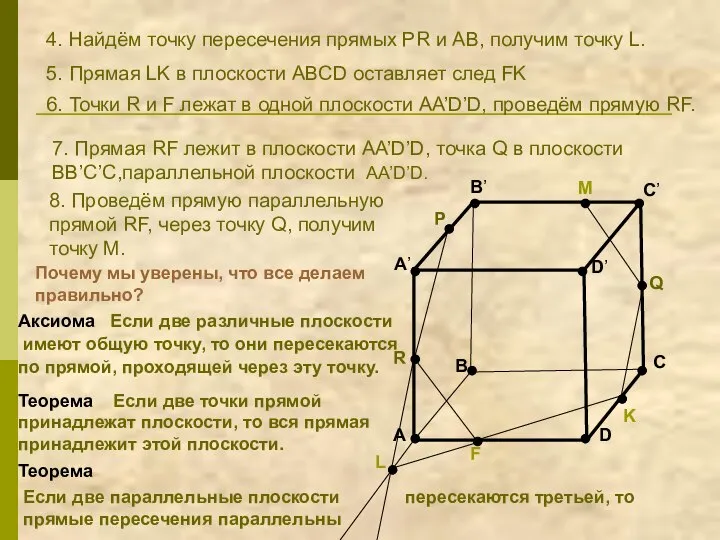
- 24. A B C D A’ B’ C’ D’ R P Q 4. Найдём точку пересечения прямых
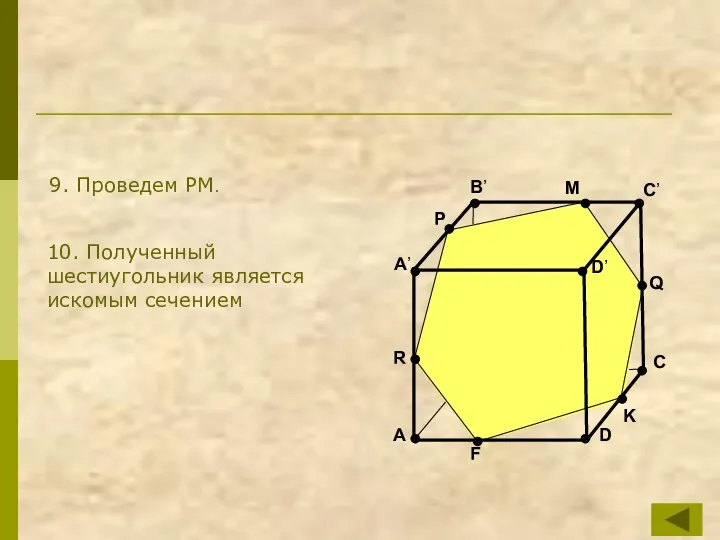
- 25. B A C D A’ B’ C’ D’ R P Q K F M 9. Проведем
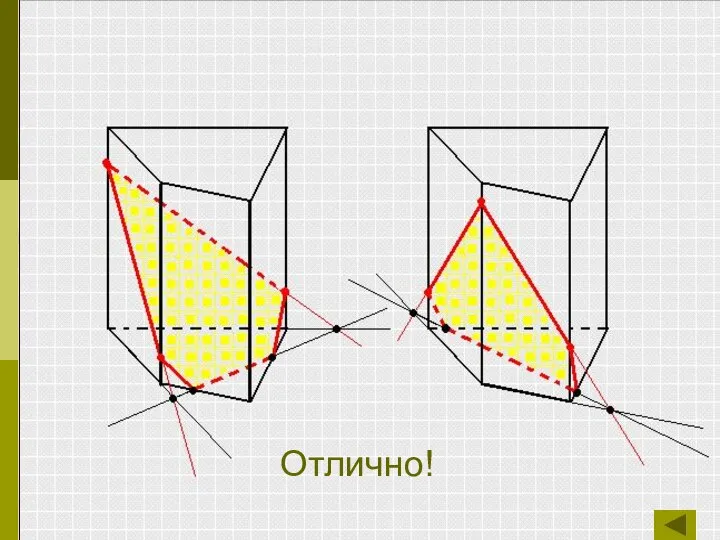
- 26. Задание № 4 Построй сечение куба, по трем данным точкам, а потом проверь себя, кликнув по
- 27. Защита проектов
- 28. Защита проектов Многоугольники, полученные при сечении куба Нахождение площади сечений многогранников
- 29. ТЕСТ Давайте, протестируемся Желаю удачи!
- 30. Отлично!
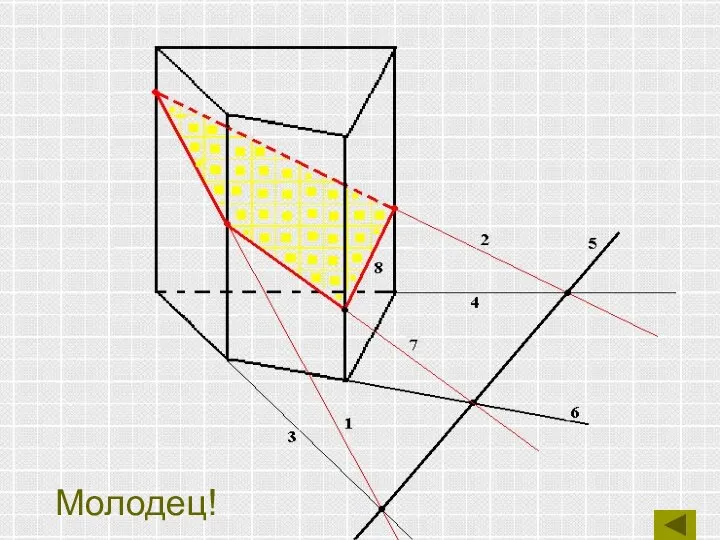
- 31. Молодец!
- 33. Скачать презентацию









 Способы решения квадратных уравнений
Способы решения квадратных уравнений Решение простейших тригонометрических уравнений. Подготовка к ЕГЭ
Решение простейших тригонометрических уравнений. Подготовка к ЕГЭ Частные производные
Частные производные Подготовка к ОГЭ, 9 класс, геометрия
Подготовка к ОГЭ, 9 класс, геометрия История возникновения числа ПИ
История возникновения числа ПИ Путешествие в страну Эколандию
Путешествие в страну Эколандию Путешествие в страну Математику
Путешествие в страну Математику Числовые выражения
Числовые выражения Использование циклов
Использование циклов Парусная регата. Деление десятичной дроби на натуральное число
Парусная регата. Деление десятичной дроби на натуральное число Решение задач
Решение задач Диаграммы. Задачи
Диаграммы. Задачи Волшебная страна - Геометрия. Занятие 3
Волшебная страна - Геометрия. Занятие 3 Основы тригонометрии. Радианная мера угла. Вращательное движение точки вокруг начла координат
Основы тригонометрии. Радианная мера угла. Вращательное движение точки вокруг начла координат Знакомство с образованием чисел второго десятка
Знакомство с образованием чисел второго десятка Оформление задач в 1 классе. Урок 2
Оформление задач в 1 классе. Урок 2 Распределение Максвелла
Распределение Максвелла Производная в электротехнике
Производная в электротехнике Касательные и секущие
Касательные и секущие Цифра в 21 веке
Цифра в 21 веке Комплeксные числа. Арифметические операции над ними (10 класс)
Комплeксные числа. Арифметические операции над ними (10 класс) Ур3
Ур3 Решение заданий олимпиады по математике
Решение заданий олимпиады по математике Сложение двух векторов
Сложение двух векторов Признаки подобия треугольников. Урок 31
Признаки подобия треугольников. Урок 31 Решение занимательных задач
Решение занимательных задач Треугольник
Треугольник Решение задач на применение признаков равенства треугольников. 7 класс
Решение задач на применение признаков равенства треугольников. 7 класс